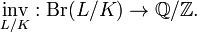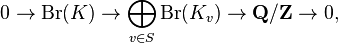Hasse invariant of an algebra

In mathematics, the Hasse invariant of an algebra is an invariant attached to a Brauer class of algebras over a field. The concept is named after Helmut Hasse. The invariant plays a role in local class field theory.

Local fields

Let K be a local field with valuation v and D a K-algebra. We may assume D is a division algebra with centre K of degree n. The valuation v can be extended to D, for example by extending it compatibly to each commutative subfield of D: the value group of this valuation is (1/n)Z.[1]

There is a commutative subfield L of D which is unramified over K, and D splits over L.[2] The field L is not unique but all such extensions are conjugate by the Skolem–Noether theorem, which further shows that any automorphism of L is induced by a conjugation in D. Take γ in D such that conjugation by γ induces the Frobenius automorphism of L/K and let v(γ) = k/n. Then k/n modulo 1 is the Hasse invariant of D. It depends only on the Brauer class of D.[3]

The Hasse invariant is thus a map defined on the Brauer group of a local field K to the divisible group Q/Z.[3][4] Every class in the Brauer group is represented by a class in the Brauer group of an unramified extension of L/K of degree n,[5] which by the Grunwald–Wang theorem and the Albert–Brauer–Hasse–Noether theorem we may take to be a cyclic algebra (L,φ,πk) for some k mod n, where φ is the Frobenius map and π is a uniformiser.[6] The invariant map attaches the element k/n mod 1 to the class. This exhibits the invariant map as a homomorphism

\underset{L/K}{\operatorname{inv}} : \operatorname{Br}(L/K) \rightarrow \mathbb{Q}/\mathbb{Z} .

The invariant map extends to Br(K) by representing each class by some element of Br(L/K) as above.[3][4]

For a non-Archimedean local field, the invariant map is a group isomorphism.[3][7]

In the case of the field R of real numbers, there are two Brauer classes, represented by the algebra R itself and the quaternion algebra H.[8] It is convenient to assign invariant zero to the class of R and invariant 1/2 modulo 1 to the quaternion class.

In the case of the field C of complex numbers, the only Brauer class is the trivial one, with invariant zero.[9]

Global fields

For a global field K, given a central simple algebra D over K then for each valuation v of K we can consider the extension of scalars Dv = D ⊗ Kv The extension Dv splits for all but finitely many v, so that the local invariant of Dv is almost always zero. The Brauer group Br(K) fits into an exact sequence[8][9]

0\rightarrow \textrm{Br}(K)\rightarrow \bigoplus_{v\in S} \textrm{Br}(K_v)\rightarrow \mathbf{Q}/\mathbf{Z} \rightarrow 0,

where S is the set of all valuations of K and the right arrow is the sum of the local invariants. The injectivity of the left arrow is the content of the Albert–Brauer–Hasse–Noether theorem. Exactness in the middle term is a deep fact from global class field theory.

References

  1. ↑ Serre (1967) p.137
  2. ↑ Serre (1967) pp.130,138
  3. 1 2 3 4 Serre (1967) p.138
  4. 1 2 Lorenz (2008) p.232
  5. ↑ Lorenz (2008) pp.225–226
  6. ↑ Lorenz (2008) p.226
  7. ↑ Lorenz (2008) p.233
  8. 1 2 Serre (1979) p.163
  9. 1 2 Gille & Szamuely (2006) p.159

Further reading

This article is issued from Wikipedia - version of the Sunday, June 28, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.