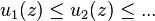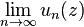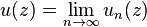Harnack's principle

In complex analysis, Harnack's principle or Harnack's theorem is one of several closely related theorems about the convergence of sequences of harmonic functions, that follow from Harnack's inequality.

If the functions 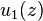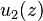$u_1(z)$ , $u_2(z)$ , ... are harmonic in an open connected subset $G$ of the complex plane C, and

u_1(z) \le u_2(z) \le ...

in every point of $G$ , then the limit

\lim_{n\to\infty}u_n(z)

either is infinite in every point of the domain $G$ or it is finite in every point of the domain, in both cases uniformly in each compact subset of $G$ . In the latter case, the function

u(z) = \lim_{n\to\infty}u_n(z)

is harmonic in the set $G$ .

References

Kamynin, L.I. (2001), "Harnack theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
This article incorporates material from Harnack's principle on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia - version of the Thursday, February 28, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.