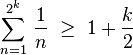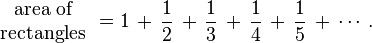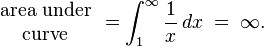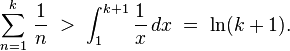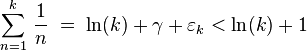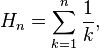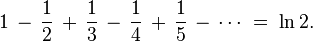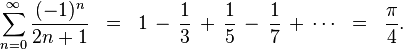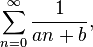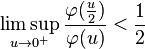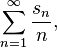Harmonic series (mathematics)
| Part of a series of articles about | ||||||
| Calculus | ||||||
|---|---|---|---|---|---|---|
|
||||||
|
Specialized |
||||||
In mathematics, the harmonic series is the divergent infinite series:
Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength. Every term of the series after the first is the harmonic mean of the neighboring terms; the phrase harmonic mean likewise derives from music.
History
The fact that the harmonic series diverges was first proven in the 14th century by Nicole Oresme,[1] but this achievement fell into obscurity. Proofs were given in the 17th century by Pietro Mengoli,[2] Johann Bernoulli,[3] and Jacob Bernoulli.[4]
Historically, harmonic sequences have had a certain popularity with architects. This was so particularly in the Baroque period, when architects used them to establish the proportions of floor plans, of elevations, and to establish harmonic relationships between both interior and exterior architectural details of churches and palaces.[5]
Paradoxes
The harmonic series is counterintuitive to students first encountering it, because it is a divergent series though the limit of the nth term as n goes to infinity is zero. The divergence of the harmonic series is also the source of some apparent paradoxes. One example of these is the "worm on the rubber band".[6] Suppose that a worm crawls along a 1-metre rubber band at the same time as the rubber band is uniformly stretched. If the worm travels 1 centimetre per minute and the band stretches 1 metre per minute, will the worm ever reach the end of the rubber band? The answer, counterintuitively, is "yes", for after n minutes, the ratio of the distance travelled by the worm to the total length of the rubber band is
(In fact the actual ratio is a little less than this sum as the band expands continuously). The reason is that the band expands behind the worm also; eventually, the worm gets past the midway mark and the band behind expands increasingly more rapidly than the band in front.
Because the series gets arbitrarily large as n becomes larger, eventually this ratio must exceed 1, which implies that the worm reaches the end of the rubber band. However, the value of n at which this occurs must be extremely large: approximately e100, a number exceeding 1043. Although the harmonic series does diverge, it does so very slowly.
Another problem involving the harmonic series is the Jeep problem.
Another example is: given a collection of identical dominoes, it is clearly possible to stack them at the edge of a table so that they hang over the edge of the table without falling. The counterintuitive result is that one can stack them in such a way as to make the overhang arbitrarily large, provided there are enough dominoes.[6][7]
A simpler example, on the other hand, is the swimmer that keeps adding more speed when touching the walls of the pool. The swimmer starts crossing a 10-meter pool at a speed of 2 m/s, and with every cross, another 2 m/s is added to the speed. In theory, the swimmer's speed is unlimited, but the number of pool crosses needed to get to that speed becomes very large; for instance, to get to the speed of light (ignoring special relativity), the swimmer needs to cross the pool 150 million times. Contrary to this large number, the "time" required to reach a given speed depends on the sum of the series at any given number of pool crosses (iterations):
Calculating the sum (iteratively) shows that to get to the speed of light the time required is only 94 seconds. By continuing beyond this point (exceeding the speed of light, again ignoring special relativity), the time taken to cross the pool will in fact approach zero as the number of iterations becomes very large, and although the time required to cross the pool appears to tend to zero (at an infinite number of iterations), the sum of iterations (time taken for total pool crosses) will still diverge at a very slow rate.
Divergence
There are several well-known proofs of the divergence of the harmonic series. A few of them are given below.
Comparison test
One way to prove divergence is to compare the harmonic series with another divergent series:
Each term of the harmonic series is greater than or equal to the corresponding term of the second series, and therefore the sum of the harmonic series must be greater than the sum of the second series. However, the sum of the second series is infinite:
It follows (by the comparison test) that the sum of the harmonic series must be infinite as well. More precisely, the comparison above proves that
This proof, proposed by Nicole Oresme, is considered by many in the mathematical community to be a high point of medieval mathematics. It is still a standard proof taught in mathematics classes today. Cauchy's condensation test is a generalization of this argument.
Integral test

It is possible to prove that the harmonic series diverges by comparing its sum with an improper integral. Specifically, consider the arrangement of rectangles shown in the figure to the right. Each rectangle is 1 unit wide and 1 / n units high, so the total area of the rectangles is the sum of the harmonic series:
However, the total area under the curve y = 1 / x from 1 to infinity is given by an improper integral:
Since this area is entirely contained within the rectangles, the total area of the rectangles must be infinite as well. More precisely, this proves that
The generalization of this argument is known as the integral test.
Rate of divergence
The harmonic series diverges very slowly. For example, the sum of the first 1043 terms is less than 100.[8] This is because the partial sums of the series have logarithmic growth. In particular,
where  is the Euler–Mascheroni constant and
is the Euler–Mascheroni constant and  which approaches 0 as
which approaches 0 as  goes to infinity. Leonhard Euler proved both this and also the more striking fact that the sum which includes only the reciprocals of primes also diverges, i.e.
goes to infinity. Leonhard Euler proved both this and also the more striking fact that the sum which includes only the reciprocals of primes also diverges, i.e.
Partial sums
The nth partial sum of the diverging harmonic series,
is called the nth harmonic number.
The difference between the nth harmonic number and the natural logarithm of n converges to the Euler–Mascheroni constant.
The difference between distinct harmonic numbers is never an integer.
No harmonic numbers are integers, except for n = 1.[9]
Related series
Alternating harmonic series
The series
is known as the alternating harmonic series. This series converges by the alternating series test. In particular, the sum is equal to the natural logarithm of 2:
This formula is a special case of the Mercator series, the Taylor series for the natural logarithm. A proof without words that the sum is 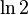 was shown by Matt Hudelson.[10]
was shown by Matt Hudelson.[10]
A related series can be derived from the Taylor series for the arctangent:
This is known as the Leibniz series.
General harmonic series
The general harmonic series is of the form
where  and
and  are real numbers.
are real numbers.
By the comparison test, all general harmonic series diverge.
p-series
A generalization of the harmonic series is the p-series (or hyperharmonic series), defined as
for any positive real number p. When p = 1, the p-series is the harmonic series, which diverges. Either the integral test or the Cauchy condensation test shows that the p-series converges for all p > 1 (in which case it is called the over-harmonic series) and diverges for all p ≤ 1. If p > 1 then the sum of the p-series is ζ(p), i.e., the Riemann zeta function evaluated at p.
The problem of finding the sum for p = 2 is called the Basel problem. The value of the sum for p = 3 is called Apéry's constant.
ln-series
Related to p-series is ln-series, defined as
for any positive real number p. This can be shown by integral test to diverge for p ≤ 1 but converge for all p > 1.
φ-series
For any convex, real-valued function φ such that
the series ∑n≥1 φ(n−1) is convergent.
Random harmonic series
The random harmonic series
where the sn are independent, identically distributed random variables taking the values +1 and −1 with equal probability 1/2, is a well-known example in probability theory for a series of random variables that converges with probability 1. The fact of this convergence is an easy consequence of either the Kolmogorov three-series theorem or of the closely related Kolmogorov maximal inequality. Byron Schmuland of the University of Alberta further examined[11][12] the properties of the random harmonic series, and showed that the convergent is a random variable with some interesting properties. In particular, the probability density function of this random variable evaluated at +2 or at −2 takes on the value 0.124999999999999999999999999999999999999999764…, differing from 1/8 by less than 10−42. Schmuland's paper explains why this probability is so close to, but not exactly, 1/8. The exact value of this probability is given by the infinite cosine product integral  [13] divided by π.
[13] divided by π.
Depleted harmonic series
The depleted harmonic series where all of the terms in which the digit 9 appears anywhere in the denominator are removed can be shown to converge and its value is less than 80.[14] In fact when terms containing any particular string of digits are removed the series converges.
See also
| Wikimedia Commons has media related to Harmonic series. |
References
- ↑ Nicole Oresme (ca. 1360) Quastiones super Geometriam Euclidis (Questions concerning Euclid's Geometry).
- ↑ Pietro Mengoli, Novæ quadraturæ arithmeticæ, seu De additione fractionum [New arithmetic quadrature (i.e., integration), or On the addition of fractions] (Bologna ("Bononiæ"), (Italy): Giacomo Monti ("Jacobi Monti"), 1650). The proof of the divergence of the harmonic series is presented in the book's preface (Præfatio).
Mengoli's proof is by contradiction:
Let S denote the sum of the series. Group the terms of the series in triplets:
S = 1 + (1/2 + 1/3 + 1/4) + (1/5 + 1/6 + 1/7) + (1/8 + 1/9 + 1/10) + …
Since for x > 1, 1/(x-1) + 1/x + 1/(x+1) > 3/x, then
S > 1 + (3/3) + (3/6) + (3/9) + … = 1 + 1 + 1/2 + 1/3 + … = 1 + S, which is false for any finite S. Therefore, the series diverges. - ↑ See: Corollary III of De seriebus varia in: Johannis Bernoulli, Opera Omnia (Lausanne & Basel, Switzerland: Marc-Michel Bousquet & Co., 1742), vol. 4, p. 8, Corollary III.
- ↑ See:
- Jacob Bernoulli, Propositiones arithmeticae de seriebus infinitis earumque summa finita [Arithmetical propositions about infinite series and their finite sums] (Basel, Switzerland: J. Conrad, 1689).
- Jacob Bernoulli, Ars conjectandi, opus posthumum. Accedit Tractatus de seriebus infinitis … [Theory of inference, posthumous work. With the "Treatise on infinite series" joined … ] (Basel, Switzerland: Thurneysen, 1713), pp. 250–251. From page 250, proposition 16:
"XVI. Summa serei infinita harmonicè progressionalium, 1/1 + 1/2 + 1/3 + 1/4 + 1/5 &c. est infinita.
- Id primus deprehendit Frater: … "
[My] brother first discovered it [i.e., this proof].) - ↑ George L. Hersey, Architecture and Geometry in the Age of the Baroque, p 11-12 and p37-51.
- 1 2 Graham, Ronald; Knuth, Donald E.; Patashnik, Oren (1989), Concrete Mathematics (2nd ed.), Addison-Wesley, pp. 258–264, ISBN 978-0-201-55802-9
- ↑ Sharp, R.T. (1954), "Problem 52: Overhanging dominoes" (PDF), Pi Mu Epsilon Journal 1 (10): 411–412
- ↑ "Sloane's A082912 : Sum of a(n) terms of harmonic series is > 10^n", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Harmonic Number". Wolfram Research, Inc. Retrieved November 20, 2014.
- ↑ Hudelson, Matt (1 October 2010). "Proof Without Words: The Alternating Harmonic Series Sums to ln 2" (PDF). Mathematics Magazine 83 (4): 294. doi:10.4169/002557010X521831.
- ↑ "Random Harmonic Series", American Mathematical Monthly 110, 407–416, May 2003
- ↑ Schmuland's preprint of Random Harmonic Series
- ↑ Weisstein, Eric W. “Infinite Cosine Product Integral.” From MathWorld – a Wolfram Web Resource. http://mathworld.wolfram.com/InfiniteCosineProductIntegral.html accessed 11/14/2010
- ↑ Nick's Mathematical Puzzles: Solution 72
External links
- Hazewinkel, Michiel, ed. (2001), "Harmonic series", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- "The Harmonic Series Diverges Again and Again", The AMATYC Review, 27 (2006), pp. 31–43. Many proofs of divergence of harmonic series.
- Weisstein, Eric W., "Harmonic Series", MathWorld.
- Weisstein, Eric W., "Book Stacking Problem", MathWorld.
| ||||||||||||||||||||||||||||||||||
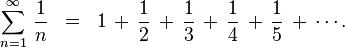
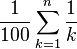
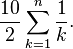
![\begin{align}
& 1 \;\;+\;\; \frac{1}{2} \;\;+\;\; \frac{1}{3} \,+\, \frac{1}{4} \;\;+\;\; \frac{1}{5} \,+\, \frac{1}{6} \,+\, \frac{1}{7} \,+\, \frac{1}{8} \;\;+\;\; \frac{1}{9} \,+\, \cdots \\[12pt]
>\;\;\; & 1 \;\;+\;\; \frac{1}{2} \;\;+\;\; \frac{1}{4} \,+\, \frac{1}{4} \;\;+\;\; \frac{1}{8} \,+\, \frac{1}{8} \,+\, \frac{1}{8} \,+\, \frac{1}{8} \;\;+\;\; \frac{1}{16} \,+\, \cdots
\end{align}](../I/m/b91977135fcc1776992e8ef056f5faeb.png)
![\begin{align}
& 1 + \left(\frac{1}{2}\right) + \left(\frac{1}{4}+\frac{1}{4}\right) + \left(\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8}\right) + \left(\frac{1}{16}+\cdots+\frac{1}{16}\right) + \cdots \\[12pt]
=\;\; & 1 \;\;+\;\; \frac{1}{2} \;\;+\;\; \frac{1}{2} \;\;+\;\; \frac{1}{2} \;\;+\;\; \frac{1}{2} \;\;+\;\; \cdots \;\;=\;\; \infty
\end{align}](../I/m/77c8fd72912263f0e70a4a7386a14c32.png)