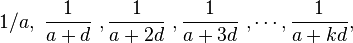Harmonic progression (mathematics)

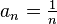 .
.In mathematics, a harmonic progression (or harmonic sequence) is a progression formed by taking the reciprocals of an arithmetic progression. In other words, it is a sequence of the form
where −a/d is not a natural number and k is a natural number.
(Terms in the form 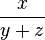 can be expressed as
can be expressed as 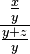 , we can let
, we can let 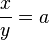 and
and 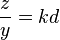 .)
.)
Equivalently, a sequence is a harmonic progression when each term is the harmonic mean of the neighboring terms.
It is not possible for a harmonic progression (other than the trivial case where a = 1 and k = 0) to sum to an integer. The reason is that, necessarily, at least one denominator of the progression will be divisible by a prime number that does not divide any other denominator.[1]
Examples
- 12, 6, 4, 3,
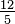 , 2, … ,
, 2, … , 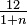
- 10, 30, −30, −10, −6, −
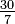 , … ,
, … , 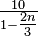
Use in geometry
If collinear points A, B, C, and D are such that D is the harmonic conjugate of C with respect to A and B, then the distances from any one of these points to the three remaining points form harmonic progression.[2][3] Specifically, each of the sequences AC, AB, AD; BC, BA, BD; CA, CD, CB; and DA, DC, DB are harmonic progressions, where each of the distances is signed according to a fixed orientation of the line.
See also
References
- ↑ Erdős, P. (1932), "Egy Kürschák-féle elemi számelméleti tétel általánosítása" [Generalization of an elementary number-theoretic theorem of Kürschák] (PDF), Mat. Fiz. Lapok (in Hungarian) 39: 17–24. As cited by Graham, Ronald L. (2013), "Paul Erdős and Egyptian fractions", Erdős centennial, Bolyai Soc. Math. Stud. 25, János Bolyai Math. Soc., Budapest, pp. 289–309, doi:10.1007/978-3-642-39286-3_9, MR 3203600.
- ↑ Chapters on the modern geometry of the point, line, and circle, Vol. II by Richard Townsend (1865) p. 24
- ↑ Modern geometry of the point, straight line, and circle: an elementary treatise by John Alexander Third (1898) p. 44
- Mastering Technical Mathematics by Stan Gibilisco, Norman H. Crowhurst, (2007) p. 221
- Standard mathematical tables by Chemical Rubber Company (1974) p. 102
- Essentials of algebra for secondary schools by Webster Wells (1897) p. 307