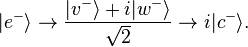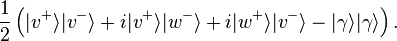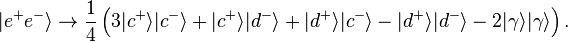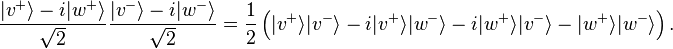Hardy's paradox

Hardy's paradox is a thought experiment in quantum mechanics devised by Lucien Hardy^[1]^[2] in 1992-3 in which a particle and its antiparticle may interact without annihilating each other.

Experiments^[3]^[4] using the technique of weak measurement^[5] have studied an interaction of polarized photons and these have demonstrated that the phenomenon does occur. However, the consequence of these experiments is only that past events can be inferred after their occurrence as a probabilistic wave collapse. These weak measurements are considered to be an observation themselves, and therefore part of the causation of wave collapse, making the objective results only a probabilistic function rather than a fixed reality. However, a careful analysis of the experiment shows that Hardy's paradox only proves that a local hidden variable theory can not exist, as there can not be a theory that assumes that the system meets the states of reality regardless of the interaction with the measuring apparatus. This confirms that a quantum theory, to be consistent with the experiments, must be non-local (in the sense of Bell) and contextual.

Setup description and the results

Setup for Hardy's thought experiment

The basic building block of Hardy’s thought experiment are two Mach–Zehnder interferometers for quantum particles and antiparticles. We will describe the case using electrons and positrons. Each interferometer consists of bent paths and two beam splitters (labeled BS¹ and BS² in the accompanying diagram) and is tuned so that when operating individually particles always exit to the same particle detector (the ones labeled "c" in the diagram – "c" is for "constructive interference" and "d" is for "destructive interference"). For example, for the right-hand side interferometer, when operating alone, entering electrons (labeled e⁻) become a quantum superposition of electrons taking the path v⁻ and electrons taking path w⁻ (in the diagram, the latter part of the w path is labeled u⁻), but these constructively interfere and thus always exit in arm c⁻:

| e^{-} \rangle \to \frac{|v^{-}\rangle + i |w^{-}\rangle}{\sqrt{2}} \to i |c^{-} \rangle.

Similarly, positrons (labeled e⁺) are always detected at c⁺. In the actual experiment the interferometers are arranged so that part of their paths overlap as shown in the diagram. If the amplitude for the particle in one arm, say w⁻, were to be obstructed by a second particle in w⁺ that collides with it, only the v amplitude would reach the second beam splitter, and would split into arms c⁺ and d⁺ with equal amplitude. The detection of a particle in d⁺ would thus indicate the presence of the obstructing particle, but without an annihilation taking place. For this reason, this scheme was named interaction-free measurement.

If (classically speaking) both the electron and the positron take the w paths in their respective interferometers, they will annihilate to produce two gamma rays: 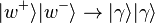$| w^{+} \rangle | w^{-} \rangle \to | \gamma \rangle| \gamma \rangle$ . There is a 1 in 4 chance of this happening. We can express the state of the system, before the final beam splitters, as

\frac 1 2\left(|v^{+}\rangle|v^{-}\rangle + i |v^{+}\rangle|w^{-}\rangle+i|w^{+}\rangle|v^{-}\rangle-|\gamma\rangle|\gamma\rangle\right).

Since the c detectors click for 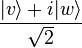$\frac{|v\rangle + i |w\rangle}{\sqrt{2}}$ and the d detectors for 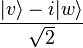$\frac{|v\rangle - i |w\rangle}{\sqrt{2}}$ , this becomes:

| e^{+} e^{-} \rangle \to \frac14 \left(3|c^{+} \rangle |c^{-} \rangle +|c^{+} \rangle |d^{-} \rangle + |d^{+} \rangle |c^{-} \rangle - |d^{+} \rangle |d^{-} \rangle - 2| \gamma \rangle| \gamma \rangle \right).

Since the probabilities are the squares of the absolute values of these amplitudes, this means a 9 in 16 chance of each particle being detected in its respective c detector, a 1 in 16 chance for one particle being detected in its c detector and the other in its d detector, or for both being detected in their d detectors, and a 4 in 16 (1 in 4) chance that the electron and positron annihilate so neither is detected. Notice that a detection in both d detectors is represented by

\frac{|v^{+}\rangle - i |w^{+}\rangle}{\sqrt{2}} \frac{|v^{-}\rangle - i |w^{-}\rangle}{\sqrt{2}}= \frac 1 2\left(|v^{+}\rangle|v^{-}\rangle - i |v^{+}\rangle|w^{-}\rangle-i|w^{+}\rangle|v^{-}\rangle-|w^{+}\rangle|w^{-}\rangle\right).

This is not orthogonal to the expression above for the state before the final beam splitters. The scalar product between them is 1/4, showing that there is a 1 in 16 chance of this happening, paradoxically.

The situation can be analyzed in terms of two simultaneous interaction-free measurements: from the point of view of the interferometer on the left, a click at d⁺ implies the presence of the obstructing electron in u⁻. Similarly, for the interferometer on the right, a click at d⁻ implies the presence of the positron in u⁺. Indeed, every time a click is recordered at d⁺ (or d⁻) the other particle is found in u⁻ (or u⁺, resp.). If we assume the particles are independent (described by local hidden variables), we conclude that they can never emerge simultaneously in d⁺ and d⁻. This would imply that they were in u⁺ and u⁻, which cannot occur because of the annihilation process.

A paradox then arises because sometimes the particles do emerge simultaneously at d⁺ and d⁻ (with probability p=1/16). Quantum mechanically, the 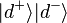$|d^{+} \rangle | d^{-} \rangle$ term arises, in fact, from the nonmaximally entangled nature of the state just before the final beam splitters.

A paper by Yakir Aharonov and colleagues in 2001^[6] pointed out that the number of electrons or positrons in each branch is theoretically observable, and is 0 in the w branches and 1 in the v branches. And yet, the number of electron-positron pairs in any combination is also observable, and is not given by the product of the single-particle values. So we find that the number of ww pairs (both particles in their w path) is 0, each wv pair is 1, and the number in the vv combination is −1! They proposed a way that this could be observed physically by temporarily trapping the electron and the positron in the v paths in boxes and noting the effect of their mutual electrostatic attraction. They stated that one would actually find a repulsion between the boxes.

In 2009 Jeff Lundeen and Aephraim Steinberg published work^[3] in which they set up a "Hardy's paradox" system using photons. A 405 nm laser goes through a barium borate crystal to produce pairs of 810 nm photons, with polarizations orthogonal one to the other. These then hit a beam splitter, which sends photons back to the barium borate crystal with 50% probability. The 405 nm pumping beam also bounces off a mirror and comes back to the barium borate. If both the 810 nm photons come back to the crystal, they are annihilated by interaction with the returning pump beam. In any case, the beam of photons that make it through the crystal and the beam of photons that pass through the beam splitter are both separated into "vertically polarized" and "horizontally polarized" beams, which correspond to the "electrons" and the "positrons" of Hardy's scheme. The two "electron" beams (the photons with one kind of polarization) are united at a beam splitter and go to one or two detectors, and the same for the "positrons" (the other photons). Classically, no photons should be detected at what the authors call the "dark ports" because if they take both directions from the first beam splitter, they will interfere with themselves, whereas if they take only one path, then one cannot detect them both at the dark ports because of the paradox. By introducing a 20° rotation in polarization and using half-wave plates on certain beams, and then measuring coincidence rates at the detectors, they were able to make weak measurements that allowed them to calculate the "occupation" of different arms (paths) and combinations. As predicted by Aharonov and colleagues, they found a negative value for the combination in which both photons take the outer (no-annihilation) route. The results were not exactly as predicted and they attribute this to imperfect switching (annihilation) and interaction-free measurements.

References

↑ Hardy, Lucien (1992). "Quantum mechanics, local realistic theories, and Lorentz-invariant realistic theories". Physical Review Letters 68 (20): 2981–2984. Bibcode:1992PhRvL..68.2981H. doi:10.1103/PhysRevLett.68.2981. PMID 10045577.
↑ Hardy, Lucien (1993). "Nonlocality for two particles without inequalities for almost all entangled states". Physical Review Letters 71 (11): 1665–1668. Bibcode:1993PhRvL..71.1665H. doi:10.1103/PhysRevLett.71.1665. PMID 10054467.
1 2 Lundeen, J. S.; Steinberg, A. M. (2009). "Experimental Joint Weak Measurement on a Photon Pair as a Probe of Hardy's Paradox". Physical Review Letters 102 (2): 020404–000001. arXiv:0810.4229. Bibcode:2009PhRvL.102b0404L. doi:10.1103/PhysRevLett.102.020404. . Also available here.
↑ Yokota, K.; Yamamoto, T.; Koashi, M.; Imoto, N. (2009). "Direct observation of Hardy's paradox by joint weak measurement with an entangled photon pair". New Journal of Physics 11 (3): 033011. arXiv:0811.1625. Bibcode:2009NJPh...11c3011Y. doi:10.1088/1367-2630/11/3/033011.
↑ Y. Aharonov, D.Z. Albert, L. Vaidman, "How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100," Physical Review Letters, 1988.
↑ Revisiting Hardy’s Paradox: Counterfactual Statements, Real Measurements, Entanglement and Weak Values, by Yakir Aharonov et al., 2001.

External links

Lecture by Aephraim Steinberg, 2012

Hardy's paradox

Setup description and the results

References

External links

See also