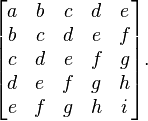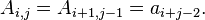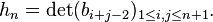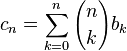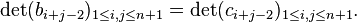Hankel matrix
In linear algebra, a Hankel matrix (or catalecticant matrix), named after Hermann Hankel, is a square matrix in which each ascending skew-diagonal from left to right is constant, e.g.:
Any n×n matrix A of the form

is a Hankel matrix. If the i,j element of A is denoted Ai,j, then we have
The Hankel matrix is closely related to the Toeplitz matrix (a Hankel matrix is an upside-down Toeplitz matrix). For a special case of this matrix see Hilbert matrix.
A Hankel operator on a Hilbert space is one whose matrix with respect to an orthonormal basis is a (possibly infinite) Hankel matrix
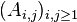 , where
, where  depends only on
depends only on  .
.
The determinant of a Hankel matrix is called a catalecticant.
Hankel transform
The Hankel transform is the name sometimes given to the transformation of a sequence, where the transformed sequence corresponds to the determinant of the Hankel matrix. That is, the sequence  is the Hankel transform of the sequence
is the Hankel transform of the sequence  when
when
Here, 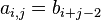 is the Hankel matrix of the sequence
is the Hankel matrix of the sequence 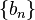 . The Hankel transform is invariant under the binomial transform of a sequence. That is, if one writes
. The Hankel transform is invariant under the binomial transform of a sequence. That is, if one writes
as the binomial transform of the sequence 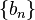 , then one has
, then one has
Hankel matrices for system identification
Hankel matrices are formed when, given a sequence of output data, a realization of an underlying state-space or hidden Markov model is desired. The singular value decomposition of the Hankel matrix provides a means of computing the A, B, and C matrices which define the state-space realization.
Orthogonal polynomials on the real line
Positive Hankel matrices and the Hamburger moment problems
Relation between Hankel and Toeplitz matrices
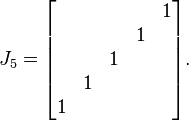
Let  be the reflection matrix of order
be the reflection matrix of order  .
For example the reflection matrix of order
.
For example the reflection matrix of order 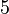 is as follows:
is as follows:
If 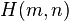 is a
is a 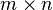 Hankel matrix, then
Hankel matrix, then
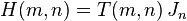 , where
, where 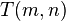 is a
is a 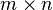 Toeplitz matrix.
Toeplitz matrix.
See also
- Cauchy matrix
- Vandermonde matrix
- Displacement rank
Notes
References
- Brent R.P. (1999), "Stability of fast algorithms for structured linear systems", Fast Reliable Algorithms for Matrices with Structure (editors—T. Kailath, A.H. Sayed), ch.4 (SIAM).
- Victor Y. Pan (2001). Structured matrices and polynomials: unified superfast algorithms. Birkhäuser. ISBN 0817642404.
- J.R. Partington (1988). An introduction to Hankel operators. LMS Student Texts 13. Cambridge University Press. ISBN 0-521-36791-3.