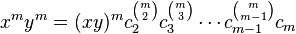Hall–Petresco identity

In mathematics, the Hall–Petresco identity (sometimes misspelled Hall–Petrescu identity) is an identity holding in any group. It was introduced by Hall (1934) and Petresco (1954). It can be proved using the commutator collecting process, and implies that p-groups of small class are regular.

Statement

The Hall–Petresco identity states that if x and y are elements of a group G and m is a positive integer then

x^my^m=(xy)^mc_2^{\binom{m}{2}}c_3^{\binom{m}{3}}\cdots c_{m-1}^{\binom{m}{m-1}}c_m

where each c_i is in the subgroup K_i of the descending central series of G.

References

Hall, Marshall (1959), The theory of groups, Macmillan, MR 0103215
Hall, Philip (1934), "A contribution to the theory of groups of prime-power order", Proceedings of the London Mathematical Society 36: 29–95, doi:10.1112/plms/s2-36.1.29
Huppert, B. (1967), Endliche Gruppen (in German), Berlin, New York: Springer-Verlag, pp. 90–93, ISBN 978-3-540-03825-2, MR 0224703, OCLC 527050
Petresco, Julian (1954), "Sur les commutateurs", Mathematische Zeitschrift 61 (1): 348–356, doi:10.1007/BF01181351, MR 0066380

This article is issued from Wikipedia - version of the Sunday, March 29, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.