Dipole antenna


| Part of a series on |
| Antennas |
|---|
 |
|
Common types |
|
Radiation sources / regions |

In radio and telecommunications a dipole antenna or doublet[1] is the simplest and most widely used class of antenna.[2][3] It consists of two identical conductive elements[4] such as metal wires or rods, which are usually bilaterally symmetrical.[3][5][6] The driving current from the transmitter is applied, or for receiving antennas the output signal to the receiver is taken, between the two halves of the antenna. Each side of the feedline to the transmitter or receiver is connected to one of the conductors. This contrasts with a monopole antenna, which consists of a single rod or conductor with one side of the feedline connected to it, and the other side connected to some type of ground.[6] A common example of a dipole is the "rabbit ears" television antenna found on broadcast television sets.
The most common form of dipole is two straight rods or wires oriented end to end on the same axis, with the feedline connected to the two adjacent ends. This is the simplest type of antenna from a theoretical point of view.[1] Dipoles are resonant antennas, meaning that the elements serve as resonators, with standing waves of radio current flowing back and forth between their ends. So the length of the dipole elements is determined by the wavelength of the radio waves used.[3] The most common form is the half-wave dipole, in which each of the two rod elements is approximately 1/4 wavelength long, so the whole antenna is a half-wavelength long. The radiation pattern of a vertical dipole is omnidirectional; it radiates equal power in all azimuthal directions perpendicular to the axis of the antenna. For a half-wave dipole the radiation is maximum, 2.15 dBi perpendicular to the antenna axis, falling monotonically with elevation angle to zero on the axis, off the ends of the antenna.[7]
Several different variations of the dipole are also used, such as the folded dipole, short dipole, cage dipole, bow-tie, and batwing antenna. Dipoles may be used as standalone antennas themselves, but they are also employed as feed antennas (driven elements) in many more complex antenna types,[3][4] such as the Yagi antenna, parabolic antenna, reflective array, turnstile antenna, log periodic antenna, and phased array. The dipole was the earliest type of antenna; it was invented by German physicist Heinrich Hertz around 1886 in his pioneering investigations of radio waves.
Dipole characteristics
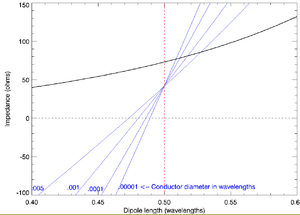
Impedance of dipoles of various lengths


The feedpoint impedance of a dipole antenna is very sensitive to its electrical length. Therefore a dipole will generally only perform optimally over a rather narrow bandwidth, beyond which its impedance will become a poor match for the transmitter or receiver (and transmission line). The real (resistive) and imaginary (reactive) components of that impedance, as a function of electrical length, are shown in the accompanying graph. The detailed calculation of these numbers are described below. Note that the value of the reactance is highly dependent on the diameter of the conductors; this plot is for conductors with a diameter of .001 wavelengths.
Dipoles that are much smaller than the wavelength of the signal are called short dipoles. These have a very low radiation resistance (and a high capacitive reactance) making them inefficient antennas. More of a transmitter's current is dissipated as heat due to the finite resistance of the conductors which is greater than the radiation resistance. However they can nevertheless be practical receiving antennas for longer wavelengths.[8]
Dipoles whose length is approximately half the wavelength of the signal are called half-wave dipoles and are widely used as such or as the basis for derivative antenna designs. These have a radiation resistance which is much greater, closer to the characteristic impedances of available transmission lines, and normally much larger than the resistance of the conductors, so that their efficiency approaches 100%. In general radio engineering, the term dipole, if not further qualified, is taken to mean a center-fed half-wave dipole.
A true half-wave dipole is one half of the wavelength λ in length, where λ=c/f in free space. Such a dipole has a feedpoint impedance consisting of 73Ω resistance and +43Ω reactance, thus presenting a slightly inductive reactance. In order to cancel that reactance, and present a pure resistance to the feedline, the element is shortened by the factor k for a net length l of:
where λ is the free-space wavelength, c is the speed of light, and f is the frequency. The adjustment factor k, in order for the reactance to be cancelled, depends on the diameter of the conductor.[9] For thin wires (diameter= 0.00001 wavelengths), k is approximately 0.98; for thick conductors (diameter= 0.008 wavelengths), k drops to about 0.94. This is because the effect of antenna length on reactance is much greater for thinner conductors. For the same reason, antennas with thicker conductors have a wider operating bandwidth over which they attain an acceptable standing wave ratio.
For a typical k of about .95, the above formula is often written for a length in metres of 143/f or a length in feet of 468/f where f is the frequency in megahertz.[10]
Dipole antennas of lengths approximately equal to any odd multiple of λ/2 are also resonant, presenting a small reactance (which can be cancelled by a small length adjustment). However these are rarely used. One size that is more practical though is a dipole with a length of 5/4 wavelengths. Not being close to 3/2 wavelengths, this antenna's impedance has a large (negative) reactance and can only be used with an impedance matching network (or "antenna tuner"). It is a desirable length because such an antenna has the highest gain for any dipole which isn't a great deal longer.
Radiation pattern and gain




(top) In linear scale
(bottom) In decibels isotropic (dBi)
A bare dipole is not considered a directional antenna. However like all antennas, its radiation is not uniform in all directions. Its radiation pattern in three dimensions is shaped like a toroid (doughnut) symmetric about the axis of the dipole. The radiation is maximum at right angles to the dipole, dropping off to zero on the antenna's axis. Therefore a dipole mounted vertically will be omnidirectional in the horizontal plane, with a modest gain, at the expense of radiation in the vertical direction.
Dipoles mounted horizontally (as is more common) will have gain in two opposing horizontal directions but nodes (directions of zero gain) at 90° from those directions (along the direction of the conductor). Neglecting electrical inefficiency, the antenna gain is equal to the directive gain, which is 1.5 or 1.76 dBi for a short dipole, increasing to 1.64 or 2.15 dBi for a half-wave dipole. For a 5/4 wave dipole the gain further increases to about 5.2 dBi, making this length desirable for that reason even though the antenna is then off-resonance. Longer dipoles than that have radiation patterns that are multi-lobed, with poorer gain (unless they are much longer) even along the strongest lobe. Other enhancements to the dipole (such as including a corner reflector or an array of dipoles) can be considered when more substantial directivity is desired. Such antenna designs, although based on the half-wave dipole, generally acquire their own names.
Feeding a dipole antenna
Ideally, a half-wave dipole should be fed using a balanced transmission line matching its typical 65 - 70Ω input impedance. Twin lead with a similar impedance is available but seldom used.
Many types of coaxial cable have a characteristic impedance of 75Ω, which would therefore be a good match for a half-wave dipole, however coax is an unbalanced transmission line (with one terminal at ground potential) whereas a dipole antenna presents a balanced input (both terminals have an equal but opposite voltage with respect to ground). When a balanced antenna is fed with a single-ended line, common mode currents can cause the coax line to radiate in addition to the antenna itself,[11] distorting the radiation pattern and changing the impedance seen by the line. The dipole can be properly fed, and retain its expected characteristics, by using a balun in between the coaxial feedline and the antenna terminals. Connection of coax to a dipole antenna using a balun is described in greater detail below.
Another solution, especially for receiving antennas, is to use common 300 ohm twin lead in conjunction with a folded dipole. The folded dipole is similar to the simple half-wave dipole but with the feedpoint impedance multiplied by 4, thus closely matching that 300 ohm impedance.[12] This is the most common household antenna for fixed FM broadcast band tuners, which usually include balanced 300 ohm antenna input terminals.
Dipole types
Short dipole

A short dipole is a physically feasible dipole formed by two conductors with a total length L substantially less than a half wavelength λ/2. As that length is reduced, the quantitative statements below become exact.
The feedpoint is usually at the center of the dipole. The current profile in each element, actually the tail end of a sinusoidal standing wave, is approximately a triangular distribution declining from the feedpoint current to zero at the ends. The far field electric field pattern at a distance r in the direction θ from the antenna's axis, is in the θ direction (transverse to the wave direction, in the plane of the antenna) of magnitude:
where ω is the radian frequency (ω=2πf) and k is the wavenumber (k=2π/λ). c is the speed of light, and the feedpoint current is assumed to be  .
.

This radiation pattern is similar to and only slightly less directional than that of the half-wave dipole.
Using the above expression for the radiation in the far field for a given feedpoint current, we can integrate over all solid angle to obtain the total radiated power.
where Z0 is the impedance of free space, Z0 = 1/(cε0).
From that, it is possible to infer the radiation resistance, equal to the resistive (real) part of the feedpoint impedance, neglecting a component due to ohmic losses. By setting Ptotal to the power supplied at the feedpoint  (since I0 is the peak current) we find:
(since I0 is the peak current) we find:
Again, these relationships are accurate for L<< λ/2. Setting L=λ/2 regardless, this formula would predict a radiation resistance of 49Ω, rather than the actual 73Ω value applying to the half-wave dipole.
Half-wave dipole
A half-wave dipole antenna consists of two quarter-wavelength conductors placed end to end for a total length of approximately L = λ/2.
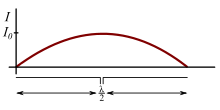

The current distribution is that of a standing wave, approximately sinusoidal along the length of the dipole, with a node at each end and an antinode (peak current) at the center (feedpoint):[13]
where k = 2π/λ and z runs from −L /2 to L /2.
In the far field, this produces a radiation pattern whose electric field is given by[13]
The directional factor cos[(π/2)cos θ]/sin θ is barely different from sin θ applying to the short dipole, resulting in a very similar radiation pattern as noted above.[13]
A numerical integration of this integral over all solid angle, as we did for the short dipole, supplies a value for the radiation resistance:
 Using the induced EMF method, the real part of the driving point impedance can also be written in terms of the cosine integral:
Using the induced EMF method, the real part of the driving point impedance can also be written in terms of the cosine integral:

If the dipole is not driven at the center, then the feed point resistance will be higher. If the feed point is distance x from one end of a half wave (λ/2) dipole, the radiation resistance relative to the feedpoint will be given by the following equation.
Comparing the radiated power at θ=0 to the total power found by integrating, we find the directive gain to be 1.64. This can also be directly computed using the cosine integral:
 (2.15 dBi)
(2.15 dBi)
| Gain of dipole antennas | ||
length L in  |
Gain | Gain(dBi) |
 0.5 0.5 |
1.50 | 1.76 |
| 0.5 | 1.64 | 2.15 |
| 1.25 | 3.3 | 5.2 |
Quarter-wave monopole

The quarter-wave monopole antenna is a single-element antenna fed at one end, that behaves as a dipole antenna. It is formed by a conductor  in length, fed in the lower end, which is near a conductive surface which works as a reflector (see effect of ground) and is an example of a Marconi antenna. The current in the reflected image has the same direction and phase as the current in the real antenna. The quarter-wave conductor and its image together form a half-wave dipole that radiates only in the upper half of space.
in length, fed in the lower end, which is near a conductive surface which works as a reflector (see effect of ground) and is an example of a Marconi antenna. The current in the reflected image has the same direction and phase as the current in the real antenna. The quarter-wave conductor and its image together form a half-wave dipole that radiates only in the upper half of space.
In this upper side of space, the emitted field has the same amplitude of the field radiated by a half-wave dipole fed with the same current. Therefore, the total emitted power is half the emitted power of a half-wave dipole fed with the same current. As the current is the same, the radiation resistance (real part of series impedance) will be half of the series impedance of a half-wave dipole. As the reactive part is also divided by 2, the impedance of a quarter-wave antenna is 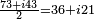 ohms. Since the fields above ground are the same as for the dipole, but only half the power is applied, the gain is twice (3 dB over) that of a half-wave dipole (
ohms. Since the fields above ground are the same as for the dipole, but only half the power is applied, the gain is twice (3 dB over) that of a half-wave dipole ( ), that is, 5.14 dBi.
), that is, 5.14 dBi.
The earth can be used as ground plane, but it is a poor conductor. The reflected antenna image is only clear at glancing angles (far from the antenna). At these glancing angles, electromagnetic fields and radiation patterns are the same as for a half-wave dipole. Naturally, the impedance of the earth is far inferior to that of a good conductor ground plane. This can be improved (at cost) by laying a copper mesh.
When the ground is not available (such as in a vehicle) other metallic surfaces can serve as a ground plane (typically the vehicle's roof). Alternatively, radial wires placed at the base of the antenna can form a ground plane. For VHF and UHF bands, the radiating and ground plane elements can be constructed from rigid rods or tubes. For a simple 1/4-wave whip, the radials are often sloped at a 45 degree angle to bring the feed point impedance closer to 50 ohms. Since this will introduce RF energy on the shield of the unbalanced feed line which deforms the radiation pattern of the antenna, a choke is often placed near the feed point.
Folded dipole

A folded dipole is a half-wave dipole with an additional wire connecting its two ends. If the additional wire has the same diameter and cross-section as the dipole, two nearly identical radiating currents are generated. The resulting far-field emission pattern is nearly identical to the one for the single-wire dipole described above, but at resonance its feedpoint impedance 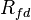 is four times the radiation resistance of a single-wire dipole. This is because for a fixed amount of power, the total radiating current
is four times the radiation resistance of a single-wire dipole. This is because for a fixed amount of power, the total radiating current  is equal to twice the current in each wire and thus equal to twice the current at the feed point. Equating the average radiated power to the average power delivered at the feedpoint, we may write
is equal to twice the current in each wire and thus equal to twice the current at the feed point. Equating the average radiated power to the average power delivered at the feedpoint, we may write
It follows that
The folded dipole is therefore well matched to 300-ohm balanced transmission lines. The folded dipole has a wider bandwidth than a single dipole. They can be used for transforming the value of input impedance of the dipole over a broad range of step-up ratios by changing the thicknesses of the wire conductors for the fed- and folded-sides.[14] Half wave folded dipoles are often used for FM radio antennas; versions made with twin lead which can be hung on an inside wall often come with FM tuners. The T2FD antenna is a folded dipole. They are also widely used as driven elements for rooftop Yagi television antennas.
Other dipole antenna types
There are numerous notable variations of dipole antennas:
- The bow-tie antenna is a dipole with flaring, triangular shaped arms. The shape gives it a much wider bandwidth than an ordinary dipole. It is widely used in UHF television antennas.
- The vee or quadrant antenna is a horizontal dipole with its arms at an angle instead of parallel. Quadrant antennas are notable in that they can be used to make horizontally polarized antennas with near-omnidirectional radiation patterns. They are used for broadcasting on the HF band.
- The G5RV Antenna is a dipole antenna with a symmetric feeder line, which also serves as a 1:1 impedance transformer allowing the transceiver to see the impedance of the antenna (it does not match the antenna to the 50-ohm transceiver. In fact the impedance will be somewhere around 90 ohms at the resonant frequency but significantly different at other frequencies).
- The sloper antenna is a slanted dipole antenna used for long-range communications or in limited space.
- The AS-2259 Antenna is an inverted-V dipole antenna used for NVIS communications.
Common applications
Set-top TV antenna

One of the most common applications of the dipole antenna is the rabbit ears or bunny ears television antenna, found atop broadcast television receivers. It is used to receive the VHF terrestrial television bands consisting of 52 to 88 MHz (band I) and 174 to 216 MHz (band III), with wavelengths of 5.5 to 1.4 m. Since this frequency range is much wider than a single fixed dipole antenna can cover, it is made with several degrees of adjustment. It is constructed of two telescoping rods that can be extended out to about 1 m length (approximately one quarter wavelength at 52 MHz). Instead of being fixed in opposing directions, these elements can be adjusted at an angle in a "V" shape. The reason for the V shape is that when receiving channels at the top of the band, the antenna elements will typically resonate at their 3rd harmonic. In this mode the direction of maximum gain is no longer perpendicular to the rods, but the radiation pattern will have lobes at an angle to the rods, making it advantageous to be able to adjust them to various angles.
FM broadcast receiving antennas
In contrast to the wide television frequency bands, the FM broadcast band (88-108 MHz) is narrow enough that a dipole antenna can cover it. For fixed use in homes, hi-fi tuners are typically supplied with simple folded dipoles resonant near the center of that band. The feedpoint impedance of a folded dipole, which is quadruple the impedance of a simple dipole, is a good match for 300Ω twin lead, so that is usually used for the transmission line to the tuner. A common construction is to make the arms of the folded dipole out of twin lead also, shorted at their ends. This flexible antenna can be conveniently taped or nailed to walls, following the contours of mouldings.
Shortwave antenna
Horizontal wire dipole antennas are popular for use on the HF shortwave bands, both for transmitting and shortwave listening. They are usually constructed of two lengths of wire joined by a strain insulator in the center, which is the feedpoint. The ends can be attached to existing buildings, structures, or trees, taking advantage of their heights. If used for transmitting, it is essential that the ends of the antenna be attached to supports through strain insulators with a sufficiently high flashover voltage, since the antenna's high voltage antinodes occur there. Being a balanced antenna, they are best fed with a balun in between the (coax) transmission line and the feedpoint.
These are simple to put up for temporary or field use. But they are also widely used by radio amateurs and short wave listeners in fixed locations due to their simple (and inexpensive) construction, while still realizing a resonant antenna at frequencies where resonant antenna elements need to be of quite some size. They are an attractive solution for these frequencies when significant directionality is not desired, and the cost of several such resonant antennas for different frequency bands, built at home, may still be much less than a single commercially produced antenna.
Dipole towers
Although the mast radiator antenna towers for MF and LF transmission are usually constructed as monopoles, some are dipoles. The metal structure of the mast is divided in half, and is driven in the center.
Dipole arrays
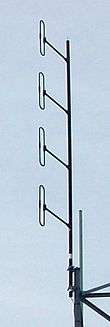
The dipole is a basic antenna element on the basis of which a driven array can be realized. The feedline is split using an electrical network in order to feed a number of elements, with careful attention paid to the relative phase delays due to transmission between the common point and each element. Putting dipoles into an array is used to increase the directional gain of the resulting array beyond the small gain of a single dipole element.
For a vertically oriented dipole, which is omnidirectional in the horizontal plane, it is possible to stack dipoles end-to-end, creating a collinear antenna array. That increases the gain at angles closer to the horizon at the expense of higher angles towards the sky. This is usually desired at higher frequencies (and anyway, stacking half-wave antennas end to end at lower frequencies would result in an impractical height). Collinear arrays are a thus a practical and higher gain alternative to quarter wave ground plane antennas used for VHF or UHF fixed base stations for mobile two-way radios, such as police, fire, and taxi dispatchers.

On the other hand, an array of dipoles can be used to realize substantial directivity in a particular horizontal direction. In a broadside array the dipoles can again be arranged colinear (end to end), or side by side, or both. The antennas are then fed in the same phase. This creates greater gain in the direction perpendicular to the antennas, at the expense of most other directions. Unfortunately that also means that the direction opposite the desired direction also has a high gain, whereas high gain is usually desired in one single direction. The power which is wasted in the reverse direction, however, can be recovered using a large planer reflector, as is accomplished in the reflective array antenna, increasing the gain in the desired direction by another 3 dB
This large reflector can be avoided in the end-fire array. In this case the dipoles are again side by side, but are fed in different phases. Rather than being directive perpendicular to the line connecting their feedpoints, now the directivity is along the line connecting their feedpoints. By using an appropriate spacing and phasing, the radiation can be directed in a single direction along that line, with radiation mainly cancelled in the reverse direction as well as most other directions.
Driven arrays of this sort require a complex system of signal splitting, phasing, distribution to the elements, and impedance matching. A different sort of end-fire array which is much more often used is based on the use of so-called parasitic elements. In the popular high-gain Yagi antenna, only one of the dipoles is actually connected electrically, but the others receive and reradiate power supplied by the driven element. This time, the phasing is accomplished by careful choice of the lengths as well as positions of the parasitic elements, in order to concentrate gain in one direction and largely cancel radiation in the opposite direction (as well as all other directions). Although the realized gain is less than a driven array with the same number of elements, the simplicity of the electrical connections makes the Yagi more practical for consumer applications.
Hertzian dipole

The Hertzian dipole or Elementary doublet refers to a theoretical construction, rather than a physical antenna design. It may be defined as a finite oscillating current (in a specified direction) of  over a tiny or infinitesimal length δℓ at a specified position. The solution of the fields from a Hertzian dipole can be used as the basis for analytical or numerical calculation of the radiation from more complex antenna geometries (such as practical dipoles) by forming the superposition of fields from a large number Hertzian dipoles comprising the current pattern of the actual antenna. As a function of position, taking the elementary current elements multiplied by infinitesimal lengths I(r)dℓ, the resulting field pattern then reduces to an integral over the path of an antenna conductor (modelled as a thin wire).
over a tiny or infinitesimal length δℓ at a specified position. The solution of the fields from a Hertzian dipole can be used as the basis for analytical or numerical calculation of the radiation from more complex antenna geometries (such as practical dipoles) by forming the superposition of fields from a large number Hertzian dipoles comprising the current pattern of the actual antenna. As a function of position, taking the elementary current elements multiplied by infinitesimal lengths I(r)dℓ, the resulting field pattern then reduces to an integral over the path of an antenna conductor (modelled as a thin wire).
For the following derivation we shall take the current to be in the Z direction centered at the origin (x=y=z=0), with the sinusoidal time dependence 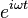 for all quantities being understood. The simplest approach is to use the calculation of the vector potential A(r) using the formula for the retarded potential. Although the value of A is not unique, we shall constrain it according to the Lorenz gauge, and assuming sinusoidal current at radian frequency ω the retardation of the field is converted just into a phase factor
for all quantities being understood. The simplest approach is to use the calculation of the vector potential A(r) using the formula for the retarded potential. Although the value of A is not unique, we shall constrain it according to the Lorenz gauge, and assuming sinusoidal current at radian frequency ω the retardation of the field is converted just into a phase factor 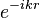 , where the wavenumber k = ω/c in free space and r is the distance between the point being considered to the origin (where we assumed the current to be), thus r = |r|. This results[15] in a vector potential A at position r due to that current element only, which we find is purely in the Z direction (the direction of the current):
, where the wavenumber k = ω/c in free space and r is the distance between the point being considered to the origin (where we assumed the current to be), thus r = |r|. This results[15] in a vector potential A at position r due to that current element only, which we find is purely in the Z direction (the direction of the current):
where μ0 is the permeability of free space. Then using
we can solve for the magnetic field H, and from that (dependent on us having chosen the Lorenz gauge) the electric field E using
 .
.
In spherical coordinates we find[16] that the magnetic field H has only a component in the φ direction:
while the electric field has components both in the θ and r directions:
where Z0 = √μ0 /ε0 is the impedance of free space.

This solution includes near field terms which are very strong near the source but which are not radiated. As seen in the accompanying animation, the E and H fields very close to the source are almost 90° out of phase, thus contributing very little to the Poynting vector by which radiated flux is computed. The near field solution for an antenna element (from the integral using this formula over the length of that element) is the field that can be used to compute the mutual impedance between it and another nearby element.
For computation of the far field radiation pattern, the above equations are simplified as only the 1/r terms remain significant:[16]
 .
.

The far field pattern is thus seen to consist of a transverse electromagnetic (TEM) wave, with electric and magnetic fields at right angles to each other and at right angles to the direction of propagation (the direction of r, as we assumed the source to be at the origin). The electric polarization, in the θ direction, is coplanar with the source current (in the Z direction), while the magnetic field is at right angles to that, in the φ direction. It can be seen from these equations, and also in the animation, that the fields at these distances are exactly in phase. Both fields fall according to 1/r, with the power thus falling according to 1/r2 as dictated by the inverse square law.
Radiation resistance
If one knows the far field radiation pattern due to a given antenna current, then it is possible to compute the radiation resistance directly. For the above fields due to the Hertzian dipole, we can compute the power flux according to the Poynting vector, resulting in a power (as averaged over one cycle) of:
Although not required, it is simplest to do the following exercise at a large r where the far field expressions for E and H apply. Consider a large sphere surrounding the source with a radius r. We find the power per unit area crossing the surface of that sphere to be in the  direction according to :
direction according to :
Integration of this flux over the complete sphere results in:
where  is the free space wavelength corresponding to the radian frequency ω. By definition, the radiation resistance Rrad times the average of the square of the current |I|2/2 is the net power radiated due to that current, so equating the above to |I|2Rrad/2 we find:
is the free space wavelength corresponding to the radian frequency ω. By definition, the radiation resistance Rrad times the average of the square of the current |I|2/2 is the net power radiated due to that current, so equating the above to |I|2Rrad/2 we find:
This method can be used to compute the radiation resistance for any antenna whose far field radiation pattern has been found in terms of a specific antenna current. If ohmic losses in the conductors are neglected, the radiation resistance (considered relative to the feedpoint) is identical to the resistive (real) component of the feedpoint impedance. Unfortunately this exercise tells us nothing about the reactive (imaginary) component of feedpoint impedance, whose calculation is considered below.
Directive gain
Using the above expression for the radiated flux given by the Poynting vector, it is also possible to compute the directive gain of the Hertzian dipole. Dividing the total power computed above by 4πr2 we can find the flux averaged over all directions Pavg as
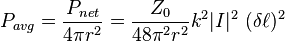 .
.
Dividing the flux radiated in a particular direction by Pavg we obtain the directive gain G(θ):
 .
.
The commonly quoted antenna "gain", meaning the peak value of the gain pattern (radiation pattern), is found to be 1.5 or 1.76 dBi, lower than practically any other antenna configuration.
Comparison with the short dipole
The Hertzian dipole is similar to but differs from the short dipole, discussed above. In both cases the conductor is very short compared to a wavelength, so the standing wave pattern present on a half wave dipole (for instance) is absent. However, with the Hertzian dipole we specified that the current along that conductor is constant over its short length. This is makes the Hertzian dipole useful for analysis of more complex antenna configurations, where every infinitesimal section of that real antenna's conductor can be modelled as a Hertzian dipole with the current found to be flowing in that real antenna.
However a short conductor fed with a RF voltage will not have a uniform current even along that short range. Rather, a short dipole in real life has a current equal to the feedpoint current at the feedpoint but falling linearly to zero over the length of that short conductor. By placing a capacitive hat, such as a metallic ball, at the end of the conductor, it is possible for its self capacitance to absorb the current from the conductor and better approximate the constant current assumed for the Hertzian dipole. But again, the Hertzian dipole is meant only as a theoretical construct for antenna analysis.
The short dipole, with a feedpoint current of I0, has an average current over each conductor of only I0/2. The above field equations for the Hertzian dipole of length δℓ would then predict the actual fields for a short dipole using that effective current I = I0/2. This would result in a power measured in the far field of one quarter that given by the above equation for the Poynting vector  if we had assumed an element current of I0. Consequently, it can be seen that the radiation resistance computed for the short dipole is one quarter of that computed above for the Hertzian dipole. But their radiation patterns (and gains) are identical.
if we had assumed an element current of I0. Consequently, it can be seen that the radiation resistance computed for the short dipole is one quarter of that computed above for the Hertzian dipole. But their radiation patterns (and gains) are identical.
Detailed calculation of dipole feedpoint impedance
The impedance seen at the feedpoint of a dipole of various lengths has been plotted above, in terms of the real (resistive) component Rdipole and the imaginary (reactive) component jXdipole of that impedance. For the case of an antenna with perfect conductors (no ohmic loss), Rdipole is identical to the radiation resistance, which can more easily be computed from the total power in the far-field radiation pattern for a given applied current as we showed for the short dipole. The calculation of Xdipole is more difficult.
Induced EMF method
Using the induced EMF method closed form expressions are obtained for both components of the feedpoint impedance; such results are plotted above. The solution depends on an assumption for the form of the current distribution along the antenna conductors. For wavelength to element diameter ratios greater than about 60, the current distribution along each antenna element is very well approximated [15] as a sine wave along each conductor:
where L is the full length of the dipole, z is the position along the dipole relative to the feedpoint, k is the wavenumber equal to 2π/λ (λ being the wavelength, λ=c/f for an antenna in free space), and A is an amplitude chosen to match an assumed driving point current by setting z=0.
In cases where an approximately sinusoidal current distribution can be assumed, this method solves for the driving point impedance in closed form using the cosine and sine integral functions Si(x) and Ci(x). For a dipole of total length L using conductors with a radius a operating at a frequency with wavenumber k (k = 2πf/c in free space) in a medium with characteristic impedance Zm (usually Z0 with the antenna in free space), then the resistance R and reactance X of the driving point impedance can be expressed as:
where γ is the Euler constant.[17]
This computation using the induced EMF method is identical to the computation of the mutual impedance between two dipoles (with infinitesimal conductor radius) separated by the distance a. Because the field at or beyond the edge of an antenna's cylindrical conductor at a distance a is only dependent on the current distribution along the conductor, and not the radius of the conductor, that field is used to compute the mutual impedance between that filamentary antenna and the actual position of the conductor with a radius a. This then supplies the self-impedance of the conductor itself.
Integral methods
Note that the induced EMF method is dependent on the assumption of a sinusoidal current distribution, delivering an accuracy better than about 10% as long as the wavelength to element diameter ratio is greater than about 60.[15] However, for yet larger conductors numerical solutions are required which solve for the conductor's current distribution (rather than assuming a sinusoidal pattern). This can be based on approximating solutions for either Pocklington's integrodifferential equation or the Hallén integral equation.[6] These approaches also have greater generality, not being limited to linear conductors.
Numerical solution of either is performed using the moment method solution which requires expansion of that current into a set of basis functions; one simple (but not the best) choice, for instance, is to break up the conductor into N segments with a constant current assumed along each. After setting an appropriate weighting function the cost may be minimized through the inversion of a NxN matrix. Determination of each matrix element requires at least one double integration involving the weighting functions, which may become computationally intensive. These are simplified if the weighting functions are simply delta functions, which corresponds to fitting the boundary conditions for the current along the conductor at only N discrete points. Then the NxN matrix must be inverted, which is also computationally intensive as N increases. In one simple example,[6] Balanis performs this computation to find the antenna impedance with different N using Pocklington's method and finds that with N>60 solutions have approached their limiting values to within a few percent.
Feeding a dipole using a balun


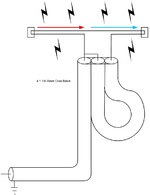

A dipole is a symmetrical antenna, as it is composed of two symmetrical ungrounded elements. Therefore, it works best when fed by a balanced transmission line, such as a ladder line, because in that case the symmetry (one aspect of the impedance complex, which is a complex number) matches and therefore the power transfer is extremal.
When a dipole with an unbalanced feedline such as coaxial cable is used for transmitting, the shield side of the cable, in addition to the antenna, radiates.[11] This can induce radio frequency (RF) currents into other electronic equipment near the radiating feedline, causing RF interference. Furthermore, the antenna is not as efficient as it could be because it is radiating closer to the ground and its radiation pattern may be asymmetrically distorted. At higher frequencies, where the length of the dipole becomes significantly shorter than the diameter of the feeder cable, this becomes a more significant problem. To prevent this, dipoles fed by coaxial cables have a balun between the cable and the antenna, to convert the unbalanced signal provided by the coax to a balanced symmetrical signal for the antenna.
Several types of balun are commonly used to feed a dipole antenna: current baluns and coax baluns. Baluns can be made using ferrite toroid cores or even from the coax feedline itself.[18] The choice of the toroid core is crucial. A rule of thumb is: the more power, the bigger the core.[19]
Current balun
A current balun consists of two windings that are closely coupled.[11][20]
Coax balun
A coax balun is a cost-effective method of eliminating feeder radiation, but is limited to a narrow set of operating frequencies.
One easy way to make a balun is to use a length of coaxial cable equal to half a wavelength. The inner core of the cable is linked at each end to one of the balanced connections for a feeder or dipole. One of these terminals should be connected to the inner core of the coaxial feeder. All three braids should be connected together. This then forms a 4:1 balun, which works correctly at only a narrow band of frequencies.
Sleeve balun
At VHF frequencies, a sleeve balun can also be built to remove feeder radiation.[21]
Another narrow-band design is to use a λ/4 length of metal pipe. The coaxial cable is placed inside the pipe; at one end the braid is wired to the pipe while at the other end no connection is made to the pipe. The balanced end of this balun is at the end where the pipe is wired to the braid. The λ/4 conductor acts as a transformer, converting the infinite impedance at the unconnected end into a zero impedance at the end connected to the braid. Hence any current entering the balun through the connection, which goes to the braid at the end with the connection to the pipe, will flow into the pipe. This balun design is impractical for low frequencies because of the long length of pipe that will be needed.
Dipole as a reference standard
Antenna gain is sometimes measured as decibels relative to a half-wave dipole, which means that the antenna in question is being compared to a dipole, and has a certain amount of gain relative to a dipole antenna tuned to the same operating frequency. In this case, one says the antenna has a gain of "x dBd" (see decibel). More often, gains are expressed relative to an isotropic radiator, which is an imaginary antenna that radiates equally in all directions. In this case one uses dBi instead of dBd (see decibel). As it is impossible to build an isotropic radiator, gain measurements expressed relative to a dipole are more practical when a reference dipole aerial is used for experimental measurements. 0 dBd is often considered equal to 2.15 dBi.
See also
- Electronic symbol
- Isotropic antenna
- Omnidirectional antenna
- Whip antenna
- Driven element
- Balun
- Coaxial antenna
- Amateur radio
- Shortwave listening
- T-aerial
- AM broadcasting
- FM broadcasting
- Dipole field strength in free space
References
- 1 2 Winder, Steve; Joseph Carr (2002). Newnes Radio and RF Engineering Pocket Book, 3rd Ed. Newnes. p. 4. ISBN 0080497470.
- ↑ Der Dipol in Theorie und Praxis, K. Hille (DL1VU)
- 1 2 3 4 Basu, Dipak (2010). Dictionary of Pure and Applied Physics, 2nd Ed. CRC Press. p. 21. ISBN 1420050222.
- 1 2 "Dipole Antenna / Aerial tutorial". Resources. Radio-Electronics.com, Adrio Communications, Ltd. 2011. Retrieved April 29, 2013.
- ↑ Rouse, Margaret (2003). "Dipole Antenna". Online IT Encyclopedia. TechTarget.com. Retrieved April 29, 2013. External link in
|publisher=(help) - 1 2 3 4 Balanis, Constantine A. (2011). Modern Antenna Handbook. John Wiley & Sons. p. 2.3. ISBN 1118209753.
- ↑ Stutzman, Warren L.; Thiele, Gary A. (2012). Antenna Theory and Design. John Wiley and Sons. pp. 74–75. ISBN 0470576642.
- ↑ Below 30 MHz, atmospheric noise is high; consequently, received power levels must be significantly above the thermal noise floor. The receiving antenna's inefficiency is masked by the higher power level. See Rohde, Communications Receivers, discussion on active antennas.
- ↑ Amlaner, Charles J. Jr. (March 1979). "The design of antennas for use in radio telemetry". A Handbook on Biotelemetry and Radio Tracking: Proceedings of an International Conference on Telemetry and Radio Tracking in Biology and Medicine, Oxford, 20–22 March 1979. Elsevier. p. 254. Retrieved December 5, 2014.
- ↑ ycars.org - Reflections and standing wave ratio, 2011-01-30
- 1 2 3 Baluns: What They Do And How They Do It (W7EL) http://www.eznec.com/Amateur/Articles/Baluns.pdf
- ↑ Practical Wire Antennas 2 (I. Poole, G3YWX)
- 1 2 3 Silver, Samuel (1984). Microwave Antenna Theory and Design. pp. 98–99.
- ↑ Mushiake, Yasuto (October 1954). "An Exact Impedance Step-Up Impedance-Ratio Chart of a Folded Antenna". IRE. Trans. Ant. Prop. AP–3 (4): 163. Retrieved 2014-01-10.
- 1 2 3 Lee, Kai Fong (1984). Principles of Antenna Theory. John Wiley & Sons Ltd. pp. 29, 42. ISBN 0 471 90167 9.
- 1 2 Silver, Samuel (1949). Microwave Antenna Theory and Design. pp. 92–94.
- ↑ Chaotic behavior in receiver front-end limiters, F Caudron & A Ouslimani, Progress in Electromagnetics Research Letters, Vol 23 19-28 2011, pp 23-24
- ↑ Baluns for 88–108 MHz B. Beezely (K6STI) http://www.ham-radio.com/k6sti/balun.htm
- ↑ Toroid Cores for 1:4 Baluns (DG3OBK) http://www.aroesner.homepage.t-online.de/balun.html
- ↑ A Cost Effective Current-mode 1:1 Balun (R. Holland) http://www.arising.com.au/people/Holland/Ralph/CMBalun.htm
- ↑ Sleeve Baluns
Elementary, short and half-wave dipoles:
- Terman, Federick R.; Helliwell, Robert (1955), Electronic Radio and Engineering (4th ed.), MacGraw-Hill, ISBN 978-0-07-085795-7
- Feynman; Leighton; Sands, Lectures on Physics, Addison-Wesley
- Panofsky, W.; Phillips, M., Classical Electricity and Magnetism, Addison-Wesley
- http://www.ece.rutgers.edu/~orfanidi/ewa/ Electromagnetic Waves and Antennas, Sophocles J. Orfanidis.
- Wire Antenna Resources for Ham Radio Wire Antenna Resources including off center fed dipole (OCFD), dipole calculators and construction sites
- http://stewks.ece.stevens-tech.edu/sktpersonal.dir/sktwireless/lin-ant.pdf
- http://www.nt.hs-bremen.de/peik/asc/asc_antenna_slides.pdf
- The Hertzian dipole
- The ARRL Antenna Book (21st ed.), The American Radio Relay League, Inc., 2007, ISBN 0-87259-987-6
- ARRL's Wire Antenna Classics - A collection of the best articles from ARRL publications 1 (First ed.), The American Radio Relay League, Inc., 2005, ISBN 0-87259-707-5
- Reflections on Hertz and the Hertzian Dipole Jed Z. Buchwald, MIT and the Dibner Institute for the History of Science and Technology (link inactive February 2, 2007; archive accessed from Wayback, March 13, 2011)
External links
- Dipole Antenna Tutorial EM Talk
- Broadband Dipoles Antenna-Theory.com
- AC6V's Homebrew Antennas Links
- Your First HF Dipole - simple yet complete tutorial from eham.net
| ||||||||||||||||||||||||||||||||||||||||||







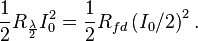




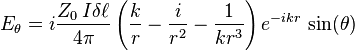

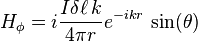

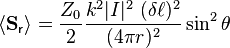



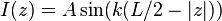
![\begin{align}
R_\mathrm{dipole} &= \frac{Z_m}{2 \pi \sin^2(kL/2)} \Big\{
\gamma + \ln(kL) - \operatorname{Ci}(kL) + \tfrac{1}{2}\sin(kL) \big[\operatorname{Si}(2kL)- 2\operatorname{Si}(kL)\big] \\
&\qquad\qquad\qquad\qquad + \tfrac{1}{2}\cos(kL)\big[ \gamma + \ln(kL/2) + \operatorname{Ci}(2kL) - 2\operatorname{Ci}(kL) \big]
\Big\}
\end{align}](../I/m/6a269f83aad62922397181ba268edf91.png)
![\begin{align}
X_\mathrm{dipole} &= \frac{Z_m}{ 4 \pi \sin^2(kL/2)} \Big\{
2 \operatorname{Si}(kL) + \cos(kL)\big[ 2 \operatorname{Si}(kL) - \operatorname{Si}(2kL) \big] \\
&\qquad\qquad\qquad\qquad - \sin(kL)\big[ 2 \operatorname{Ci}(kL) - \operatorname{Ci}(2kL) - \operatorname{Ci}(2ka^2/L) \big]
\Big\},
\end{align}](../I/m/97cb91e62e95b94f7a48de4983c5c392.png)