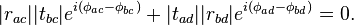Beam splitter

Schematic illustration of a beam splitter cube.
1 - Incident light
2 - 50% Transmitted light
3 - 50% Reflected light
In practice, the reflective layer absorbs some light.

Beam splitters

Beam splitter designs

In its most common form, a cube, it is made from two triangular glass prisms which are glued together at their base using polyester, epoxy, or urethane-based adhesives. The thickness of the resin layer is adjusted such that (for a certain wavelength) half of the light incident through one "port" (i.e., face of the cube) is reflected and the other half is transmitted due to frustrated total internal reflection. Polarizing beam splitters, such as the Wollaston prism, use birefringent materials, splitting light into beams of differing polarization.

Aluminum coated beam splitter.

Another design is the use of a half-silvered mirror, a sheet of glass or plastic with a transparently thin coating of metal, now usually aluminium deposited from aluminium vapor. The thickness of the deposit is controlled so that part (typically half) of the light which is incident at a 45-degree angle and not absorbed by the coating is transmitted, and the remainder is reflected. A very thin half-silvered mirror used in photography is often called a pellicle mirror. To reduce loss of light due to absorption by the reflective coating, so-called "swiss cheese" beam splitter mirrors have been used. Originally, these were sheets of highly polished metal perforated with holes to obtain the desired ratio of reflection to transmission. Later, metal was sputtered onto glass so as to form a discontinuous coating, or small areas of a continuous coating were removed by chemical or mechanical action to produce a very literally "half-silvered" surface.

Instead of a metallic coating, a dichroic optical coating may be used. Depending on its characteristics, the ratio of reflection to transmission will vary as a function of the wavelength of the incident light. Dichroic mirrors are used in some ellipsoidal reflector spotlights to split off unwanted infrared (heat) radiation, and as output couplers in laser construction.

A third version of the beam splitter is a dichroic mirrored prism assembly which uses dichroic optical coatings to divide an incoming light beam into a number of spectrally distinct output beams. Such a device was used in three-pickup-tube color television cameras and the three-strip Technicolor movie camera. It is currently used in modern three-CCD cameras. An optically similar system is used in reverse as a beam-combiner in three-LCD projectors, in which light from three separate monochrome LCD displays is combined into a single full-color image for projection.

Beam splitters with single mode fiber for PON networks use the single mode behavior to split the beam. The splitter is done by physically splicing two fibers "together" as an X.

Arrangements of mirrors or prisms used as camera attachments to photograph stereoscopic image pairs with one lens and one exposure are sometimes called "beam splitters", but that is a misnomer, as they are effectively a pair of periscopes redirecting rays of light which are already non-coincident. In some very uncommon attachments for stereoscopic photography, mirrors or prism blocks similar to beam splitters perform the opposite function, superimposing views of the subject from two different perspectives through color filters to allow the direct production of an anaglyph 3D image, or through rapidly alternating shutters to record sequential field 3D video.

Phase shift

Phase shift through a beam splitter with a dielectric coating.

A beam splitter that consists of a glass plate with a reflective dielectric coating on one side gives a phase shift of 0 or π, depending on the side from which it is incident (see figure).^[1] Transmitted waves have no phase shift. Reflected waves entering from the reflective side (red) are phase-shifted by π, whereas reflected waves entering from the glass side (blue) have no phase shift. This is due to the Fresnel equations, according to which reflection causes a phase shift only when light passing through a material of low refractive index is reflected at a material of high refractive index. This is the case in the transition of air to reflector, but not from glass to reflector (given that the refractive index of the reflector is in between that of glass and that of air).

This does not apply to partial reflection by conductive (metallic) coatings, where other phase shifts occur in all paths (reflected and transmitted).

Classical lossless beam splitter

We consider a classical lossless beam-splitter with electric fields incident at both its inputs. The two output fields E_c and E_d are linearly related to the inputs through

\begin{bmatrix} E_c \\ E_d \end{bmatrix} = \begin{bmatrix} r_{ac}& t_{bc} \\ t_{ad}& r_{bd} \end{bmatrix} \begin{bmatrix} E_a \\ E_b \end{bmatrix},

where the 2 × 2 element is the beam-splitter matrix. r and t are the reflectance and transmittance along a particular path through the beam-splitter, that path being indicated by the subscripts.

Assuming the beam-splitter removes no energy from the light beams, the total output energy can be equated with the total input energy, reading

|E_c|^2+|E_d|^2=|E_a|^2+|E_b|^2.

Requiring this energy conservation brings about the relationships between reflectance and transmittance

|r_{ac}|^2+|t_{ad}|^2=|r_{bd}|^2+|t_{bc}|^2=1

and

r_{ac}t^{\ast}_{bc}+t_{ad}r^{\ast}_{bd}=0,

where " $^\ast$ " indicates the complex conjugate. Expanding, we can write each r and t as a complex number having an amplitude and phase factor; for instance, $r_{ac}=|r_{ac}|e^{i\phi_{ac}}$ . The phase factor accounts for possible shifts in phase of a beam as it reflects or transmits at that surface. We then obtain

|r_{ac}||t_{bc}|e^{i(\phi_{ac}-\phi_{bc})}+|t_{ad}||r_{bd}|e^{i(\phi_{ad}-\phi_{bd})}=0.

Further simplifying we obtain the relationship

\frac{|r_{ac}|}{|t_{ad}|}=-\frac{|r_{bd}|}{|t_{bc}|}e^{i(\phi_{ad}-\phi_{bd}+\phi_{bc}-\phi_{ac})}

which is true when 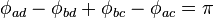$\phi_{ad}-\phi_{bd}+\phi_{bc}-\phi_{ac}=\pi$ and the exponential term reduces to -1. Applying this new condition and squaring both sides, we obtain

\frac{1-|t_{ad}|^2}{|t_{ad}|^2}=\frac{1-|t_{bc}|^2}{|t_{bc}|^2},

where substitutions of the form $|r_{ac}|^2=1-|t_{ad}|^2$ were made. This leads us to the result

|t_{ad}|=|t_{bc}|\equiv T,

and similarly,

|r_{ac}|=|r_{bd}|\equiv R.

It follows that 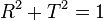$R^2+T^2=1$ .

Now that the constraints describing a lossless beam-splitter have been determined, we can rewrite our initial expression as

\begin{bmatrix} E_c \\ E_d \end{bmatrix} = \begin{bmatrix} Re^{i\phi_{ac}}& Te^{i\phi_{bc}} \\ Te^{i\phi_{ad}}& Re^{i\phi_{bd}} \end{bmatrix} \begin{bmatrix} E_a \\ E_b \end{bmatrix}.

^[2]

Use in experiments

Several experiments in quantum theory and relativity theory and other fields of physics use beam splitters (usually in interferometers); these include:

The Fizeau experiment of 1851 to measure the speeds of light in water
The Michelson-Morley experiment of 1887 to measure the effect of the (hypothetical) luminiferous aether on the speed of light
- The Hammar experiment of 1935 to refute Dayton Miller's claim of a positive result from repetitions of the Michelson-Morley experiment
The Kennedy-Thorndike experiment of 1932 to test the independence of the speed of light and the velocity of the measuring apparatus
Bell test experiments (from ca. 1972) to demonstrate consequences of quantum entanglement and exclude local hidden variable theories
Wheeler's delayed choice experiment of 1978, 1984 etc., a series of thought experiments in quantum mechanics to test what makes a photon behave as a wave or a particle and when it happens
The FELIX experiment (proposed in 2000) to test the Penrose interpretation that quantum superposition depends on space-time curvature
The many uses of the Mach–Zehnder interferometer in areas such as quantum mechanics and quantum computation

Quantum mechanical description

We consider two single mode input fields, denoted by the annihilation operators $\hat{a}_{0},\hat{a}_{1}$ which incident on the two input ports of the beam splitter. The two output fields, denoted by $\hat{a}_{2},\hat{a}_{3},$ are linearly related to the input field by ^[3]

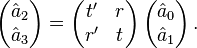
$\left(\begin{matrix} \hat{a}_{2}\\ \hat{a}_{3} \end{matrix}\right)=\left(\begin{matrix} t' & r\\ r' & t \end{matrix}\right)\left(\begin{matrix} \hat{a}_{0}\\ \hat{a}_{1} \end{matrix}\right).$

In order to obtain the entries of the transformation matrix one must take into account that the commutation relations of the fields hold. As is well-known from second quantization, one must make sure that

$[\hat{a}_{i},\hat{a}_{j}^{\dagger}]=\delta_{ij}$

and

$[\hat{a}_{i},\hat{a}_{j}]=0.$

This, together with energy conservation yields the following set of constraints:

$|r'|=|r|,\,|t'|=|t|,\,|r|^{2}+|t|^{2}=1$

$r^{*}t'+r't^{*}=r^{*}t+r't'^{*}=0.$

For a dielectric 50:50 beam splitter the reflected and transmitted beams differ in phase by 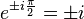$e^{\pm i\frac{\pi}{2}}=\pm i$ . Assuming the reflected beam suffers a 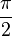$\frac{\pi}{2}$ phase shift, the input and output fields are related by:

$\hat{a}_{2}=\frac{1}{\sqrt{2}}\left(\hat{a}_{0}+i\hat{a}_{1}\right)\,\hat{a}_{3}=\frac{1}{\sqrt{2}}\left(i\hat{a}_{0}+\hat{a}_{1}\right).$

The unitary transformation associated with this transformation is

$\hat{U}=e^{i\frac{\pi}{4}\left(\hat{a}_{0}^{\dagger}\hat{a}_{1}+\hat{a}_{0}\hat{a}_{1}^{\dagger}\right)}.$

Using this unitary, one can also write the transforms as

$\left(\begin{matrix} \hat{a}_{2}\\ \hat{a}_{3} \end{matrix}\right)=\hat{U}^{\dagger}\left(\begin{matrix} \hat{a}_{0}\\ \hat{a}_{1} \end{matrix}\right)\hat{U}$

Application for quantum computing

In 2000 Knill, Laflamme and Milburn (KLM protocol) proved that it is possible to create universal quantum computer solely with beam splitters, phase shifters, photodetectors and single photon sources. The states that form a qubit in this protocol are the one photon states of two modes, i.e. the states |01> and |10> in the occupation number representation (Fock state) of two modes. Using these resources it's possible to implement any single qubit gate and 2-qubit probabilistic gates. The beam splitter is an essential component in this scheme since it's the only one that creates entanglement between the Fock states.

References

Wikimedia Commons has media related to Beam splitters.

↑ Zetie, K P; Adams, S F; Tocknell, R M, How does a Mach–Zehnder interferometer work? (PDF), retrieved 13 February 2014
↑ R. Loudon, The quantum theory of light, third edition, Oxford University Press, New York, NY, 2000.
↑ Knight, Christopher Gerry, Peter (2005). Introductory quantum optics (3. print. ed.). New York: Cambridge University Press. ISBN 052152735X.

This article is issued from Wikipedia - version of the Tuesday, December 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.