Half-exponential function
In mathematics, a half-exponential function is a function ƒ so that if ƒ is composed with itself the result is exponential:[1]
Another definition is that ƒ is half-exponential if it is non-decreasing and ƒ−1(xC) ≤ o(log x). for every C > 0.[2]
It has been proven that every function ƒ composed of basic arithmetic operations, exponentials, and logarithms, then ƒ(ƒ(x)) is either subexponential or superexponential:[3] half-exponential functions are not expressible in terms of elementary functions.
There are infinitely many functions whose self-composition is the same exponential function as each other. In particular, for every  in the open interval
in the open interval  and for every continuous strictly increasing function g from
and for every continuous strictly increasing function g from ![[0,A]](../I/m/0c9ad80871fb8909dbd6499da2f961c2.png) onto
onto ![[A,1]](../I/m/8bec40d316aa77a3f11cdbd28b46782c.png) , there is an extension of this function to a continuous monotonic function
, there is an extension of this function to a continuous monotonic function  on the real numbers such that
on the real numbers such that 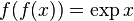 .[4] In particular,
.[4] In particular,
Half-exponential functions are used in computational complexity theory for growth rates "intermediate" between polynomial and exponential.[1]
See also
References
- 1 2 Peter Bro Miltersen, N. V. Vinodchandran, Osamu Watanabe (1999). "Super-Polynomial Versus Half-Exponential Circuit Size in the Exponential Hierarchy". Lecture Notes in Computer Science 1627: 210–220. doi:10.1007/3-540-48686-0_21.
- ↑ Alexander A. Razborov and Steven Rudich (August 1997). "Natural Proofs". Journal of Computer and System Sciences 55 (1): 24–35. doi:10.1006/jcss.1997.1494.
- ↑ "Shtetl-Optimized » Blog Archive » My Favorite Growth Rates". Scottaaronson.com. 2007-08-12. Retrieved 2014-05-20.
- ↑ Crone, Lawrence J.; Neuendorffer, Arthur C. (1988). "Functional powers near a fixed point". Journal of Mathematical Analysis and Applications 132 (2): 520–529. doi:10.1016/0022-247X(88)90080-7. MR 943525.
External links
- http://mathoverflow.net/questions/12081/does-the-exponential-function-have-a-square-root
- http://mathoverflow.net/questions/45477/closed-form-functions-with-half-exponential-growth
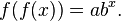
![f (x) =
\begin{cases}
g (x) & \mbox{if } x \in [0,A], \\
\exp (g^{-1} (x)) & \mbox{if } x \in (A,1], \\
\exp (f ( \ln (x))) & \mbox{if } x \in (1,\infty), \\
\ln (f ( \exp (x))) & \mbox{if } x \in (-\infty,0). \\
\end{cases}](../I/m/44a9884c65205a7c2308cf505b4ea026.png)