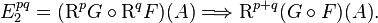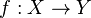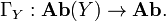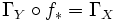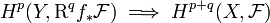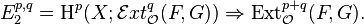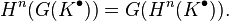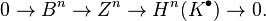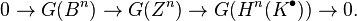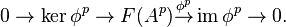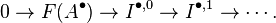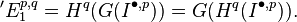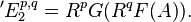Grothendieck spectral sequence

In mathematics, in the field of homological algebra, the Grothendieck spectral sequence, introduced in Tôhoku paper, is a spectral sequence that computes the derived functors of the composition of two functors 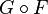$G\circ F$ , from knowledge of the derived functors of F and G.

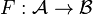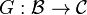If $F :\mathcal{A}\to\mathcal{B}$ and $G :\mathcal{B}\to\mathcal{C}$ are two additive and left exact functors between abelian categories such that $F$ takes F-acyclic objects (e.g., injective objects) to $G$ -acyclic objects and if $\mathcal{B}$ has enough injectives, then there is a spectral sequence for each object $A$ of $\mathcal{A}$ that admits an F-acyclic resolution:

E_2^{pq} = ({\rm R}^p G \circ{\rm R}^q F)(A) \Longrightarrow {\rm R}^{p+q} (G\circ F)(A).

Many spectral sequences in algebraic geometry are instances of the Grothendieck spectral sequence, for example the Leray spectral sequence.

The exact sequence of low degrees reads

0 → R¹G(FA) → R¹(GF)(A) → G(R¹F(A)) → R²G(FA) → R²(GF)(A).

Examples

The Leray spectral sequence

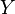If $X$ and $Y$ are topological spaces, let

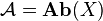\mathcal{A} = \mathbf{Ab}(X)

and

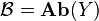\mathcal{B} = \mathbf{Ab}(Y)

be the category of sheaves of abelian groups on X and Y, respectively and

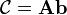\mathcal{C} = \mathbf{Ab}

be the category of abelian groups.

For a continuous map

f : X \to Y

there is the (left-exact) direct image functor

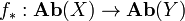f_* : \mathbf{Ab}(X) \to \mathbf{Ab}(Y)

We also have the global section functors

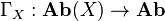\Gamma_X : \mathbf{Ab}(X)\to \mathbf{Ab}

and

\Gamma_Y : \mathbf{Ab}(Y) \to \mathbf {Ab}.

Then since

\Gamma_Y \circ f_* = \Gamma_X

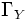and the functors $f_*$ and $\Gamma_Y$ satisfy the hypotheses (since the direct image functor has an exact left adjoint 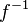$f^{-1}$ , pushforwards of injectives are injective and in particular acyclic for the global section functor), the sequence in this case becomes:

H^p(Y,{\rm R}^q f_*\mathcal{F})\implies H^{p+q}(X,\mathcal{F})

for a sheaf $\mathcal{F}$ of abelian groups on $X$ , and this is exactly the Leray spectral sequence.

Local-to-global Ext spectral sequence

There is a spectral sequence relating the global Ext and the sheaf Ext: let F, G be sheaves of modules over a ringed space $(X, \mathcal{O})$ ; e.g., a scheme. Then

E^{p,q}_2 = \operatorname{H}^p(X; \mathcal{E}xt^q_{\mathcal{O}}(F, G)) \Rightarrow \operatorname{Ext}^{p+q}_{\mathcal{O}}(F, G).

^[1]

This is an instance of the Grothendieck spectral sequence: indeed,

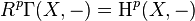R^p \Gamma(X, -) = \operatorname{H}^p(X, -)

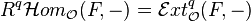R^q \mathcal{H}om_{\mathcal{O}}(F, -) = \mathcal{E}xt^q_{\mathcal{O}}(F, -)

and

R^n \Gamma(X, \mathcal{H}om_{\mathcal{O}}(F, -)) = \operatorname{Ext}^n_{\mathcal{O}}(F, -)

Moreover, 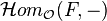$\mathcal{H}om_{\mathcal{O}}(F, -)$ sends injective $\mathcal{O}$ -modules to flaque sheaves,^[2] which are $\Gamma(X, -)$ -acyclic. Hence, the hypothesis is satisfied.

Derivation

We shall use the following lemma:

Lemma — If K is an injective complex in an abelian category C such that the kernels of the differentials are injective objects, then for each n,

H^n(K^{\bullet})

is an injective object and for any left-exact additive functor G on C,

H^n(G(K^{\bullet})) = G(H^n(K^{\bullet})).

Proof: Let 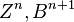$Z^n, B^{n+1}$ be the kernel and the image of 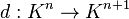$d: K^n \to K^{n+1}$ . We have

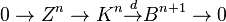0 \to Z^n \to K^n \overset{d}\to B^{n+1} \to 0

which splits and implies 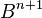$B^{n+1}$ is injective and the first part of the lemma. Next we look at

0 \to B^n \to Z^n \to H^n(K^{\bullet}) \to 0.

It splits. Thus,

0 \to G(B^n) \to G(Z^n) \to G(H^n(K^{\bullet})) \to 0.

Similarly we have (using the early splitting):

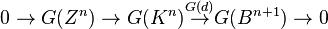0 \to G(Z^n) \to G(K^n) \overset{G(d)} \to G(B^{n+1}) \to 0

The second part now follows. $\square$

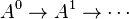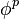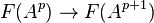We now construct a spectral sequence. Let $A^0 \to A^1 \to \cdots$ be an F-acyclic resolution of A. Writing $\phi^p$ for $F(A^p) \to F(A^{p+1})$ , we have:

0 \to \operatorname{ker} \phi^p \to F(A^p) \overset{\phi^p}\to \operatorname{im} \phi^p \to 0.

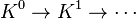Take injective resolutions $J^0 \to J^1 \to \cdots$ and $K^0 \to K^1 \to \cdots$ of the first and the third nonzero terms. By the horseshoe lemma, their direct sum 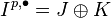$I^{p, \bullet} = J \oplus K$ is an injective resolution of 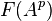$F(A^p)$ . Hence, we found an injective resolution of the complex:

0 \to F(A^{\bullet}) \to I^{\bullet, 0} \to I^{\bullet, 1} \to \cdots.

such that each row 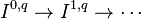$I^{0, q} \to I^{1, q} \to \cdots$ satisfies the hypothesis of the lemma (cf. the Cartan–Eilenberg resolution.)

Now, the double complex 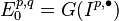$E_0^{p, q} = G(I^{p, \bullet})$ gives rise to two spectral sequences, horizontal and vertical, which we are now going to examine. On the one hand, by definition,

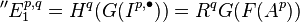{}^{\prime \prime} E_1^{p, q} = H^q(G(I^{p, \bullet})) = R^q G(F(A^p))

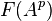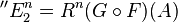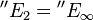which is always zero unless q = 0 since $F(A^p)$ is G-acyclic by hypothesis. Hence, ${}^{\prime \prime} E_{2}^n = R^n (G \circ F) (A)$ and ${}^{\prime \prime} E_2 = {}^{\prime \prime} E_{\infty}$ . On the other hand, by the definition and the lemma,

{}^{\prime} E^{p, q}_1 = H^q(G(I^{\bullet, p})) = G(H^q(I^{\bullet, p})).

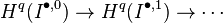Since $H^q(I^{\bullet, 0}) \to H^q(I^{\bullet, 1}) \to \cdots$ is an injective resolution of $H^q(F(A^{\bullet})) = R^q F(A)$ (it is a resolution since its cohomology is trivial),

{}^{\prime} E^{p, q}_2 = R^p G(R^qF(A)).

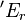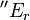Since ${}^{\prime} E_r$ and ${}^{\prime \prime} E_r$ have the same limiting term, the proof is complete. $\square$

Notes

↑ Godement, Ch. II, Theorem 7.3.3.
↑ Godement, Ch. II, Lemma 7.3.2.

References

Godement, Roger (1973), Topologie algébrique et théorie des faisceaux, Paris: Hermann, MR 0345092
Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR 1269324

This article incorporates material from Grothendieck spectral sequence on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia - version of the Wednesday, July 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.