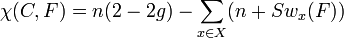Grothendieck–Ogg–Shafarevich formula
Not to be confused with Néron–Ogg–Shafarevich criterion.
In mathematics, the Grothendieck–Ogg–Shafarevich formula describes the Euler characteristic of complete curve with coefficients in an abelian variety or constructible sheaf, in terms of local data involving the Swan conductor. Ogg (1962) and Shafarevich (1961) proved the formula for abelian varieties with tame ramification over curves, and Grothendieck (1977, Exp. X formula 7.2) extended the formula to constructible sheaves over a curve (Raynaud 1965).
Statement
Suppose that F is a constructible sheaf over a genus g smooth projective curve C, of rank n outside a finite set X of points where it has stalk 0. Then
where Sw is the Swan conductor at a point.
References
- Grothendieck, Alexandre (1977), Séminaire de Géométrie Algébrique du Bois Marie – 1965–66 – Cohomologie l-adique et Fonctions L – (SGA 5), Lecture notes in mathematics (in French) 589, Berlin; New York: Springer-Verlag, xii+484, doi:10.1007/BFb0096802, ISBN 3540082484
- Ogg, A. P. (1962), "Cohomology of abelian varieties over function fields", Annals of Mathematics. Second Series 76: 185–212, ISSN 0003-486X, JSTOR 1970272, MR 0155824
- Raynaud, Michel (1965), "Caractéristique d'Euler–Poincaré d'un faisceau et cohomologie des variétés abéliennes", Séminaire Bourbaki, Vol. 9, Exp. No. 286, Paris: Société Mathématique de France, pp. 129–147, MR 1608794
- Shafarevich, Igor R. (1961), "Principal homogeneous spaces defined over a function field", Akademiya Nauk SSSR. Trudy Matematicheskogo Instituta imeni V. A. Steklova 64: 316–346, ISSN 0371-9685, MR 0162806
This article is issued from Wikipedia - version of the Saturday, November 08, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.