Graph realization problem
The graph realization problem is a decision problem in graph theory. Given a finite sequence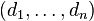 
of natural numbers, the problem asks whether there is labeled simple graph such that 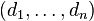is the degree sequence of this graph.
Solutions
The problem can be solved in polynomial time. One method of showing this uses the Havel–Hakimi algorithm constructing a special solution with the use of a recursive algorithm.[1][2] Alternatively, following the characterization given by the Erdős–Gallai theorem, the problem can be solved by testing the validity of 
inequalities.[3]
Other notations
The problem can also be stated in terms of symmetric matrices of zeros and ones. The connection can be seen if one realizes that each graph has an adjacency matrix where the column sums and row sums correspond to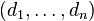 
. The problem is then sometimes denoted by symmetric 0-1-matrices for given row sums.
Related problems
Similar problems describe the degree sequences of simple bipartite graphs or the degree sequences of simple directed graphs. The first problem is the so-called bipartite realization problem. The second is known as the digraph realization problem.
The problem of constructing a solution for the graph realization problem with the additional constraint that each such solution comes with the same probability was shown to have a polynomial-time approximation scheme for the degree sequences of regular graphs by Cooper et al.[4] The general problem is still unsolved.
References
- ↑ Havel, Václav (1955), "A remark on the existence of finite graphs", Časopis pro pěstování matematiky (in Czech) 80: 477–480.
- ↑ Hakimi, S. L. (1962), "On realizability of a set of integers as degrees of the vertices of a linear graph. I", Journal of the Society for Industrial and Applied Mathematics 10: 496–506, MR 0148049.
- ↑ Erdős, P.; Gallai, T. (1960), "Gráfok előírt fokszámú pontokkal" (PDF), Matematikai Lapok 11: 264–274.
- ↑ Cooper, Colin; Dyer, Martin; Greenhill, Catherine (2007), "Sampling regular graphs and a peer-to-peer network", Combinatorics, Probability and Computing 16 (4): 557–593, doi:10.1017/S0963548306007978, MR 2334585.