Graph homomorphism
In the mathematical field of graph theory a graph homomorphism is a mapping between two graphs that respects their structure. More concretely it maps adjacent vertices to adjacent vertices.
Definitions
A graph homomorphism  from a graph
from a graph  to a graph
to a graph 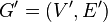 , written
, written 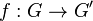 , is a mapping
, is a mapping
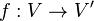 from the vertex set of
from the vertex set of  to the vertex set of
to the vertex set of  such that
such that 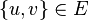 implies
implies 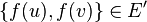 .
.
The above definition is extended to directed graphs. Then, for a homomorphism 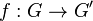 ,
, 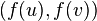 is an arc of
is an arc of  if
if  is an arc of
is an arc of  .
.
If there exists a homomorphism 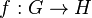 we shall write
we shall write 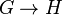 , and
, and 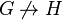 otherwise. If
otherwise. If 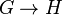 ,
,  is said to be homomorphic to
is said to be homomorphic to  or
or  -colourable.
-colourable.
If the homomorphism 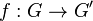 is a bijection whose inverse function is also a graph homomorphism, then
is a bijection whose inverse function is also a graph homomorphism, then  is a graph isomorphism.
is a graph isomorphism.
Two graphs  and
and  are homomorphically equivalent if
are homomorphically equivalent if
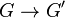 and
and 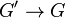 .
.
A retract of a graph  is a subgraph
is a subgraph  of
of  such that there exists a homomorphism
such that there exists a homomorphism 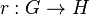 , called retraction with
, called retraction with 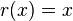 for any vertex
for any vertex  of
of  . A core is a graph which does not retract to a proper subgraph. Any graph is homomorphically equivalent to a unique core.
. A core is a graph which does not retract to a proper subgraph. Any graph is homomorphically equivalent to a unique core.
Properties
The composition of homomorphisms are homomorphisms.
Graph homomorphism preserves connectedness.
The tensor product of graphs is the category-theoretic product for the category of graphs and graph homomorphisms.
Connection to coloring and girth
A graph coloring is an assignment of one of k colors to each vertex of a graph G so that the endpoints of each edge have different colors, for some number k. Any coloring corresponds to a homomorphism 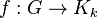 from G to a complete graph Kk: the vertices of Kk correspond to the colors of G, and f maps each vertex of G with color c to the vertex of Kk that corresponds to c. This is a valid homomorphism because the endpoints of each edge of G are mapped to distinct vertices of Kk, and every two distinct vertices of Kk are connected by an edge, so every edge in G is mapped to an adjacent pair of vertices in Kk. Conversely if f is a homomorphism from G to Kk, then one can color G by using the same color for two vertices in G whenever they are both mapped to the same vertex in Kk. Because Kk has no edges that connect a vertex to itself, it is not possible for two adjacent vertices in G to both be mapped to the same vertex in Kk, so this gives a valid coloring. That is, G has a k-coloring if and only if it has a homomorphism to Kk.
from G to a complete graph Kk: the vertices of Kk correspond to the colors of G, and f maps each vertex of G with color c to the vertex of Kk that corresponds to c. This is a valid homomorphism because the endpoints of each edge of G are mapped to distinct vertices of Kk, and every two distinct vertices of Kk are connected by an edge, so every edge in G is mapped to an adjacent pair of vertices in Kk. Conversely if f is a homomorphism from G to Kk, then one can color G by using the same color for two vertices in G whenever they are both mapped to the same vertex in Kk. Because Kk has no edges that connect a vertex to itself, it is not possible for two adjacent vertices in G to both be mapped to the same vertex in Kk, so this gives a valid coloring. That is, G has a k-coloring if and only if it has a homomorphism to Kk.
If there are two homomorphisms 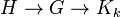 , then their composition
, then their composition 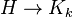 is also a homomorphism. In other words, if a graph G can be colored with k colors, and there is a homomorphism
is also a homomorphism. In other words, if a graph G can be colored with k colors, and there is a homomorphism 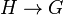 , then H can also be k-colored. Therefore, whenever a homomorphism
, then H can also be k-colored. Therefore, whenever a homomorphism 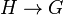 exists, the chromatic number of H is less than or equal to the chromatic number of G.
exists, the chromatic number of H is less than or equal to the chromatic number of G.
Homomorphisms can also be used very similarly to characterize the odd girth of a graph G, the length of its shortest odd-length cycle.
The odd girth is, equivalently, the smallest odd number g for which there exists a homomorphism 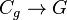 . For this reason, if
. For this reason, if 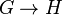 , then the odd girth of G is greater than or equal to the corresponding invariant of H.[1]
, then the odd girth of G is greater than or equal to the corresponding invariant of H.[1]
Complexity
The associated decision problem, i.e. deciding whether there exists a homomorphism from one graph to another, is NP-complete. Determining whether there is an isomorphism between two graphs is also an important problem in computational complexity theory; see graph isomorphism problem.
See also
- Hadwiger's conjecture.
- Graph rewriting
- Median graphs, definable as the retracts of hypercubes.
Notes
- ↑ Hell & Nešetřil (2004), p. 7.
References
- Hell, Pavol; Nešetřil, Jaroslav (2004), Graphs and Homomorphisms (Oxford Lecture Series in Mathematics and Its Applications), Oxford University Press, ISBN 0-19-852817-5
- Brown, R.; Morris, I.; Shrimpton, J.; Wensley, C. D. (2008), "Graphs of morphisms of graphs", Electronic Journal of Combinatorics 15 (1): A1