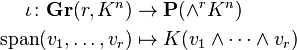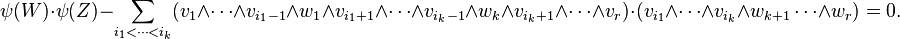Plücker embedding

This article is about the general Plücker embedding. For the classical case of 2-planes in 4-space, see Plücker coordinates.

In mathematics, the Plücker embedding is a method to realize the Grassmannian of all r-dimensional subspaces of an n-dimensional vector space V as a subvariety of the projective space of the rth exterior power of that vector space, P(∧^r V).

The Plücker embedding was first defined, in the case r = 2, n = 4, in coordinates by Julius Plücker as a way of describing the lines in three-dimensional space (which, as projective lines in real projective space, correspond to two-dimensional subspaces of a four-dimensional vector space). This was generalized by Hermann Grassmann to arbitrary r and n using a generalization of Plücker's coordinates, sometimes called Grassmann coordinates.

Definition

The Plücker embedding (over the field K) is the map ι defined by

\begin{align} \iota \colon \mathbf{Gr}(r, K^n) &{}\rightarrow \mathbf{P}(\wedge^r K^n)\\ \operatorname{span}( v_1, \ldots, v_r ) &{}\mapsto K( v_1 \wedge \cdots \wedge v_r ) \end{align}

where Gr(r, Kⁿ) is the Grassmannian, i.e., the space of all r-dimensional subspaces of the n-dimensional vector space, Kⁿ.

This is an isomorphism from the Grassmannian to the image of ι, which is a projective variety. This variety can be completely characterized as an intersection of quadrics, each coming from a relation on the Plücker (or Grassmann) coordinates that derives from linear algebra.

The bracket ring appears as the ring of polynomial functions on the exterior power.^[1]

Plücker relations

The embedding of the Grassmannian satisfies some very simple quadratic polynomials called the Plücker relations. These show that the Grassmannian embeds as an algebraic subvariety of $P (\land r V)$ and give another method of constructing the Grassmannian. To state the Plücker relations, choose two $r$ -dimensional subspaces $W$ and $Z$ of $V$ with bases ${w 1, ..., w r},$ and ${z 1, ..., z r},$ respectively. Then, for any integer $k \geq 0$ , the following equation is true in the homogeneous coordinate ring of $P (\land r V)$ :

\psi(W)\cdot\psi(Z) - \sum_{i_1 < \cdots < i_k} (v_1 \wedge \cdots \wedge v_{i_1 - 1} \wedge w_1 \wedge v_{i_1 + 1} \wedge \cdots \wedge v_{i_k - 1} \wedge w_k \wedge v_{i_k + 1} \wedge \cdots \wedge v_r)\cdot(v_{i_1} \wedge \cdots \wedge v_{i_k} \wedge w_{k+1} \cdots \wedge w_r) = 0.

When $dim(V) = 4$ , and $r = 2$ , the simplest Grassmannian which is not a projective space, the above reduces to a single equation. Denoting the coordinates of $P (\land r V)$ by $X 1,2, X 1,3, X 1,4, X 2,3, X 2,4, X 3,4$ , we have that $Gr (2, V)$ is defined by the equation

X 1,2 X 3,4 - X 1,3 X 2,4 + X 2,3 X 1,4 = 0.

In general, however, many more equations are needed to define the Plücker embedding of a Grassmannian in projective space.

References

↑ Björner, Anders; Las Vergnas, Michel; Sturmfels, Bernd; White, Neil; Ziegler, Günter (1999), Oriented matroids, Encyclopedia of Mathematics and Its Applications 46 (2nd ed.), Cambridge University Press, p. 79, ISBN 0-521-77750-X, Zbl 0944.52006

Griffiths, Phillip; Harris, Joseph (1994), Principles of algebraic geometry, Wiley Classics Library (2nd ed.), New York: John Wiley & Sons, ISBN 0-471-05059-8, MR 1288523, Zbl 0836.14001

Plücker embedding

Definition

Plücker relations

References

Further reading