4 21 polytope
| Orthogonal projections in E6 Coxeter plane | ||
|---|---|---|
 421 |
 142 |
 241 |
 Rectified 421 |
 Rectified 142 |
 Rectified 241 |
 Birectified 421 |
 Trirectified 421 | |
In 8-dimensional geometry, the 421 is a semiregular uniform 8-polytope, constructed within the symmetry of the E8 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 8-ic semi-regular figure.[1]
Its Coxeter symbol is 421, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 4-node sequences, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The rectified 421 is constructed by points at the mid-edges of the 421. The birectified 421 is constructed by points at the triangle face centers of the 421. The trirectified 421 is constructed by points at the tetrahedral centers of the 421, and is the same as the rectified 142.
These polytopes are part of a family of 255 = 28 − 1 convex uniform 8-polytopes, made of uniform 7-polytope facets and vertex figures, defined by all permutations of one or more rings in this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
421 polytope
| 421 | |
|---|---|
| Type | Uniform 8-polytope |
| Family | k21 polytope |
| Schläfli symbol | {3,3,3,3,32,1} |
| Coxeter symbol | 421 |
| Coxeter diagram | |
| 7-faces | 19440 total: 2160 411 17280 {36} |
| 6-faces | 207360: 138240 {35} 69120 {35} |
| 5-faces | 483840 {34} |
| 4-faces | 483840 {33} |
| Cells | 241920 {3,3} |
| Faces | 60480 {3} |
| Edges | 6720 |
| Vertices | 240 |
| Vertex figure | 321 polytope |
| Petrie polygon | 30-gon |
| Coxeter group | E8, [34,2,1] |
| Properties | convex |
The 421 is composed of 17,280 7-simplex and 2,160 7-orthoplex facets. Its vertex figure is the 321 polytope.
For visualization this 8-dimensional polytope is often displayed in a special skewed orthographic projection direction that fits its 240 vertices within a regular triacontagon (called a Petrie polygon). Its 6720 edges are drawn between the 240 vertices. Specific higher elements (faces, cells, etc.) can also be extracted and drawn on this projection.
As its 240 vertices represent the root vectors of the simple Lie group E8, the polytope is sometimes referred to as the E8 polytope.
The vertices of this polytope can be obtained by taking the 240 integral octonions of norm 1. Because the octonions are a nonassociative normed division algebra, these 240 points have a multiplication operation making them not into a group but rather a loop, in fact a Moufang loop.
Alternate names
- This polytope was discovered by Thorold Gosset, who described it in his 1900 paper as an 8-ic semi-regular figure.[1] It is the last finite semiregular figure in his enumeration, semiregular to him meaning that it contained only regular facets.
- E. L. Elte named it V240 (for its 240 vertices) in his 1912 listing of semiregular polytopes.[2]
- H.S.M. Coxeter called it 421 because its Coxeter-Dynkin diagram has three branches of length 4, 2, and 1, with a single node on the terminal node of the 4 branch.
- Dischiliahectohexaconta-myriaheptachiliadiacosioctaconta-zetton (Acronym Fy) - 2160-17280 facetted polyzetton (Jonathan Bowers)[3]
Coordinates
It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 8-dimensional space.
The 240 vertices of the 421 polytope can be constructed in two sets: 112 (22×8C2) with coordinates obtained from  by taking an arbitrary combination of signs and an arbitrary permutation of coordinates, and 128 roots (27) with coordinates obtained from
by taking an arbitrary combination of signs and an arbitrary permutation of coordinates, and 128 roots (27) with coordinates obtained from 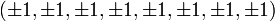 by taking an even number of minus signs (or, equivalently, requiring that the sum of all the eight coordinates be a multiple of 4).
by taking an even number of minus signs (or, equivalently, requiring that the sum of all the eight coordinates be a multiple of 4).
Each vertex has 56 nearest neighbors; for example, the nearest neighbors of the vertex  are those whose coordinates sum to 4, namely the 28 obtained by permuting the coordinates of
are those whose coordinates sum to 4, namely the 28 obtained by permuting the coordinates of  and the 28 obtained by permuting the coordinates of
and the 28 obtained by permuting the coordinates of  . These 56 points are the vertices of a 321 polytope in 7 dimensions.
. These 56 points are the vertices of a 321 polytope in 7 dimensions.
Each vertex has 126 second nearest neighbors: for example, the nearest neighbors of the vertex  are those whose coordinates sum to 0, namely the 56 obtained by permuting the coordinates of
are those whose coordinates sum to 0, namely the 56 obtained by permuting the coordinates of  and the 70 obtained by permuting the coordinates of
and the 70 obtained by permuting the coordinates of  . These 126 points are the vertices of a 231 polytope in 7 dimensions.
. These 126 points are the vertices of a 231 polytope in 7 dimensions.
Each vertex also has 56 third nearest neighbors, which are the negatives of its nearest neighbors, and one antipodal vertex, for a total of  vertices.
vertices.
Tessellations
This polytope is the vertex figure for a uniform tessellation of 8-dimensional space, represented by symbol 521 and Coxeter-Dynkin diagram:
Construction and faces
The facet information of this polytope can be extracted from its Coxeter-Dynkin diagram:
Removing the node on the short branch leaves the 7-simplex:
Removing the node on the end of the 2-length branch leaves the 7-orthoplex in its alternated form (411):
Every 7-simplex facet touches only 7-orthoplex facets, while alternate facets of an orthoplex facet touch either a simplex or another orthoplex. There are 17,280 simplex facets and 2160 orthoplex facets.
Since every 7-simplex has 7 6-simplex facets, each incident to no other 6-simplex, the 421 polytope has 120,960 (7×17,280) 6-simplex faces that are facets of 7-simplexes. Since every 7-orthoplex has 128 (27) 6-simplex facets, half of which are not incident to 7-simplexes, the 421 polytope has 138,240 (26×2160) 6-simplex faces that are not facets of 7-simplexes. The 421 polytope thus has two kinds of 6-simplex faces, not interchanged by symmetries of this polytope. The total number of 6-simplex faces is 259200 (120,960+138,240).
The vertex figure of a single-ring polytope is obtained by removing the ringed node and ringing its neighbor(s). This makes the 321 polytope.
Projections
 The 421 graph created as string art. |
 E8 Coxeter plane projection |
3D
 Mathematical representation of the physical Zome model isomorphic (?) to E8. This is constructed from VisibLie_E8 pictured with all 3360 edges of length √2(√5-1) from two concentric 600-cells (at the golden ratio) with orthogonal projections to perspective 3-space |
 The actual split real even E8 421 polytope projected into perspective 3-space pictured with all 6720 edges of length √2[4] |
2D
These graphs represent orthographic projections in the E8,E7,E6, and B8,D8,D7,D6,D5,D4,D3,A7,A5 Coxeter planes. The vertex colors are by overlapping multiplicity in the projection: colored by increasing order of multiplicities as red, orange, yellow, green.
| E8 / H4 [30] |
[20] | [24] |
|---|---|---|
 (Colors: 1) |
 (Colors: 1) |
 (Colors: 1) |
| E7 [18] |
E6 / F4 [12] |
[6] |
 (Colors: 1,3,6) |
 (Colors: 1,8,24) |
 (Colors: 1,2,3) |
| D3 / B2 / A3 [4] |
D4 / B3 / A2 / G2 [6] |
D5 / B4 [8] |
|---|---|---|
 (Colors: 1,12,32,60) |
 (Colors: 1,27,72) |
 (Colors: 1,8,24) |
| D6 / B5 / A4 [10] |
D7 / B6 [12] |
D8 / B7 / A6 [14] |
 (Colors: 1,5,10,20) |
 (Colors: 1,3,9,12) |
 (Colors: 1,2,3) |
| B8 [16/2] |
A5 [6] |
A7 [8] |
 (Colors: 1) |
 (Colors: 3,8,24,30) |
 (Colors: 1,2,4,8) |
k21 family
The 421 polytope is last in a family called the k21 polytopes. The first polytope in this family is the semiregular triangular prism which is constructed from three squares (2-orthoplexes) and two triangles (2-simplexes).
Geometric folding
The 421 is related to the 600-cell by a geometric folding of the Coxeter-Dynkin diagrams. This can be seen in the E8/H4 Coxeter plane projections. The 240 vertices of the 421 polytope are projected into 4-space as two copies of the 120 vertices of the 600-cell, one copy smaller than the other with the same orientation. Seen as a 2D orthographic projection in the E8/H4 Coxeter plane, the 120 vertices of the 600-cell are projected in the same four rings as seen in the 421. The other 4 rings of the 421 graph also match a smaller copy of the four rings of the 600-cell.
| E8/H4 Coxeter planes | |
|---|---|
| E8 |
H4 |
 421 |
 600-cell |
| [20] symmetry planes | |
 421 |
 600-cell |
Related polytopes
Using a complex number coordinate system, it can also be constructed as a 4-dimensional regular complex polytope, named as: 3{3}3{3}3{3}3. Coxeter called it the Witting polytope, after Alexander Witting.[6]
The 421 is sixth in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes.
| Space | Finite | Euclidean | Hyperbolic | |||||
|---|---|---|---|---|---|---|---|---|
| En | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Coxeter group |
E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 =  = E8+ = E8+ |
E10 =  = E8++ = E8++ |
| Coxeter diagram |
||||||||
| Symmetry | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] |
| Order | 12 | 120 | 192 | 51,840 | 2,903,040 | 696,729,600 | ∞ | |
| Graph |  |
 |
 |
 |
 |
 |
- | - |
| Name | −121 | 021 | 121 | 221 | 321 | 421 | 521 | 621 |
Rectified 4_21 polytope
| Rectified 421 | |
|---|---|
| Type | Uniform 8-polytope |
| Schläfli symbol | t1{3,3,3,3,32,1} |
| Coxeter symbol | t1(421) |
| Coxeter diagram | |
| 7-faces | 19680 total: |
| 6-faces | 375840 |
| 5-faces | 1935360 |
| 4-faces | 3386880 |
| Cells | 2661120 |
| Faces | 1028160 |
| Edges | 181440 |
| Vertices | 6720 |
| Vertex figure | 221 prism |
| Coxeter group | E8, [34,2,1] |
| Properties | convex |
The rectified 421 can be seen as a rectification of the 421 polytope, creating new vertices on the center of edges of the 421.
Alternative names
- Rectified dischiliahectohexaconta-myriaheptachiliadiacosioctaconta-zetton for rectified 2160-17280 polyzetton (Acronym riffy) (Jonathan Bowers)[7]
Construction
It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 8-dimensional space. It is named for being a rectification of the 421. Vertices are positioned at the midpoint of all the edges of 421, and new edges connecting them.
The facet information can be extracted from its Coxeter-Dynkin diagram.
Removing the node on the short branch leaves the rectified 7-simplex:
Removing the node on the end of the 2-length branch leaves the rectified 7-orthoplex in its alternated form:
Removing the node on the end of the 4-length branch leaves the 321:
The vertex figure is determined by removing the ringed node and adding a ring to the neighboring node. This makes a 221 prism.
Projections
2D
These graphs represent orthographic projections in the E8,E7,E6, and B8,D8,D7,D6,D5,D4,D3,A7,A5 Coxeter planes. The vertex colors are by overlapping multiplicity in the projection: colored by increasing order of multiplicities as red, orange, yellow, green.
| E8 / H4 [30] |
[20] | [24] |
|---|---|---|
 |
 |
 |
| E7 [18] |
E6 / F4 [12] |
[6] |
 |
 |
 |
| D3 / B2 / A3 [4] |
D4 / B3 / A2 / G2 [6] |
D5 / B4 [8] |
|---|---|---|
 |
 |
 |
| D6 / B5 / A4 [10] |
D7 / B6 [12] |
D8 / B7 / A6 [14] |
 |
 |
 |
| B8 [16/2] |
A5 [6] |
A7 [8] |
 |
 |
 |
Birectified 4_21 polytope
| Birectified 421 polytope | |
|---|---|
| Type | Uniform 8-polytope |
| Schläfli symbol | t2{3,3,3,3,32,1} |
| Coxeter symbol | t2(421) |
| Coxeter diagram | |
| 7-faces | 19680 total: |
| 6-faces | 382560 |
| 5-faces | 2600640 |
| 4-faces | 7741440 |
| Cells | 9918720 |
| Faces | 5806080 |
| Edges | 1451520 |
| Vertices | 60480 |
| Vertex figure | 5-demicube-triangular duoprism |
| Coxeter group | E8, [34,2,1] |
| Properties | convex |
The birectified 421can be seen as a second rectification of the uniform 421 polytope. Vertices of this polytope are positioned at the centers of all the 60480 triangular faces of the 421.
Alternative names
- Birectified dischiliahectohexaconta-myriaheptachiliadiacosioctaconta-zetton for birectified 2160-17280 polyzetton (acronym borfy) (Jonathan Bowers)[8]
Construction
It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 8-dimensional space. It is named for being a birectification of the 421. Vertices are positioned at the center of all the triangle faces of 421.
The facet information can be extracted from its Coxeter-Dynkin diagram.
Removing the node on the short branch leaves the birectified 7-simplex. There are 17280 of these facets.
Removing the node on the end of the 2-length branch leaves the birectified 7-orthoplex in its alternated form. There are 2160 of these facets.
Removing the node on the end of the 4-length branch leaves the rectified 321. There are 240 of these facets.
The vertex figure is determined by removing the ringed node and adding rings to the neighboring nodes. This makes a 5-demicube-triangular duoprism.
Projections
2D
These graphs represent orthographic projections in the E8,E7,E6, and B8,D8,D7,D6,D5,D4,D3,A7,A5 Coxeter planes. Edges are not drawn. The vertex colors are by overlapping multiplicity in the projection: colored by increasing order of multiplicities as red, orange, yellow, green, etc.
| E8 / H4 [30] |
[20] | [24] |
|---|---|---|
 |
 |
 |
| E7 [18] |
E6 / F4 [12] |
[6] |
 |
 |
 |
| D3 / B2 / A3 [4] |
D4 / B3 / A2 / G2 [6] |
D5 / B4 [8] |
|---|---|---|
 |
 |
 |
| D6 / B5 / A4 [10] |
D7 / B6 [12] |
D8 / B7 / A6 [14] |
 |
 |
 |
| B8 [16/2] |
A5 [6] |
A7 [8] |
 |
 |
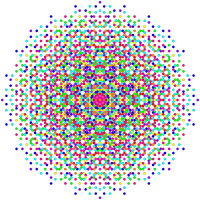 |
Trirectified 4_21 polytope
| Trirectified 421 polytope | |
|---|---|
| Type | Uniform 8-polytope |
| Schläfli symbol | t3{3,3,3,3,32,1} |
| Coxeter symbol | t3(421) |
| Coxeter diagram | |
| 7-faces | 19680 |
| 6-faces | 382560 |
| 5-faces | 2661120 |
| 4-faces | 9313920 |
| Cells | 16934400 |
| Faces | 14515200 |
| Edges | 4838400 |
| Vertices | 241920 |
| Vertex figure | tetrahedron-rectified 5-cell duoprism |
| Coxeter group | E8, [34,2,1] |
| Properties | convex |
Alternative names
- Trirectified dischiliahectohexaconta-myriaheptachiliadiacosioctaconta-zetton for trirectified 2160-17280 polyzetton (acronym torfy) (Jonathan Bowers)[9]
Construction
It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 8-dimensional space. It is named for being a birectification of the 421. Vertices are positioned at the center of all the triangle faces of 421.
The facet information can be extracted from its Coxeter-Dynkin diagram.
Removing the node on the short branch leaves the trirectified 7-simplex:
Removing the node on the end of the 2-length branch leaves the trirectified 7-orthoplex in its alternated form:
Removing the node on the end of the 4-length branch leaves the birectified 321:
The vertex figure is determined by removing the ringed node and ring the neighbor nodes. This makes a tetrahedron-rectified 5-cell duoprism.
Projections
2D
These graphs represent orthographic projections in the E7,E6, and B8,D8,D7,D6,D5,D4,D3,A7,A5 Coxeter planes. The vertex colors are by overlapping multiplicity in the projection: colored by increasing order of multiplicities as red, orange, yellow, green.
(E8 and B8 were too large to display)
| E7 [18] |
E6 / F4 [12] |
D4 - E6 [6] |
|---|---|---|
 |
 |
 |
| D3 / B2 / A3 [4] |
D4 / B3 / A2 / G2 [6] |
D5 / B4 [8] |
|---|---|---|
 |
 |
 |
| D6 / B5 / A4 [10] |
D7 / B6 [12] |
D8 / B7 / A6 [14] |
 |
 | |
| A5 [6] |
A7 [8] | |
 |
 |
See also
Notes
- 1 2 Gosset, 1900
- ↑ Elte, 1912
- ↑ Klitzing, (o3o3o3o *c3o3o3o3x - fy)
- ↑ e8Flyer.nb
- ↑ David Richter: Gosset's Figure in 8 Dimensions, A Zome Model
- ↑ Coxeter Regular Convex Polytopes, 12.5 The Witting polytope
- ↑ Klitzing, (o3o3o3o *c3o3o3x3o - riffy)
- ↑ Klitzing, (o3o3o3o *c3o3x3o3o - borfy)
- ↑ Klitzing, (o3o3o3o *c3x3o3o3o - torfy)
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen
- Coxeter, H. S. M., Regular Complex Polytopes, Cambridge University Press, (1974).
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45] See p347 (figure 3.8c) by Peter McMullen: (30-gonal node-edge graph of 421)
- Richard Klitzing, 8D, uniform polytopes (polyzetta) o3o3o3o *c3o3o3o3x - fy, o3o3o3o *c3o3o3x3o - riffy, o3o3o3o *c3o3x3o3o - borfy, o3o3o3o *c3x3o3o3o - torfy
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
