Gorenstein ring
In commutative algebra, a Gorenstein local ring is a Noetherian commutative local ring R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition.
Gorenstein rings were introduced by Grothendieck in his 1961 seminar (published in (Hartschorne 1967)), who named them because of their relation to a duality property of singular plane curves studied by Gorenstein (1952) (who was fond of claiming that he did not understand the definition of a Gorenstein ring). The zero-dimensional case had been studied by Macaulay (1934). Serre (1961) and Bass (1963) publicized the concept of Gorenstein rings.
Noncommutative analogues of 0-dimensional Gorenstein rings are called Frobenius rings.
For Noetherian local rings, there is the following chain of inclusions.
- Universally catenary rings ⊃ Cohen–Macaulay rings ⊃ Gorenstein rings ⊃ complete intersection rings ⊃ regular local rings
Definitions
A Gorenstein ring is a commutative ring such that each localization at a prime ideal is a Gorenstein local ring. The Gorenstein ring concept is a special case of the more general Cohen–Macaulay ring.
The classical definition reads:
A local Cohen–Macaulay ring R is called Gorenstein if there is a maximal R-regular sequence in the maximal ideal generating an irreducible ideal.
For a Noetherian commutative local ring 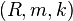 of Krull dimension
of Krull dimension  , the following are equivalent:
, the following are equivalent:
-
 has finite injective dimension as an
has finite injective dimension as an  -module;
-module; -
 has injective dimension
has injective dimension  as an
as an  -module;
-module; -
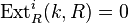 for
for 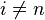 and
and 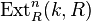 is isomorphic to
is isomorphic to  ;
; -
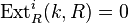 for some
for some  ;
; -
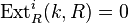 for all
for all  and
and 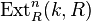 is isomorphic to
is isomorphic to  ;
; -
 is an
is an  -dimensional Gorenstein ring.
-dimensional Gorenstein ring.
A (not necessarily commutative) ring R is called Gorenstein if R has finite injective dimension both as a left R-module and as a right R-module. If R is a local ring, we say R is a local Gorenstein ring.
Examples
- Every local complete intersection ring, in particular every regular local ring, is Gorenstein.
- The ring k[x,y,z]/(x2, y2, xz, yz, z2–xy) is a 0-dimensional Gorenstein ring that is not a complete intersection ring.
- The ring k[x,y]/(x2, y2, xy) is a 0-dimensional Cohen–Macaulay ring that is not a Gorenstein ring.
Properties
A noetherian commutative local ring is Gorenstein if and only if its completion is Gorenstein.[1]
The canonical module of a graded Gorenstein ring R is isomorphic to R with some degree shift.
References
- Bass, Hyman (1963), "On the ubiquity of Gorenstein rings", Mathematische Zeitschrift 82: 8–28, doi:10.1007/BF01112819, ISSN 0025-5874, MR 0153708
- Bruns, Winfried; Herzog, Jürgen (1993), Cohen-Macaulay rings, Cambridge Studies in Advanced Mathematics 39, Cambridge University Press, ISBN 978-0-521-41068-7, MR 1251956
- Gorenstein, D. (1952), "An arithmetic theory of adjoint plane curves", Transactions of the American Mathematical Society 72: 414–436, doi:10.2307/1990710, ISSN 0002-9947, MR 0049591
- Grothendieck, Alexandre (1957), "Théorèmes de dualité pour les faisceaux algébriques cohérents", Séminaire Bourbaki, Vol. 4, Paris: Société Mathématique de France, pp. 169–193, MR 1610898
- Hartshorne, Robin (1967), Local cohomology. A seminar given by A. Grothendieck, Harvard University, Fall, 1961, Lecture Notes in Mathematics 41, Berlin-New York: Springer-Verlag, MR 0224620
- Hazewinkel, Michiel, ed. (2001), "Gorenstein_ring", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Macaulay, F. S. (1934), "Modern algebra and polynomial ideals", Mathematical Proceedings of the Cambridge Philosophical Society 30 (1): 27–46, doi:10.1017/S0305004100012354, ISSN 0305-0041
- Hideyuki Matsumura, Commutative Ring Theory, Cambridge studies in advanced mathematics 8.
- Serre, Jean-Pierre (1961), Sur les modules projectifs, Séminaire Dubreil. Algèbre et théorie des nombres 14, pp. 1–16