Good cover (algebraic topology)
In mathematics, an open cover of a topological space  is a family of open subsets such that
is a family of open subsets such that  is the union of all of the open sets. In algebraic topology, an open cover is called a good cover if all open sets in the cover and all intersections of finitely many open sets,
is the union of all of the open sets. In algebraic topology, an open cover is called a good cover if all open sets in the cover and all intersections of finitely many open sets, 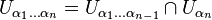 , are contractible (Petersen 2006).
, are contractible (Petersen 2006).
The concept was introduced by Andre Weil in 1952 for differential manifolds, demanding the 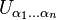 to be differentiably contractible.
A modern version of this definition appears in Bott & Tu (1982).
to be differentiably contractible.
A modern version of this definition appears in Bott & Tu (1982).
Application
A major reason for the notion of a good cover is that the Leray spectral sequence of a fiber bundle degenerates for a good cover, and so the Čech cohomology associated with a good cover is the same as the Čech cohomology of the space. (Such a cover is known as a Leray cover.)
Example
The two-dimensional surface of a sphere 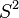 has an open cover by two contractible sets, open neighborhoods of opposite hemispheres. However these two sets have an intersection that forms a non-contractible equatorial band. To form a good cover for this surface, one needs at least four open sets. A good cover can be formed by projecting the faces of a tetrahedron onto a sphere in which it is inscribed, and taking an open neighborhood of each face.
has an open cover by two contractible sets, open neighborhoods of opposite hemispheres. However these two sets have an intersection that forms a non-contractible equatorial band. To form a good cover for this surface, one needs at least four open sets. A good cover can be formed by projecting the faces of a tetrahedron onto a sphere in which it is inscribed, and taking an open neighborhood of each face.
References
- Bott, Raoul; Tu, Loring (1982), Differential Forms in Algebraic Topology, New York: Springer, ISBN 0-387-90613-4, §5, S. 42.
- Weil, Andre (1952), "Sur les theoremes de de Rham", Commentarii Math. Helv., 26 \ pages = 119-145
- Petersen, Peter (2006), Riemannian geometry, Graduate Texts in Mathematics 171 (2nd ed.), New York: Springer, p. 383, ISBN 978-0387-29246-5, MR 2243772