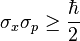Hidden variable theory

Quantum mechanics
Uncertainty principle
Introduction Glossary History
Background Classical mechanics Old quantum theory Bra–ket notation Hamiltonian Interference
Fundamentals Complementarity Decoherence Entanglement Energy level Measurement Nonlocality Quantum number State Superposition Symmetry Tunnelling Uncertainty Wave function (collapse)
Experiments Afshar Bell's inequality Davisson–Germer Double-slit Elitzur–Vaidman Franck–Hertz Mach–Zehnder Popper Quantum eraser (delayed-choice) Schrödinger's cat Stern–Gerlach Wheeler's delayed-choice
Formulations Overview Heisenberg Interaction Matrix Phase-space Schrödinger Sum-over-histories (path integral)
Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Overview Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Many-worlds Objective collapse Bayesian Quantum logic Relational Stochastic Scale relativity Transactional
Advanced topics Quantum chaos Quantum computing Density matrix Quantum field theory Fractional quantum mechanics Quantum information science Relativistic quantum mechanics Scattering theory Quantum statistical mechanics
Scientists Aharonov Bell Blackett Bloch Bohm Bohr Born Bose de Broglie Candlin Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Pauli Lamb Landau Laue Moseley Millikan Onnes Planck Rabi Raman Rydberg Schrödinger Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger

Historically, in physics, hidden variable theories were espoused by some physicists who argued that the state of a physical system, as formulated by quantum mechanics, does not give a complete description for the system; i.e., that quantum mechanics is ultimately incomplete, and that a complete theory would provide descriptive categories to account for all observable behavior and thus avoid any indeterminism. The existence of indeterminacy for some measurements is a characteristic of prevalent interpretations of quantum mechanics; moreover, bounds for indeterminacy can be expressed in a quantitative form by the Heisenberg uncertainty principle.

Albert Einstein, the most famous proponent of hidden variables, objected to the fundamentally probabilistic nature of quantum mechanics,^[1] and famously declared "I am convinced God does not play dice".^[2] Einstein, Podolsky, and Rosen argued that "elements of reality" (hidden variables) must be added to quantum mechanics to explain entanglement without action at a distance.^[3][4] Later, Bell's theorem would suggest that local hidden variables of certain types are impossible, or that they evolve non-locally. A famous non-local theory is De Broglie–Bohm theory.

Motivation

Under the standard Copenhagen interpretation, quantum mechanics is non-deterministic, meaning that it generally does not predict the outcome of any measurement with certainty. Instead, it indicates what the probabilities of the outcomes are, with the indeterminism of observable quantities constrained by the uncertainty principle. The question arises whether there might be some deeper reality hidden beneath quantum mechanics, to be described by a more fundamental theory that can always predict the outcome of each measurement with certainty: if the exact properties of every subatomic particle were known the entire system could be modeled exactly using deterministic physics similar to classical physics.

In other words, it is conceivable that the standard interpretation of quantum mechanics is an incomplete description of nature. The designation of variables as underlying "hidden" variables depends on the level of physical description (so, for example, "if a gas is described in terms of temperature, pressure, and volume, then the velocities of the individual atoms in the gas would be hidden variables".^[5]). Physicists supporting De Broglie–Bohm theory maintain that underlying the observed probabilistic nature of the universe is a deterministic objective foundation/property—the hidden variable. Others, however, believe that there is no deeper deterministic reality in quantum mechanics—experiments have shown a vast class of hidden variable theories to be incompatible with observations.

A lack of a kind of realism (understood here as asserting independent existence and evolution of physical quantities, such as position or momentum, without the process of measurement) is crucial in the Copenhagen interpretation. Realistic interpretations (which were already incorporated, to an extent, into the physics of Feynman^[6]), on the other hand, assume that particles have certain trajectories. Under such view, these trajectories will almost always be continuous, which follows both from the finitude of the perceived speed of light ("leaps" should rather be precluded) and, more importantly, from the principle of least action, as deduced in quantum physics by Dirac. But continuous movement, in accordance with the mathematical definition, implies deterministic movement for a range of time arguments;^[7] and thus realism is, under modern physics, one more reason for seeking (at least certain limited) determinism and thus a hidden variable theory (especially that such theory exists: see De Broglie–Bohm interpretation).

Although determinism was initially a major motivation for physicists looking for hidden variable theories, nondeterministic theories trying to explain what the supposed reality underlying the quantum mechanics formalism looks like are also considered hidden variable theories; for example Edward Nelson's stochastic mechanics.

"God does not play dice"

In June 1926, Max Born published a paper, "Zur Quantenmechanik der Stoßvorgänge" ("Quantum Mechanics of Collision Phenomena") in the scientific journal Zeitschrift für Physik, in which he was the first to clearly enunciate the probabilistic interpretation of the quantum wavefunction, which had been introduced by Erwin Schrödinger earlier in the year. Born concluded the paper as follows:

Here the whole problem of determinism comes up. From the standpoint of our quantum mechanics there is no quantity which in any individual case causally fixes the consequence of the collision; but also experimentally we have so far no reason to believe that there are some inner properties of the atom which conditions a definite outcome for the collision. Ought we to hope later to discover such properties ... and determine them in individual cases? Or ought we to believe that the agreement of theory and experiment—as to the impossibility of prescribing conditions for a causal evolution—is a pre-established harmony founded on the nonexistence of such conditions? I myself am inclined to give up determinism in the world of atoms. But that is a philosophical question for which physical arguments alone are not decisive.

Born's interpretation of the wavefunction was criticized by Schrödinger, who had previously attempted to interpret it in real physical terms, but Albert Einstein's response became one of the earliest and most famous assertions that quantum mechanics is incomplete:

Quantum mechanics is very worthy of regard. But an inner voice tells me that this is not yet the right track. The theory yields much, but it hardly brings us closer to the Old One's secrets. I, in any case, am convinced that He does not play dice.^[8][9]

Early attempts at hidden variable theories

Shortly after making his famous "God does not play dice" comment, Einstein attempted to formulate a deterministic counterproposal to quantum mechanics, presenting a paper at a meeting of the Academy of Sciences in Berlin, on 5 May 1927, titled "Bestimmt Schrödinger's Wellenmechanik die Bewegung eines Systems vollständig oder nur im Sinne der Statistik?" (“Does Schrödinger’s wave mechanics determine the motion of a system completely or only in the statistical sense?”).^[10] However, as the paper was being prepared for publication in the academy's journal, Einstein decided to withdraw it, possibly because he discovered that, contrary to his intention, it implied non-separability of entangled systems, which he regarded as absurd.^[11]

At the Fifth Solvay Congress, held in Belgium in October 1927 and attended by all the major theoretical physicists of the era, Louis de Broglie presented his own version of a deterministic hidden-variable theory, apparently unaware of Einstein's aborted attempt earlier in the year. In his theory, every particle had an associated, hidden "pilot wave" which served to guide its trajectory through space. The theory was subject to criticism at the Congress, particularly by Wolfgang Pauli, which de Broglie did not adequately answer. De Broglie abandoned the theory shortly thereafter.

Declaration of completeness of quantum mechanics

Also at the Fifth Solvay Congress, Max Born and Werner Heisenberg made a presentation summarizing the recent tremendous theoretical development of the subject. At the conclusion of the presentation, they declared:

[W]hile we consider ... a quantum mechanical treatment of the electromagnetic field ... as not yet finished, we consider quantum mechanics to be a closed theory, whose fundamental physical and mathematical assumptions are no longer susceptible of any modification.... On the question of the 'validity of the law of causality' we have this opinion: as long as one takes into account only experiments that lie in the domain of our currently acquired physical and quantum mechanical experience, the assumption of indeterminism in principle, here taken as fundamental, agrees with experience.^[12]

Bohr–Einstein debates

Although there is no record of Einstein responding to Born and Heisenberg during the technical sessions of the Fifth Solvay Congress, he did challenge the completeness of quantum mechanics during informal discussions over meals, presenting a thought experiment intended to demonstrate that quantum mechanics could not be entirely correct. He did likewise during the Sixth Solvay Congress held in 1930. Both times, Niels Bohr is generally considered to have successfully defended quantum mechanics by discovering errors in Einstein's arguments.

EPR paradox

The debates between Bohr and Einstein essentially concluded in 1935, when Einstein finally expressed what is widely considered his best argument against the completeness of quantum mechanics. Einstein, Podolsky, and Rosen had proposed their definition of a "complete" description as one which uniquely determines the values of all its measurable properties. Einstein later summarized their argument as follows:

Consider a mechanical system consisting of two partial systems A and B which interact with each other only during a limited time. Let the ψ function [i.e., wavefunction ] before their interaction be given. Then the Schrödinger equation will furnish the ψ function after the interaction has taken place. Let us now determine the physical state of the partial system A as completely as possible by measurements. Then quantum mechanics allows us to determine the ψ function of the partial system B from the measurements made, and from the ψ function of the total system. This determination, however, gives a result which depends upon which of the physical quantities (observables) of A have been measured (for instance, coordinates or momenta). Since there can be only one physical state of B after the interaction which cannot reasonably be considered to depend on the particular measurement we perform on the system A separated from B it may be concluded that the ψ function is not unambiguously coordinated to the physical state. This coordination of several ψ functions to the same physical state of system B shows again that the ψ function cannot be interpreted as a (complete) description of a physical state of a single system.^[13]

Bohr answered Einstein's challenge as follows:

[The argument of] Einstein, Podolsky and Rosen contains an ambiguity as regards the meaning of the expression "without in any way disturbing a system." ... [E]ven at this stage [i.e., the measurement of, for example, a particle that is part of an entangled pair], there is essentially the question of an influence on the very conditions which define the possible types of predictions regarding the future behavior of the system. Since these conditions constitute an inherent element of the description of any phenomenon to which the term "physical reality" can be properly attached, we see that the argumentation of the mentioned authors does not justify their conclusion that quantum-mechanical description is essentially incomplete."^[14]

Bohr is here choosing to define a "physical reality" as limited to a phenomenon that is immediately observable by an arbitrarily chosen and explicitly specified technique, using his own special definition of the term 'phenomenon'. He wrote in 1948:

As a more appropriate way of expression, one may strongly advocate limitation of the use of the word phenomenon to refer exclusively to observations obtained under specified circumstances, including an account of the whole experiment."^[15][16]

This was, of course, in conflict with the definition used by the EPR paper, as follows:

If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity. [Italics in original]^[3]

Bell's theorem

In 1964, John Bell showed through his famous theorem that if local hidden variables exist, certain experiments could be performed involving quantum entanglement where the result would satisfy a Bell inequality. If, on the other hand, statistical correlations resulting from quantum entanglement could not be explained by local hidden variables, the Bell inequality would be violated. Another no-go theorem concerning hidden variable theories is the Kochen–Specker theorem.

Physicists such as Alain Aspect and Paul Kwiat have performed experiments that have found violations of these inequalities up to 242 standard deviations^[17] (excellent scientific certainty). This rules out local hidden variable theories, but does not rule out non-local ones. Theoretically, there could be experimental problems that affect the validity of the experimental findings.

Gerard 't Hooft has disputed the validity of Bell's theorem on the basis of the superdeterminism loophole and proposed some ideas to construct local deterministic models.^[18]

Bohm's hidden variable theory

Assuming the validity of Bell's theorem, any deterministic hidden-variable theory which is consistent with quantum mechanics would have to be non-local, maintaining the existence of instantaneous or faster-than-light relations (correlations) between physically separated entities. The currently best-known hidden-variable theory, the "causal" interpretation of the physicist and philosopher David Bohm, originally published in 1952, is a non-local hidden variable theory. Bohm unknowingly rediscovered (and extended) the idea that Louis de Broglie had proposed in 1927 (and abandoned) – hence this theory is commonly called "de Broglie-Bohm theory". Bohm posited both the quantum particle, e.g. an electron, and a hidden 'guiding wave' that governs its motion. Thus, in this theory electrons are quite clearly particles—when a double-slit experiment is performed, its trajectory goes through one slit rather than the other. Also, the slit passed through is not random but is governed by the (hidden) guiding wave, resulting in the wave pattern that is observed.

Such a view does not contradict the idea of local events that is used in both classical atomism and relativity theory as Bohm's theory (and quantum mechanics) are still locally causal (that is, information travel is still restricted to the speed of light) but allow nonlocal correlations. It points to a view of a more holistic, mutually interpenetrating and interacting world. Indeed, Bohm himself stressed the holistic aspect of quantum theory in his later years, when he became interested in the ideas of Jiddu Krishnamurti.

In Bohm's interpretation, the (nonlocal) quantum potential constitutes an implicate (hidden) order which organizes a particle, and which may itself be the result of yet a further implicate order: a superimplicate order which organizes a field.^[19] Nowadays Bohm's theory is considered to be one of many interpretations of quantum mechanics which give a realist interpretation, and not merely a positivistic one, to quantum-mechanical calculations. Some consider it the simplest theory to explain quantum phenomena.^[20] Nevertheless, it is a hidden variable theory, and necessarily so.^[21] The major reference for Bohm's theory today is his book with Basil Hiley, published posthumously.^[22]

A possible weakness of Bohm's theory is that some (including Einstein, Pauli, and Heisenberg) feel that it looks contrived.^[23] (Indeed, Bohm thought this of his original formulation of the theory.^[24]) It was deliberately designed to give predictions that are in all details identical to conventional quantum mechanics.^[24] Bohm's original aim was not to make a serious counterproposal but simply to demonstrate that hidden-variable theories are indeed possible.^[24] (It thus provided a supposed counterexample to the famous proof by John von Neumann that was generally believed to demonstrate that no deterministic theory reproducing the statistical predictions of quantum mechanics is possible.) Bohm said he considered his theory to be unacceptable as a physical theory due to the guiding wave's existence in an abstract multi-dimensional configuration space, rather than three-dimensional space.^[24] His hope was that the theory would lead to new insights and experiments that would lead ultimately to an acceptable one;^[24] his aim was not to set out a deterministic, mechanical viewpoint, but rather to show that it was possible to attribute properties to an underlying reality, in contrast to the conventional approach to quantum mechanics.^[25]

Recent developments

In August 2011, Roger Colbeck and Renato Renner published a proof that any extension of quantum mechanical theory, whether using hidden variables or otherwise, cannot provide a more accurate prediction of outcomes, assuming that observers can freely choose the measurement settings.^[26] Colbeck and Renner write: "In the present work, we have ... excluded the possibility that any extension of quantum theory (not necessarily in the form of local hidden variables) can help predict the outcomes of any measurement on any quantum state. In this sense, we show the following: under the assumption that measurement settings can be chosen freely, quantum theory really is complete".

In January 2013, GianCarlo Ghirardi and Raffaele Romano described a model which, "under a different free choice assumption [...] violates [the statement by Colbeck and Renner] for almost all states of a bipartite two-level system, in a possibly experimentally testable way".^[27]

See also

• Local hidden variable theory
• Bell's theorem
• Bell test experiments
• Quantum mechanics
• Bohm interpretation
• Spekkens Toy Model

References

Bibliography

• Albert Einstein, Boris Podolsky, and Nathan Rosen, "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?" Physical Review 47, 777–780 (1935).
• John Stewart Bell, "On the Einstein–Podolsky–Rosen paradox", Physics 1, (1964) 195–200. Reprinted in Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press, 2004.
• D. Bohm and B. J. Hiley, The Undivided Universe, Routledge, 1993
• Wolfgang Pauli, letter to M. Fierz dated 10 August 1954, reprinted and translated in K. V. Laurikainen, Beyond the Atom: The Philosophical Thought of Wolfgang Pauli, Springer-Verlag, Berlin, 1988, p. 226.
• Werner Heisenberg, Physics and Beyond: Encounters and Conversations, translated by A. J. Pomerans, Harper & Row, New York, 1971, pp. 63–64.
• Claude Cohen-Tannoudji, Bernard Diu and Franck Laloë, Mecanique quantique (see also Quantum Mechanics translated from the French by Susan Hemley, Nicole Ostrowsky, and Dan Ostrowsky; John Wiley & Sons 1982) Hermann, Paris, France. 1977.
• P. S. Hanle, Indeterminacy before Heisenberg: The Case of Franz Exner and Erwin Schrödinger, Historical Studies in the Physical Sciences 10, 225 (1979).
• Asher Peres and Wojciech Zurek, "Is quantum theory universally valid?" American Journal of Physics 50, 807 (1982).
• Wojciech Zurek Physical Review D 26 1862. 1982.
• Max Jammer, "The EPR Problem in Its Historical Development", in Symposium on the Foundations of Modern Physics: 50 years of the Einstein–Podolsky–Rosen Gedankenexperiment, edited by P. Lahti and P. Mittelstaedt (World Scientific, Singapore, 1985), pp. 129–149.
• Arthur Fine, The Shaky Game: Einstein Realism and the Quantum Theory, University of Chicago Press, Chicago, 1986.
• Thomas Kuhn. Black-Body Theory and the Quantum Discontinuity, 1894–1912 Chicago University Press. 1987.
• Asher Peres, Quantum Theory: Concepts and Methods, Kluwer, Dordrecht, 1993.
• Carlton M. Caves and Christopher A. Fuchs, "Quantum Information: How Much Information in a State Vector?", in The Dilemma of Einstein, Podolsky and Rosen – 60 Years Later, edited by A. Mann and M. Revzen, Ann. Israel Physical Society 12, 226–257 (1996).
• Carlo Rovelli. "Relational quantum mechanics" International Journal of Theoretical Physics 35 1637–1678. 1996.
• Roland Omnès, Understanding Quantum Mechanics, Princeton University Press, 1999.
• Roman Jackiw and Daniel Kleppner, "One Hundred Years of Quantum Physics", Science, Vol. 289 Issue 5481, p. 893, August 2000.
• Orly Alter and Yoshihisa Yamamoto (2001). Quantum Measurement of a Single System (PDF). Wiley-Interscience. 136 pp. doi:10.1002/9783527617128. ISBN 9780471283089. Slides. 
• Erich Joos, et al., Decoherence and the Appearance of a Classical World in Quantum Theory, 2nd ed., Berlin, Springer, 2003.
• Wojciech Zurek (2003). "Decoherence and the transition from quantum to classical — Revisited", arXiv:quant-ph/0306072 (An updated version of Physics Today, 44:36–44 (1991) article)
• Wojciech Zurek, "Decoherence, einselection, and the quantum origins of the classical" in Reviews of Modern Physics, vol.75, (715).
• Asher Peres and Daniel Terno, "Quantum Information and Relativity Theory", Reviews of Modern Physics 76 (2004) 93.
• Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, Alfred Knopf 2004.
• Maximilian Schlosshauer, "Decoherence, the Measurement Problem, and Interpretations of Quantum Mechanics", in Reviews of Modern Physics, vol.76, pages 1267–1305, 2005.
• Federico Laudisa and Carlo Rovelli. "Relational Quantum Mechanics" The Stanford Encyclopedia of Philosophy (Fall 2005 Edition).
• Marco Genovese, "Research on hidden variable theories: a review of recent progresses", in Physics Reports, vol.413, 2005.

External links

• The David Bohm Society