Glide reflection


In 2-dimensional geometry, a glide reflection (or transflection) is a type of opposite isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line.
A single glide is represented as frieze group p11g. A glide reflection can be seen as a limiting rotoreflection, where the rotation becomes a translation. It can also be given a Schoenflies notation as S2∞, Coxeter notation as [∞+,2+], and orbifold notation as ∞×.
Description
The combination of a reflection in a line and a translation in a perpendicular direction is a reflection in a parallel line. However, a glide reflection cannot be reduced like that. Thus the effect of a reflection combined with any translation is a glide reflection, with as special case just a reflection. These are the two kinds of indirect isometries in 2D.
For example, there is an isometry consisting of the reflection on the x-axis, followed by translation of one unit parallel to it. In coordinates, it takes
- (x, y) → (x + 1, −y).
It fixes a system of parallel lines.
The isometry group generated by just a glide reflection is an infinite cyclic group.[1]
Combining two equal glide reflections gives a pure translation with a translation vector that is twice that of the glide reflection, so the even powers of the glide reflection form a translation group.
In the case of glide reflection symmetry, the symmetry group of an object contains a glide reflection, and hence the group generated by it. If that is all it contains, this type is frieze group p11g.
Example pattern with this symmetry group:
Frieze group nr. 6 (glide-reflections, translations and rotations) is generated by a glide reflection and a rotation about a point on the line of reflection. It is isomorphic to a semi-direct product of Z and C2.
Example pattern with this symmetry group:
A typical example of glide reflection in everyday life would be the track of footprints left in the sand by a person walking on a beach.
For any symmetry group containing some glide reflection symmetry, the translation vector of any glide reflection is one half of an element of the translation group. If the translation vector of a glide reflection is itself an element of the translation group, then the corresponding glide reflection symmetry reduces to a combination of reflection symmetry and translational symmetry.
Glide reflection symmetry with respect to two parallel lines with the same translation implies that there is also translational symmetry in the direction perpendicular to these lines, with a translation distance which is twice the distance between glide reflection lines. This corresponds to wallpaper group pg; with additional symmetry it occurs also in pmg, pgg and p4g.
If there are also true reflection lines in the same direction then they are evenly spaced between the glide reflection lines. A glide reflection line parallel to a true reflection line already implies this situation. This corresponds to wallpaper group cm. The translational symmetry is given by oblique translation vectors from one point on a true reflection line to two points on the next, supporting a rhombus with the true reflection line as one of the diagonals. With additional symmetry it occurs also in cmm, p3m1, p31m, p4m and p6m.
In 3D the glide reflection is called a glide plane. It is a reflection in a plane combined with a translation parallel to the plane.
Wallpaper groups
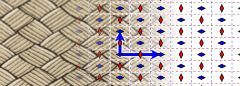
In the Euclidean plane 3 of 17 wallpaper groups require glide reflection generators. p2gg has orthogonal glide reflections and 2-fold rotations. cm has parallel mirrors and glides, and pg has parallel glides. (Glide reflections are shown below as dashed lines)
| p2gg (22×) | cm (*×) | pg (××) |
|---|---|---|
 |
 |
 |
 |
 |
 |
Glide reflection in nature and games
Glide symmetry can be observed in nature among certain fossils of the Ediacara biota; the machaeridians; and certain palaeoscolecid worms.[2]
Glide reflection is common in Conway's Game of Life.
See also
- Screw axis, glide plane for the corresponding 3D symmetry operations
References
- ↑ Martin, George E. (1982), Transformation Geometry: An Introduction to Symmetry, Undergraduate Texts in Mathematics, Springer, p. 64, ISBN 9780387906362.
- ↑ Waggoner, B. M. (1996). "Phylogenetic Hypotheses of the Relationships of Arthropods to Precambrian and Cambrian Problematic Fossil Taxa". Systematic Biology 45 (2): 190–222. doi:10.2307/2413615. JSTOR 2413615.