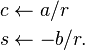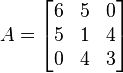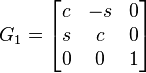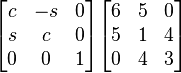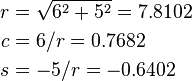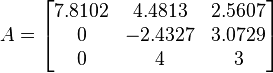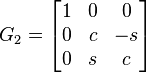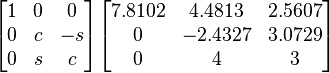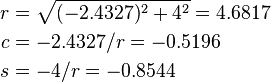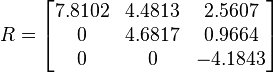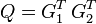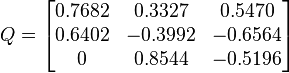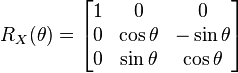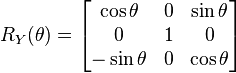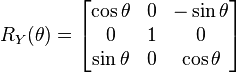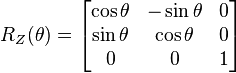Givens rotation

In numerical linear algebra, a Givens rotation is a rotation in the plane spanned by two coordinates axes. Givens rotations are named after Wallace Givens, who introduced them to numerical analysts in the 1950s while he was working at Argonne National Laboratory.

Matrix representation

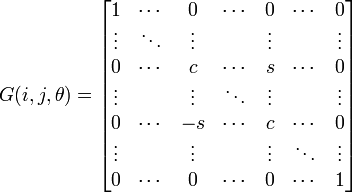
A Givens rotation is represented by a matrix of the form

G(i, j, \theta) = \begin{bmatrix} 1 & \cdots & 0 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & & \vdots & & \vdots \\ 0 & \cdots & c & \cdots & s & \cdots & 0 \\ \vdots & & \vdots & \ddots & \vdots & & \vdots \\ 0 & \cdots & -s & \cdots & c & \cdots & 0 \\ \vdots & & \vdots & & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & \cdots & 0 & \cdots & 1 \end{bmatrix}

where $c = cos θ$ and $s = sin θ$ appear at the intersections $i$ th and $j$ th rows and columns. That is, the non-zero elements of Givens matrix are given by:

\begin{align} g_{k\, k} &{}= 1 \qquad \text{for} \ k \ne i,\,j\\ g_{i\, i} &{}= c \\ g_{j\, j} &{}= c \\ g_{j\, i} &{}= -s \\ g_{i\, j} &{}= s \qquad \text{for} \ i > j \end{align}

(sign of sine switches for

j > i

)

The product $G (i, j, θ) x$ represents a counterclockwise rotation of the vector $x$ in the $(i, j)$ plane of $θ$ radians, hence the name Givens rotation.

The main use of Givens rotations in numerical linear algebra is to introduce zeros in vectors or matrices. This effect can, for example, be employed for computing the QR decomposition of a matrix. One advantage over Householder transformations is that they can easily be parallelised, and another is that often for very sparse matrices they have a lower operation count.

Stable calculation

When a Givens rotation matrix, $G (i, j, θ)$ , multiplies another matrix, $A$ , from the left, $G A$ , only rows $i$ and $j$ of $A$ are affected. Thus we restrict attention to the following problem. Given $a$ and $b$ , find $c = cos θ$ and $s = sin θ$ such that

\begin{bmatrix} c & -s \\ s & c \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} r \\ 0 \end{bmatrix} ,

where $r = \sqrt{a^2 + b^2}$ is the length of the vector $(a,b)$ . Explicit calculation of $θ$ is rarely necessary or desirable. Instead we directly seek $c$ and $s$ . An obvious solution would be

\begin{align} c &{}\larr a / r \\ s &{}\larr -b / r. \end{align}

However, the computation for $r$ may overflow or underflow. An alternative formulation avoiding this problem (Golub & Van Loan 1996, §5.1.8) is implemented as the hypot function in many programming languages .

Furthermore, as Anderson (2000) discovered in improving LAPACK, a previously overlooked numerical consideration is continuity. To achieve this, we require $r$ to be positive.

if (b = 0) then {c ← copysign(1,a); s ← 0; r ← abs(a)}
else if (a = 0) then {c ← 0; s ← -copysign(1,b); r ← abs(b)}
else if (abs(b) > abs(a)) then
  t ← a/b
  u ← copysign(sqrt(1+t*t),b)
  s ← -1/u
  c ← -s*t
  r ← b*u
else
  t ← b/a
  u ← copysign(sqrt(1+t*t),a)
  c ← 1/u
  s ← -c*t
  r ← a*u

This is written in terms of the IEEE 754 copysign(x,y) function, which provides a safe and cheap way to copy the sign of y to x. If that is not available, $| x | \cdot sgn(y)$ , using the abs and sgn functions, is an alternative.

Triangularization

Given the following 3×3 Matrix, perform two iterations of the Givens rotation to bring the matrix to an upper triangular matrix in order to compute the QR decomposition.

A = \begin{bmatrix} 6 & 5 & 0 \\ 5 & 1 & 4 \\ 0 & 4 & 3 \\ \end{bmatrix}

In order to form the desired matrix, we must zero elements (2,1) and (3,2). We first select element (2,1) to zero. Using a rotation matrix of:

G_{1} = \begin{bmatrix} c & -s & 0 \\ s & c & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}

We have the following matrix multiplication:

\begin{bmatrix} c & -s & 0 \\ s & c & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 6 & 5 & 0 \\ 5 & 1 & 4 \\ 0 & 4 & 3 \\ \end{bmatrix}

Where:

\begin{align} r &{}= \sqrt{6^2 + 5^2} = 7.8102 \\ c &{}= 6 / r = 0.7682\\ s &{}= -5 / r = -0.6402 \end{align}

Plugging in these values for $c$ and $s$ and performing the matrix multiplication above yields a new $A$ of:

A =\begin{bmatrix} 7.8102 & 4.4813 & 2.5607 \\ 0 & -2.4327 & 3.0729 \\ 0 & 4 & 3 \\ \end{bmatrix}

We now want to zero element (3,2) to finish off the process. Using the same idea as before, we have a rotation matrix of:

G_{2} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & c & -s \\ 0 & s & c \\ \end{bmatrix}

We are presented with the following matrix multiplication:

\begin{bmatrix} 1 & 0 & 0 \\ 0 & c & -s \\ 0 & s & c \\ \end{bmatrix} \begin{bmatrix} 7.8102 & 4.4813 & 2.5607 \\ 0 & -2.4327 & 3.0729 \\ 0 & 4 & 3 \\ \end{bmatrix}

Where:

\begin{align} r &{}= \sqrt{(-2.4327)^2 + 4^2} = 4.6817 \\ c &{}= -2.4327 / r = -0.5196 \\ s &{}= -4 / r = -0.8544 \end{align}

Plugging in these values for $c$ and $s$ and performing the multiplications gives us a new matrix of:

R = \begin{bmatrix} 7.8102 & 4.4813 & 2.5607 \\ 0 & 4.6817 & 0.9664 \\ 0 & 0 & -4.1843 \\ \end{bmatrix}

This new matrix R is the upper triangular matrix needed to perform an iteration of the QR decomposition. $Q$ is now formed using the transpose of the rotation matrices in the following manner:

Q = G_{1}^T\, G_{2}^T

Performing this matrix multiplication yields:

Q = \begin{bmatrix} 0.7682 & 0.3327 & 0.5470 \\ 0.6402 & -0.3992 & -0.6564 \\ 0 & 0.8544 & -0.5196 \\ \end{bmatrix}

This completes two iterations of the Givens Rotation and calculating the QR decomposition can now be done.

Givens rotations in Clifford Algebras

In Clifford algebras and its child structures like geometric algebra rotations are represented by bivectors. Givens rotations are represented by the external product of the basis vectors. Given any pair of basis vectors 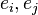$e_i, e_j$ Givens rotations bivectors are:

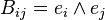
$B_{ij}=e_i\wedge e_j$

Their action on any vector is written:

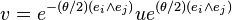
$v=e^{-(\theta/2)(e_i \wedge e_j)}u e^{(\theta/2)(e_i \wedge e_j)}$

where:

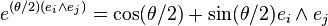
$e^{(\theta/2)(e_i \wedge e_j)}= \cos(\theta/2)+ \sin(\theta/2) e_i \wedge e_j$

Dimension 3

See also: Euler angles and Davenport rotations

There are three Givens rotations in dimension 3:

\begin{align} \\ R_X(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \end{bmatrix} \end{align}

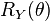Note: The $R_Y(\theta)$ matrix immediately below is not a Givens rotation. The 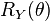$R_Y(\theta)$ matrix immediately below respects the right-hand rule ... and is this usual matrix one sees in Computer Graphics; however, a Givens rotation is simply a matrix as defined in the Matrix representation section above and does not necessarily respect the right-hand rule. This section should be considered suspect.

\begin{align} \\ R_Y(\theta) = \begin{bmatrix} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \end{bmatrix} \end{align}

Note: The actual Givens rotation matrix for 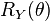$R_Y(\theta)$ would be:

\begin{align} \\ R_Y(\theta) = \begin{bmatrix} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \end{bmatrix} \end{align}

\begin{align} \\ R_Z(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{align}

Given that they are endomorphisms they can be composed with each other as many times as desired, keeping in mind that $g \circ f \neq f \circ g$ .

These three Givens rotations composed can generate any rotation matrix. This means that they can transform the standard basis of the space to any other frame in the space.

When rotations are performed in the right order, the values of the rotation angles of the final frame will be equal to the Euler angles of the final frame in the corresponding convention. For example, an operator 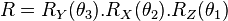$R = R_Y(\theta_3).R_X(\theta_2).R_Z(\theta_1)$ transforms the basis of the space into a frame with angles roll, pitch and yaw 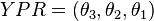$YPR = (\theta_3,\theta_2,\theta_1)$ in the Tait–Bryan convention z-x-y (convention in which the line of nodes is perpendicular to z and Y axes, also named Y-X′-Z″).

For the same reason, any rotation matrix in 3D can be decomposed in a product of three of these rotation operators.

The meaning of the composition of two Givens rotations $g \circ f$ is an operator that transforms vectors first by $f$ and then by $g$ , being $f$ and $g$ rotations about one axis of basis of the space. This is similar to the extrinsic rotation equivalence for Euler angles.

Table of composed rotations

The following table shows the three Givens rotations equivalent to the different Euler angles conventions using extrinsic composition (composition of rotations about the basis axes) of active rotations and the right-handed rule for the positive sign of the angles.

The notation has been simplified in such a way that $c 1$ means $cos θ 1$ and $s 2$ means $sin θ 2)$ . The subindexes of the angles are the order in which they are applied using extrinsic composition (1 for intrinsic rotation, 2 for nutation, 3 for precession)

As rotations are applied just in the opposite order of the Euler angles table of rotations, this table is the same but swapping indexes 1 and 3 in the angles associated with the corresponding entry. An entry like zxy means to apply first the y rotation, then x, and finally z, in the basis axes.

All the compositions assume the right hand convention for the matrices that are multiplied, yielding the following results.

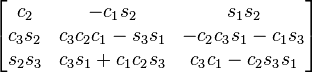
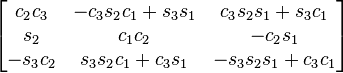
xzx	$\begin{bmatrix} c_2 & - c_1 s_2 & s_1 s_2 \\ c_3 s_2 & c_3 c_2 c_1 - s_3 s_1 & - c_2 c_3 s_1 - c_1 s_3 \\ s_2 s_3 & c_3 s_1 + c_1 c_2 s_3 & c_3 c_1 - c_2 s_3 s_1 \end{bmatrix}$	xzy	$\begin{bmatrix} c_2 c_3 & - c_3 s_2 c_1 + s_3 s_1 & c_3 s_2 s_1 + s_3 c_1 \\ s_2 & c_1 c_2 & - c_2 s_1 \\ - s_3 c_2 & s_3 s_2 c_1+c_3 s_1 & -s_3 s_2 s_1 + c_3 c_1 \end{bmatrix}$
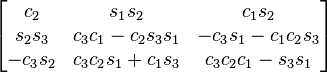
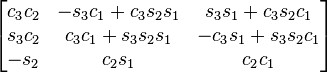
xyx	$\begin{bmatrix} c_2 & s_1 s_2 & c_1 s_2 \\ s_2 s_3 & c_3 c_1 - c_2 s_3 s_1 & - c_3 s_1 - c_1 c_2 s_3 \\ -c_3 s_2 & c_3 c_2 s_1 + c_1 s_3 & c_3 c_2 c_1 - s_3 s_1 \end{bmatrix}$	xyz	$\begin{bmatrix} c_3 c_2 & -s_3 c_1 + c_3 s_2 s_1 & s_3 s_1 + c_3 s_2 c_1 \\ s_3 c_2 & c_3 c_1 + s_3 s_2 s_1 & -c_3 s_1 + s_3 s_2 c_1 \\ -s_2 & c_2 s_1 & c_2 c_1 \end{bmatrix}$
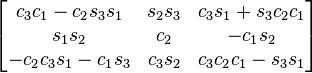
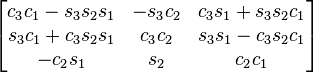
yxy	$\begin{bmatrix} c_3 c_1 - c_2 s_3 s_1 & s_2 s_3 & c_3 s_1 + s_3 c_2 c_1 \\ s_1 s_2 & c_2 & - c_1 s_2 \\ -c_2 c_3 s_1 - c_1 s_3 & c_3 s_2 & c_3 c_2 c_1 - s_3 s_1 \end{bmatrix}$	yxz	$\begin{bmatrix} c_3 c_1-s_3 s_2 s_1 & -s_3 c_2 & c_3 s_1+s_3 s_2 c_1 \\ s_3 c_1+c_3 s_2 s_1 & c_3 c_2 & s_3 s_1-c_3 s_2 c_1 \\ -c_2 s_1 & s_2 & c_2 c_1 \end{bmatrix}$
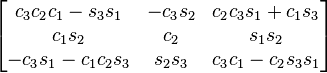
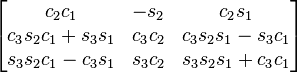
yxy	$\begin{bmatrix} c_3 c_2 c_1 - s_3 s_1 & - c_3 s_2 & c_2 c_3 s_1 + c_1 s_3 \\ c_1 s_2 & c_2 & s_1 s_2 \\ -c_3 s_1 - c_1 c_2 s_3 & s_2 s_3 & c_3 c_1 - c_2 s_3 s_1 \end{bmatrix}$	yzx	$\begin{bmatrix} c_2 c_1 & -s_2 & c_2 s_1 \\ c_3 s_2 c_1+s_3 s_1 & c_3 c_2 & c_3 s_2 s_1-s_3 c_1 \\ s_3 s_2 c_1-c_3 s_1 & s_3 c_2 & s_3 s_2 s_1+c_3 c_1 \end{bmatrix}$
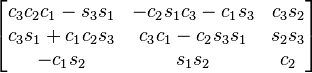
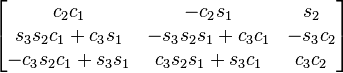
zyz	$\begin{bmatrix} c_3 c_2 c_1 - s_3 s_1 & - c_2 s_1 c_3 - c_1 s_3 & c_3 s_2 \\ c_3 s_1 + c_1 c_2 s_3 & c_3 c_1 - c_2 s_3 s_1 & s_2 s_3 \\ -c_1 s_2 & s_1 s_2 & c_2 \end{bmatrix}$	zyx	$\begin{bmatrix} c_2 c_1 & -c_2 s_1 & s_2 \\ s_3 s_2 c_1+c_3 s_1 & -s_3 s_2 s_1+c_3 c_1 & -s_3 c_2 \\ -c_3 s_2 c_1+s_3 s_1 & c_3 s_2 s_1+s_3 c_1 & c_3 c_2 \end{bmatrix}$
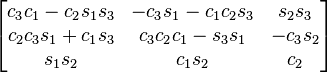
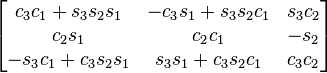
zxz	$\begin{bmatrix} c_3 c_1 - c_2 s_1 s_3 & - c_3 s_1 - c_1 c_2 s_3 & s_2 s_3 \\ c_2 c_3 s_1 + c_1 s_3 & c_3 c_2 c_1 - s_3 s_1 & - c_3 s_2 \\ s_1 s_2 & c_1 s_2 & c_2 \end{bmatrix}$	zxy	$\begin{bmatrix} c_3 c_1+s_3 s_2 s_1 & -c_3 s_1+s_3 s_2 c_1 & s_3 c_2 \\ c_2 s_1 & c_2 c_1 & -s_2 \\ -s_3 c_1+c_3 s_2 s_1 & s_3 s_1+c_3 s_2 c_1 & c_3 c_2 \end{bmatrix}$

References

Anderson, Edward (2000), Discontinuous Plane Rotations and the Symmetric Eigenvalue Problem . LAPACK Working Note 150, University of Tennessee, UT-CS-00-454, December 4, 2000.
Bindel, D.; Demmel, J.; Kahan, W.; Marques, O. (2000), On Computing Givens rotations reliably and efficiently . LAPACK Working Note 148, University of Tennessee, UT-CS-00-449, January 31, 2001.
Cybenko, George (March–April 2001), "Reducing Quantum Computations to Elementary Unitary Operations" (PDF), Computing in Science and Engineering 3 (2): 27–32, doi:10.1109/5992.908999
Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Johns Hopkins, ISBN 978-0-8018-5414-9 .
Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 11.3.1. Givens Method", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8

Numerical linear algebra

Key concepts	Floating point Numerical stability

Problems	Matrix multiplication (algorithms) Matrix decompositions Linear equations Sparse problems

Hardware	CPU cache TLB Cache-oblivious algorithm SIMD Multiprocessing

Software	BLAS Specialized libraries General purpose software

This article is issued from Wikipedia - version of the Friday, February 12, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.