Gibbs phenomenon
In mathematics, the Gibbs phenomenon, discovered by Henry Wilbraham (1848)[1] and rediscovered by J. Willard Gibbs (1899),[2] is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity. The nth partial sum of the Fourier series has large oscillations near the jump, which might increase the maximum of the partial sum above that of the function itself. The overshoot does not die out as n increases, but approaches a finite limit.[3] This sort of behavior was also observed by experimental physicists, but was believed to be due to imperfections in the measuring apparatuses.[4]
These are one cause of ringing artifacts in signal processing.
Description



The Gibbs phenomenon involves both the fact that Fourier sums overshoot at a jump discontinuity, and that this overshoot does not die out as more terms are added to the sum.
The three pictures on the right demonstrate the phenomenon for a square wave (of height  ) whose Fourier expansion is
) whose Fourier expansion is
More precisely, this is the function f which equals  between
between  and
and  and
and  between
between  and
and 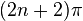 for every integer n; thus this square wave has a jump discontinuity of height
for every integer n; thus this square wave has a jump discontinuity of height  at every integer multiple of
at every integer multiple of 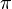 .
.
As can be seen, as the number of terms rises, the error of the approximation is reduced in width and energy, but converges to a fixed height. A calculation for the square wave (see Zygmund, chap. 8.5., or the computations at the end of this article) gives an explicit formula for the limit of the height of the error. It turns out that the Fourier series exceeds the height  of the square wave by
of the square wave by
or about 9 percent of the jump. More generally, at any jump point of a piecewise continuously differentiable function with a jump of a, the nth partial Fourier series will (for n very large) overshoot this jump by approximately  at one end and undershoot it by the same amount at the other end; thus the "jump" in the partial Fourier series will be about 18% larger than the jump in the original function. At the location of the discontinuity itself, the partial Fourier series will converge to the midpoint of the jump (regardless of what the actual value of the original function is at this point). The quantity
at one end and undershoot it by the same amount at the other end; thus the "jump" in the partial Fourier series will be about 18% larger than the jump in the original function. At the location of the discontinuity itself, the partial Fourier series will converge to the midpoint of the jump (regardless of what the actual value of the original function is at this point). The quantity
is sometimes known as the Wilbraham–Gibbs constant.
History
The Gibbs phenomenon was first noticed and analyzed by the obscure Henry Wilbraham.[1] He published a paper on it in 1848 that went unnoticed by the mathematical world.[5] Albert A. Michelson developed a device in 1898 that could compute and re-synthesize the Fourier series. A widespread myth says that when the Fourier coefficients for a square wave were input to the machine, the graph would oscillate at the discontinuities, and that because it was a physical device subject to manufacturing flaws, Michelson was convinced that the overshoot was caused by errors in the machine. In fact the graphs produced by the machine were not good enough to exhibit the Gibbs phenomenon clearly, and Michelson may not have noticed it as he made no mention of this effect in his paper (Michelson & Stratton 1898) about his machine or his later letters to Nature. Inspired by some correspondence in Nature between Michelson and Love about the convergence of the Fourier series of the square wave function, in 1898 J. Willard Gibbs published a short note in which he considered what today would be called a sawtooth wave and pointed out the important distinction between the limit of the graphs of the partial sums of the Fourier series, and the graph of the function that is the limit of those partial sums. In his first letter Gibbs failed to notice the Gibbs phenomenon, and the limit that he described for the graphs of the partial sums was inaccurate. In 1899 he published a correction in which he described the overshoot at the point of discontinuity (Nature: April 27, 1899, p. 606). In 1906, Maxime Bôcher gave a detailed mathematical analysis of that overshoot, which he called the "Gibbs phenomenon".[6]
Explanation
Informally, it reflects the difficulty inherent in approximating a discontinuous function by a finite series of continuous sine and cosine waves. It is important to put emphasis on the word finite because even though every partial sum of the Fourier series overshoots the function it is approximating, the limit of the partial sums does not. The value of x where the maximum overshoot is achieved moves closer and closer to the discontinuity as the number of terms summed increases so, again informally, once the overshoot has passed by a particular x, convergence at the value of x is possible.
There is no contradiction in the overshoot converging to a non-zero amount, but the limit of the partial sums having no overshoot, because the location of that overshoot moves. We have pointwise convergence, but not uniform convergence. For a piecewise C1 function the Fourier series converges to the function at every point except at the jump discontinuities. At the jump discontinuities themselves the limit will converge to the average of the values of the function on either side of the jump. This is a consequence of the Dirichlet theorem.[7]
The Gibbs phenomenon is also closely related to the principle that the decay of the Fourier coefficients of a function at infinity is controlled by the smoothness of that function; very smooth functions will have very rapidly decaying Fourier coefficients (resulting in the rapid convergence of the Fourier series), whereas discontinuous functions will have very slowly decaying Fourier coefficients (causing the Fourier series to converge very slowly). Note for instance that the Fourier coefficients 1, −1/3, 1/5, ... of the discontinuous square wave described above decay only as fast as the harmonic series, which is not absolutely convergent; indeed, the above Fourier series turns out to be only conditionally convergent for almost every value of x. This provides a partial explanation of the Gibbs phenomenon, since Fourier series with absolutely convergent Fourier coefficients would be uniformly convergent by the Weierstrass M-test and would thus be unable to exhibit the above oscillatory behavior. By the same token, it is impossible for a discontinuous function to have absolutely convergent Fourier coefficients, since the function would thus be the uniform limit of continuous functions and therefore be continuous, a contradiction. See more about absolute convergence of Fourier series.
Solutions
In practice, the difficulties associated with the Gibbs phenomenon can be ameliorated by using a smoother method of Fourier series summation, such as Fejér summation or Riesz summation, or by using sigma-approximation. Using a wavelet transform with Haar basis functions, the Gibbs phenomenon does not occur in the case of continuous data at jump discontinuities,[8] and is minimal in the discrete case at large change points. In wavelet analysis, this is commonly referred to as the Longo phenomenon.
Formal mathematical description of the phenomenon
Let  be a piecewise continuously differentiable function which is periodic with some period
be a piecewise continuously differentiable function which is periodic with some period  . Suppose that at some point
. Suppose that at some point 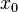 , the left limit
, the left limit 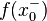 and right limit
and right limit 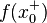 of the function
of the function  differ by a non-zero gap
differ by a non-zero gap  :
:
For each positive integer N ≥ 1, let SN f be the Nth partial Fourier series
where the Fourier coefficients  are given by the usual formulae
are given by the usual formulae
Then we have
and
but
More generally, if  is any sequence of real numbers which converges to
is any sequence of real numbers which converges to 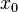 as
as  , and if the gap a is positive then
, and if the gap a is positive then
and
If instead the gap a is negative, one needs to interchange limit superior with limit inferior, and also interchange the ≤ and ≥ signs, in the above two inequalities.
Signal processing explanation
.svg.png)
From a signal processing point of view, the Gibbs phenomenon is the step response of a low-pass filter, and the oscillations are called ringing or ringing artifacts. Truncating the Fourier transform of a signal on the real line, or the Fourier series of a periodic signal (equivalently, a signal on the circle) corresponds to filtering out the higher frequencies by an ideal (brick-wall) low-pass/high-cut filter. This can be represented as convolution of the original signal with the impulse response of the filter (also known as the kernel), which is the sinc function. Thus the Gibbs phenomenon can be seen as the result of convolving a Heaviside step function (if periodicity is not required) or a square wave (if periodic) with a sinc function: the oscillations in the sinc function cause the ripples in the output.
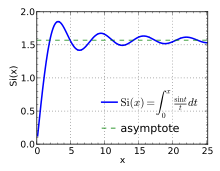
In the case of convolving with a Heaviside step function, the resulting function is exactly the integral of the sinc function, the sine integral; for a square wave the description is not as simply stated. For the step function, the magnitude of the undershoot is thus exactly the integral of the (left) tail, integrating to the first negative zero: for the normalized sinc of unit sampling period, this is  The overshoot is accordingly of the same magnitude: the integral of the right tail, or, which amounts to the same thing, the difference between the integral from negative infinity to the first positive zero, minus 1 (the non-overshooting value).
The overshoot is accordingly of the same magnitude: the integral of the right tail, or, which amounts to the same thing, the difference between the integral from negative infinity to the first positive zero, minus 1 (the non-overshooting value).
The overshoot and undershoot can be understood thus: kernels are generally normalized to have integral 1, so they result in a mapping of constant functions to constant functions – otherwise they have gain. The value of a convolution at a point is a linear combination of the input signal, with coefficients (weights) the values of the kernel. If a kernel is non-negative, such as for a Gaussian kernel, then the value of the filtered signal will be a convex combination of the input values (the coefficients (the kernel) integrate to 1, and are non-negative), and will thus fall between the minimum and maximum of the input signal – it will not undershoot or overshoot. If, on the other hand, the kernel assumes negative values, such as the sinc function, then the value of the filtered signal will instead be an affine combination of the input values, and may fall outside of the minimum and maximum of the input signal, resulting in undershoot and overshoot, as in the Gibbs phenomenon.
Taking a longer expansion – cutting at a higher frequency – corresponds in the frequency domain to widening the brick-wall, which in the time domain corresponds to narrowing the sinc function and increasing its height by the same factor, leaving the integrals between corresponding points unchanged. This is a general feature of the Fourier transform: widening in one domain corresponds to narrowing and increasing height in the other. This results in the oscillations in sinc being narrower and taller and, in the filtered function (after convolution), yields oscillations that are narrower and thus have less area, but does not reduce the magnitude: cutting off at any finite frequency results in a sinc function, however narrow, with the same tail integrals. This explains the persistence of the overshoot and undershoot.
-

Oscillations can be interpreted as convolution with a sinc.
-

Higher cutoff makes the sinc narrower but taller, with the same magnitude tail integrals, yielding higher frequency oscillations, but whose magnitude does not vanish.
Thus the features of the Gibbs phenomenon are interpreted as follows:
- the undershoot is due to the impulse response having a negative tail integral, which is possible because the function takes negative values;
- the overshoot offsets this, by symmetry (the overall integral does not change under filtering);
- the persistence of the oscillations is because increasing the cutoff narrows the impulse response, but does not reduce its integral – the oscillations thus move towards the discontinuity, but do not decrease in magnitude.
The square wave example

We now illustrate the above Gibbs phenomenon in the case of the square wave described earlier. In this case the period L is 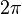 , the discontinuity
, the discontinuity 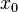 is at zero, and the jump a is equal to
is at zero, and the jump a is equal to  .
For simplicity let us just deal with the case when N is even (the case of odd N is very similar). Then
we have
.
For simplicity let us just deal with the case when N is even (the case of odd N is very similar). Then
we have
Substituting 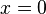 , we obtain
, we obtain
as claimed above. Next, we compute
If we introduce the normalized sinc function,  , we can rewrite this as
, we can rewrite this as
But the expression in square brackets is a numerical integration approximation to the integral 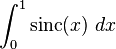 (more precisely, it is a midpoint rule approximation with spacing
(more precisely, it is a midpoint rule approximation with spacing  ). Since the sinc function is continuous, this approximation converges to the actual integral
as
). Since the sinc function is continuous, this approximation converges to the actual integral
as  . Thus we have
. Thus we have
which was what was claimed in the previous section. A similar computation shows
Consequences
In signal processing, the Gibbs phenomenon is undesirable because it causes artifacts, namely clipping from the overshoot and undershoot, and ringing artifacts from the oscillations. In the case of low-pass filtering, these can be reduced or eliminated by using different low-pass filters.
In MRI, the Gibbs phenomenon causes artifacts in the presence of adjacent regions of markedly differing signal intensity. This is most commonly encountered in spinal MR imaging, where the Gibbs phenomenon may simulate the appearance of syringomyelia.
See also
- σ-approximation which adjusts a Fourier summation to eliminate the Gibbs phenomenon which would otherwise occur at discontinuities
- Pinsky phenomenon
- Compare with Runge's phenomenon for polynomial approximations
- Sine integral
- Mach bands
Notes
- 1 2 Hewitt, Edwin; Hewitt, Robert E. (1979). "The Gibbs-Wilbraham phenomenon: An episode in Fourier analysis". Archive for History of Exact Sciences 21 (2): 129–160. doi:10.1007/BF00330404. Retrieved 16 September 2011. Available on-line at: National Chiao Tung University: Open Course Ware: Hewitt & Hewitt, 1979.
- ↑ Andrew Dimarogonas. Vibration for engineers. ISBN 0-13-462938-8.
- ↑ H. S. Carslaw (1930). Introduction to the theory of Fourier's series and integrals (Third ed.). New York: Dover Publications Inc. Chapter IX.
- ↑ Vretblad 2000 Section 4.7.
- ↑ Wilbraham, Henry (1848) "On a certain periodic function," The Cambridge and Dublin Mathematical Journal, 3 : 198-201.
- ↑ Bôcher, Maxime (April 1906) "Introduction to the theory of Fourier's series," Annals of Mathethematics, second series, 7 (3) : 81-152. The Gibbs phenomenon is discussed on pages 123-132; Gibbs' role is mentioned on page 129.
- ↑ M. Pinsky (2002). Introduction to Fourier Analysis and Wavelets. United states of America: Brooks/Cole. p. 27.
- ↑ Kelly, Susan E. "Gibbs Phenomenon for Wavelets." Applied and Computational Harmonic Analysis 3, 1995. http://www.uwlax.edu/faculty/kelly/Publications/GibbsJan.pdf
References
- Gibbs, J. Willard (1898), "Fourier's Series", Nature 59 (1522): 200, doi:10.1038/059200b0, ISSN 0028-0836
- Gibbs, J. Willard (1899), "Fourier's Series", Nature 59 (1539): 606, doi:10.1038/059606a0, ISSN 0028-0836
- Michelson, A. A.; Stratton, S. W. (1898), "A new harmonic analyser", Philosophical Magazine 5 (45): 85–91
- Antoni Zygmund, Trigonometrical series, Dover publications, 1955.
- Wilbraham, Henry (1848), "On a certain periodic function", The Cambridge and Dublin Mathematical Journal 3: 198–201
- Paul J. Nahin, Dr. Euler's Fabulous Formula, Princeton University Press, 2006. Ch. 4, Sect. 4.
- Vretblad, Anders (2000), Fourier Analysis and its Applications, Graduate Texts in Mathematics 223, New York: Springer Publishing, ISBN 0-387-00836-5
External links
- Hazewinkel, Michiel, ed. (2001), "Gibbs phenomenon", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W., "Gibbs Phenomenon". From MathWorld—A Wolfram Web Resource.
- Prandoni, Paolo, "Gibbs Phenomenon".
- Radaelli-Sanchez, Ricardo, and Richard Baraniuk, "Gibbs Phenomenon". The Connexions Project. (Creative Commons Attribution License)
- Horatio S Carslaw : Introduction to the theory of Fourier's series and integrals.pdf (introductiontot00unkngoog.pdf ) at archive.org
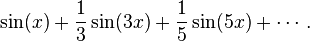





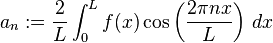
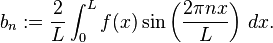
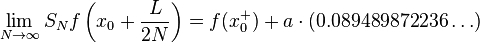







![S_N f\left(\frac{2\pi}{2N}\right) = \frac{\pi}{2} \left[ \frac{2}{N} \operatorname{sinc}\left(\frac{1}{N}\right) + \frac{2}{N} \operatorname{sinc}\left(\frac{3}{N}\right)
+ \cdots + \frac{2}{N} \operatorname{sinc}\left( \frac{(N-1)}{N} \right) \right].](../I/m/4049d55c356e2eefd0120dd6054ff91a.png)
![\begin{align}
\lim_{N \to \infty} S_N f\left(\frac{2\pi}{2N}\right)
& = \frac{\pi}{2} \int_0^1 \operatorname{sinc}(x)\, dx \\[8pt]
& = \frac{1}{2} \int_{x=0}^1 \frac{\sin(\pi x)}{\pi x}\, d(\pi x) \\[8pt]
& = \frac{1}{2} \int_0^\pi \frac{\sin(t)}{t}\ dt \quad = \quad \frac{\pi}{4} + \frac{\pi}{2} \cdot (0.089489872236\dots),
\end{align}](../I/m/e5668c719f9cccb56f512bd6e150572d.png)
