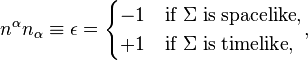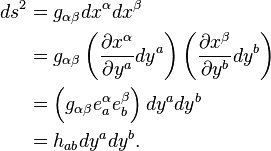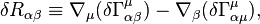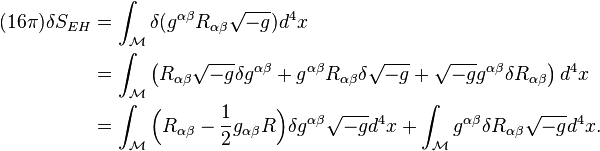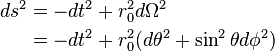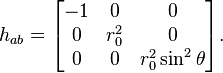Gibbons–Hawking–York boundary term
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.
The Einstein–Hilbert action is the basis for the most elementary variational principle from which the field equations of general relativity can be defined. However, the use of the Einstein–Hilbert action is appropriate only when the underlying spacetime manifold  is closed, i.e., a manifold which is both compact and without boundary. In the event that the manifold has a boundary
is closed, i.e., a manifold which is both compact and without boundary. In the event that the manifold has a boundary  , the action should be supplemented by a boundary term so that the variational principle is well-defined.
, the action should be supplemented by a boundary term so that the variational principle is well-defined.
The necessity of such a boundary term was first realised by York and later refined in a minor way by Gibbons and Hawking.
For a manifold that is not closed, the appropriate action is
where 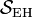 is the Einstein–Hilbert action,
is the Einstein–Hilbert action, 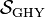 is the Gibbons–Hawking–York boundary term,
is the Gibbons–Hawking–York boundary term, 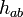 is the induced metric (see section below on definitions) on the boundary,
is the induced metric (see section below on definitions) on the boundary,  its determinant,
its determinant,  is the trace of the second fundamental form,
is the trace of the second fundamental form,  is equal to
is equal to 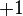 where
where  is timelike and
is timelike and 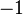 where
where  is spacelike, and
is spacelike, and 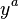 are the coordinates on the boundary. Varying the action with respect to the metric
are the coordinates on the boundary. Varying the action with respect to the metric 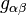 , subject to the condition
, subject to the condition

gives the Einstein equations; the addition of the boundary term means that in performing the variation, the geometry of the boundary encoded in the transverse metric 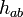 is fixed (see section below). There remains ambiguity in the action up to an arbitrary functional of the induced metric
is fixed (see section below). There remains ambiguity in the action up to an arbitrary functional of the induced metric 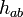 .
.
That a boundary term is needed in the gravitational case is due to the fact that  , the gravitational Lagrangian density, contains second derivatives of the metric tensor. This is a non-typical feature of field theories, which are usually formulated in terms of Lagrangians that involve first derivatives of fields to be varied over only.
, the gravitational Lagrangian density, contains second derivatives of the metric tensor. This is a non-typical feature of field theories, which are usually formulated in terms of Lagrangians that involve first derivatives of fields to be varied over only.
The GHY term is desirable, as it possesses a number of other key features. When passing to the hamiltonian formalism, it is necessary to include the GHY term in order to reproduce the correct Arnowitt-Deser-Misner energy (ADM energy). The term is required to ensure the path integral (a la Hawking) for quantum gravity has the correct composition properties. When calculating black hole entropy using the euclidean semiclassical approach, the entire contribution comes from the GHY term. This term has had more recent applications in loop quantum gravity in calculating transition amplitudes and background-independent scattering amplitudes.
In order to a finite value for the action, we may have to subtract off a surface term for flat spacetime:
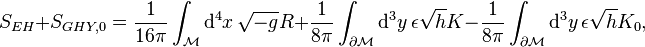
where  is the extrinsic curvature of the boundary imbedded flat spacetime. As
is the extrinsic curvature of the boundary imbedded flat spacetime. As 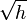 is invariant under variations of
is invariant under variations of 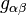 this addition term does not effect the field equations, as such this is referred to as the non-dynamical term.
this addition term does not effect the field equations, as such this is referred to as the non-dynamical term.
Introduction to hyper-surfaces
Defining hyper-surfaces
In a four-dimensional spacetime manifold, a hypersurface is a three-dimensional submanifold that can be either timelike, spacelike, or null.
A particular hyper-surface 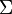 can be selected either by imposing a constraint on the coordinates
can be selected either by imposing a constraint on the coordinates
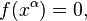
or by giving parametric equations,
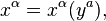
where 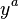 (
(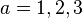 ) are coordinates intrinsic to the hyper-surface.
) are coordinates intrinsic to the hyper-surface.
For example, a two-sphere in three-dimensional Euclidean space can be described either by
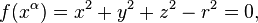
where  is the radius of the sphere, or by
is the radius of the sphere, or by

where  and
and  are intrinsic coordinates.
are intrinsic coordinates.
Hyper-surface orthogonal vector fields
We start with the family of hyper-surfaces given by
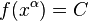
where different members of the family correspond to different values of the constant 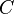 . Consider two neighbouring points
. Consider two neighbouring points  and
and 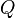 with coordinates
with coordinates 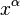 and
and 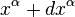 , respectively, lying in the same hyper-surface. We then have to first order
, respectively, lying in the same hyper-surface. We then have to first order
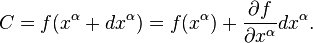
Subtracting off 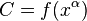 from this equation gives
from this equation gives
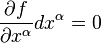
at  . This implies that
. This implies that 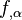 is normal to the hyper-surface. A unit normal
is normal to the hyper-surface. A unit normal 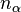 can be introduced in the case where the hyper-surface is not null. This is defined by
can be introduced in the case where the hyper-surface is not null. This is defined by
and we require that 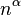 point in the direction of increasing
point in the direction of increasing 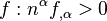 . It can then easily be checked that
. It can then easily be checked that 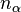 is given by
is given by

if the hyper-surface either spacelike or timelke.
Induced and transverse metric
The three vectors
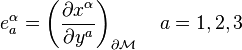
are tangential to the hyper-surface.
The induced metric is the three-tensor 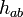 defined by
defined by

This acts as a metric tensor on the hyper-surface in the 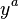 coordinates. For displacements confined to the hyper-surface (so that
coordinates. For displacements confined to the hyper-surface (so that  )
)
Because the three vectors 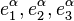 are tangential to the hyper-surface,
are tangential to the hyper-surface,
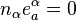
where 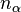 is the unit vector (
is the unit vector (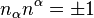 ) normal to the hyper-surface.
) normal to the hyper-surface.
We introduce what is called the transverse metric
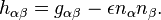
It isolates the part of the metric that is transverse to the normal 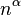 .
.
Is is easily seen that this four-tensor
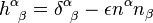
projects out the part of a four-vector transverse to the normal 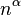 as
as

We have
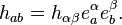
If we define 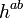 to be the inverse of
to be the inverse of 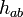 , it is easy to check
, it is easy to check
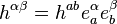
where

Note that variation subject to the condition

implies that 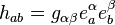 , the induced metric on
, the induced metric on  , is held fixed during the variation.
, is held fixed during the variation.
On Proving the main result
In the following subsections we will first compute the variation of the Einstein-Hilbert term and then the variation of the boundary term, and show that their sum results in

where 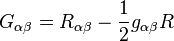 is the Einstein tensor, which produces the correct left-hand side to the Einstein field equations, without the cosmological term, which however is trivial to include by replacing
is the Einstein tensor, which produces the correct left-hand side to the Einstein field equations, without the cosmological term, which however is trivial to include by replacing 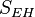 with
with

where 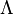 is the cosmological constant.
is the cosmological constant.
In the third subsection we elaborate on the meaning of the non-dynamical term.
Variation of the Einstein-Hilbert term
We will use the identity

and the Palatini identity:
which are both obtained in the article Einstein-Hilbert action.
We consider the variation of the Einstein-Hilbert term:
The first term gives us what we need for the left-hand side of the Einstein field equations. We must account for the second term.
By the Palatini identity
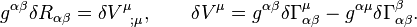
We will need Stokes theorem in the form:
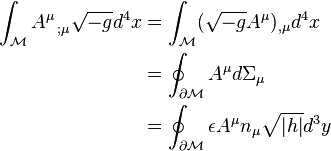
where  is the unit normal to
is the unit normal to 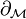 and
and  , and
, and 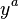 are coordinates on the boundary. And
are coordinates on the boundary. And 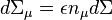 where
where  where
where ![h = \det [h_{ab}]](../I/m/11383aec66374e640c7ef3b08dea6ad7.png) , is an invariant three-dimensional volume element on the hyper-surface. In our particular case we take
, is an invariant three-dimensional volume element on the hyper-surface. In our particular case we take 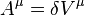 .
.
We now evaluate 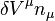 on the boundary
on the boundary  , keeping in mind that on
, keeping in mind that on  ,
, 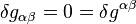 . Taking this into account we have
. Taking this into account we have

It is useful to note that

where in the second line we have swapped around  and
and 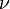 and used that the metric is symmetric. It is then not difficult to work out
and used that the metric is symmetric. It is then not difficult to work out 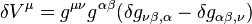 .
.
So now
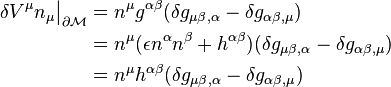
where in the second line we used the identity 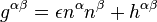 , and in the third line we have used the anti-symmetry in
, and in the third line we have used the anti-symmetry in  and
and  . As
. As  vanishes everywhere on the boundary,
vanishes everywhere on the boundary,  , its tangential derivatives must also vanish:
, its tangential derivatives must also vanish:  . It follows that
. It follows that 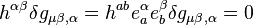 . So finally we have
. So finally we have
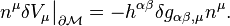
Gathering the results we obtain

We next show that the above boundary term will be cancelled by the variation of 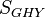 .
.
Variation of the boundary term
We now turn to the variation of the 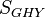 term. Because the induced metric is fixed on
term. Because the induced metric is fixed on  , the only quantity to be varied is
, the only quantity to be varied is  is the trace of the extrinsic curvature.
is the trace of the extrinsic curvature.
We have
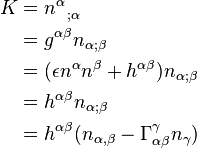
where we have used that 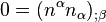 implies
implies 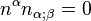 . So the variation of
. So the variation of  is
is
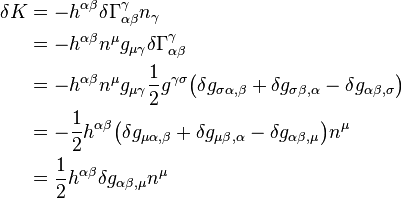
where we have use the fact that the tangential derivatives of  vanish on
vanish on  . We have obtained
. We have obtained
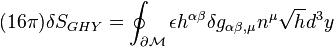
which cancels the second integral on the right-hand side of 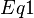 . The total variation of the gravitational action is:
. The total variation of the gravitational action is:
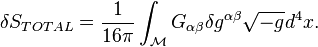
This produces the correct left-hand side of the Einstein equations. This proves the main result.
The non-dynamical term
We elaborate on the role of

in the gravitational action. As already mentioned above, because this term only depends on 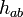 , its variation with respect to
, its variation with respect to 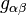 gives zero and so does not effect the field equations, its purpose is to change the numerical value of the action. As such we will refer to it as the non-dynamical term.
gives zero and so does not effect the field equations, its purpose is to change the numerical value of the action. As such we will refer to it as the non-dynamical term.
Let us assume that 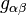 is a solution of the vacuum field equations, in which case the Ricci scalar
is a solution of the vacuum field equations, in which case the Ricci scalar  vanishes. The numerical value of the gravitational action is then
vanishes. The numerical value of the gravitational action is then
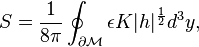
where we are ignoring the non-dynamical term for the moment. Let us evaluate this for flat spacetime. Choose the boundary  to consist of two hyper-surfaces of constant time value
to consist of two hyper-surfaces of constant time value 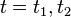 and a large three-cylinder at
and a large three-cylinder at 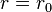 (that is, the product of a finite interval and a three-sphere of radius
(that is, the product of a finite interval and a three-sphere of radius  ). We have
). We have  on the hyper-surfaces of constant time. On the three cylinder, in coordinates intrinsic to the hyper-surface, the line element is
on the hyper-surfaces of constant time. On the three cylinder, in coordinates intrinsic to the hyper-surface, the line element is
meaning the induced metric is
so that  . The unit normal is
. The unit normal is 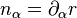 , so
, so 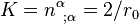 . Then
. Then

and diverges as 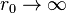 , that is, when the spatial boundary is pushed to infinity, even when the
, that is, when the spatial boundary is pushed to infinity, even when the 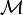 is bounded by two hyper-surfaces of constant time. One would expect the same problem for curved spacetimes that are asymptotically flat (there is no problem if the spacetime is compact). This problem is remedied by the non-dynamical term. The difference
is bounded by two hyper-surfaces of constant time. One would expect the same problem for curved spacetimes that are asymptotically flat (there is no problem if the spacetime is compact). This problem is remedied by the non-dynamical term. The difference 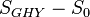 will be well defined in the limit
will be well defined in the limit 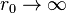 .
.
A path integral approach to quantum gravity
As mentioned at the beginning, the GHY term is required to ensure the path integral (a la Hawking et al) for quantum gravity has the correct composition properties.
This older approach to path-integral quantum gravity had a number of difficulties and unsolved problems. The starting point in this approach is Feynman's idea that one can represent the amplitude

to go from the state with metric  and matter fields
and matter fields  on a surface
on a surface  to a state with metric
to a state with metric  and matter fields
and matter fields  on a surface
on a surface 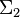 , as a sum over all field configurations
, as a sum over all field configurations  and
and  which take the boundary values of the fields on the surfaces
which take the boundary values of the fields on the surfaces  and
and 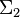 . We write
. We write
![<g_2 , \phi_2 , \Sigma_2 | g_1 , \phi_1 , \Sigma_1> = \int \mathcal{D} [g,\phi] \exp (i S [g,\phi])](../I/m/1b3fb7210ba78fdc51da92164dc67fce.png)
where ![\mathcal{D} [g,\phi]](../I/m/0ea0434abbc531ec0e341a065c0039b6.png) is a measure on the space of all field configurations
is a measure on the space of all field configurations  and
and  ,
, ![S [g,\phi]](../I/m/7b74f636c7219e97b1fb5b34680373f6.png) is the action of the fields, and the integral is taken over all fields which have the given values on
is the action of the fields, and the integral is taken over all fields which have the given values on  and
and 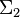 .
.
It is argued that one need only specify the three-dimensional induced metric  on the boundary.
on the boundary.
Now consider the situation where one makes the transition from metric  , on a surface
, on a surface  , to a metric
, to a metric 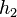 , on a surface
, on a surface 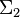 and then on to a metric
and then on to a metric 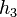 on a later surface
on a later surface 
One would like to have the usual composition rule
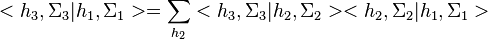
expressing that the amplitude to go from the initial to final state to be obtained by summing over all states on the intermediate surface 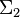 .
.
Let  be the metric between
be the metric between  and
and 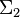 and
and  be the metric between
be the metric between 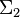 and
and  . Although the induced metric of
. Although the induced metric of  and
and  will agree on
will agree on 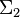 , the normal derivative of
, the normal derivative of  at
at 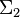 will not in general be equal to that of
will not in general be equal to that of  at
at 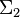 . Taking the implications of this into account, it can then be shown that the composition rule will hold if and only if we include the GHY boundary term.[1]
. Taking the implications of this into account, it can then be shown that the composition rule will hold if and only if we include the GHY boundary term.[1]
In the next section it is demonstrated how this path integral approach to quantum gravity leads to the concept of black hole temperature and intrinsic quantum mechanical entropy.
Calculating black hole entropy using the euclidean semiclassical approach
Application in loop quantum gravity
Transition amplitudes and the Hamilton's principal function
In the quantum theory, the object that corresponds to the Hamilton's principal function is the transition amplitude. Consider gravity defined on a compact region of spacetime, with the topology of a four dimensional ball. The boundary of this region is a three-dimensional space with the topology of a three-sphere, which we call 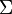 . In pure gravity without cosmological constant, since the Ricci scalar vanishes on solutions of Einstein's equations, the bulk action vanishes and the Hamilton's principal function is given entirely in terms of the boundary term,
. In pure gravity without cosmological constant, since the Ricci scalar vanishes on solutions of Einstein's equations, the bulk action vanishes and the Hamilton's principal function is given entirely in terms of the boundary term,
![S [q] = \int_\Sigma K^{ab} [q] q_{ab} \sqrt{q} \; d^3 \sigma](../I/m/f6a63eb2829622eb7dc92714d72ea2cb.png)
where 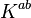 is the extrinsic curvature of the boundary,
is the extrinsic curvature of the boundary,  is the three-metric induced on the boundary, and
is the three-metric induced on the boundary, and 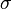 are coordinates on the boundary.
are coordinates on the boundary.
The functional ![S [q]](../I/m/2e30e83ef73fa1b7f23635f856b19c9c.png) is a highly non-trivial functional to compute; this is because the extrinsic curvature
is a highly non-trivial functional to compute; this is because the extrinsic curvature ![K^{ab} [q]](../I/m/de2ae28362da7fdeda19dd832b1ad652.png) is determined by the bulk solution singled out by the boundary intrinsic geometry. As such
is determined by the bulk solution singled out by the boundary intrinsic geometry. As such ![K^{ab} [q]](../I/m/de2ae28362da7fdeda19dd832b1ad652.png) is non-local. Knowing the general dependence of
is non-local. Knowing the general dependence of 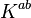 from
from  is equivalent to knowing the general solution of the Einstein equations.
is equivalent to knowing the general solution of the Einstein equations.
Background-independent scattering amplitudes
Loop quantum gravity is formulated in a background-independent language. No spacetime is assumed a priori, but rather it is built up by the states of theory themselves - however scattering amplitudes are derived from  -point functions (Correlation function (quantum field theory)) and these, formulated in conventional quantum field theory, are functions of points of a background space-time. The relation between the background-independent formalism and the conventional formalism of quantum field theory on a given spacetime is far from obvious, and it is far from obvious how to recover low-energy quantities from the full background-independent theory. One would like to derive the
-point functions (Correlation function (quantum field theory)) and these, formulated in conventional quantum field theory, are functions of points of a background space-time. The relation between the background-independent formalism and the conventional formalism of quantum field theory on a given spacetime is far from obvious, and it is far from obvious how to recover low-energy quantities from the full background-independent theory. One would like to derive the  -point functions of the theory from the background-independent formalism, in order to compare them with the standard perturbative expansion of quantum general relativity and therefore check that loop quantum gravity yields the correct low-energy limit.
-point functions of the theory from the background-independent formalism, in order to compare them with the standard perturbative expansion of quantum general relativity and therefore check that loop quantum gravity yields the correct low-energy limit.
A strategy for addressing this problem has been suggested;[2] the idea is to study the boundary amplitude, or transition amplitude of a compact region of spacetime, namely a path integral over a finite space-time region, seen as a function of the boundary value of the field.[3] In conventional quantum field theory, this boundary amplitude is well–defined[4][5] and codes the physical information of the theory; it does so in quantum gravity as well, but in a fully background–independent manner.[6] A generally covariant definition of  -point functions can then be based on the idea that the distance between physical points –arguments of the
-point functions can then be based on the idea that the distance between physical points –arguments of the  -point function is determined by the state of the gravitational field on the boundary of the spacetime region considered.
-point function is determined by the state of the gravitational field on the boundary of the spacetime region considered.
The key observation is that in gravity the boundary data include the gravitational field, hence the geometry of the boundary, hence all relevant relative distances and time separations. In other words, the boundary formulation realizes very elegantly in the quantum context the complete identification between spacetime geometry and dynamical fields.
References
- York, J. W. (1972). "Role of conformal three-geometry in the dynamics of gravitation". Physical Review Letters 28 (16): 1082. Bibcode:1972PhRvL..28.1082Y. doi:10.1103/PhysRevLett.28.1082.
- Gibbons, G. W.; Hawking, S. W. (1977). "Action integrals and partition functions in quantum gravity". Physical Review D 15 (10): 2752. Bibcode:1977PhRvD..15.2752G. doi:10.1103/PhysRevD.15.2752.
S. W. Hawking and G. T. Horowitz, ``The Gravitational Hamiltonian, action, entropy and surface terms," Class. Quant. Grav. 13 (1996) 1487 [arXiv:gr-qc/9501014].
J. D. Brown and J. W. . York, ``The Microcanonical functional integral. 1. The Gravitational field," Phys. Rev. D47, 1420 (1993) [arXiv:gr-qc/9209014].
| ||||||||||||||||||||||||||||
References
- ↑ For example see the book "Hawking on the big bang and black holes" by Stephen Hawking, chapter 15.
- ↑ L. Modesto, C. Rovelli:Particle scattering in loop quantum gravity, Phys Rev Lett 95 (2005) 191301
- ↑ R Oeckl, A ‘general boundary’ formulation for quantum mechanics and quantum gravity, Phys Lett B575 (2003) 318-324 ; Schrodinger's cat and the clock: lessons for quantum gravity, Class Quant Grav 20 (2003) 5371-5380l
- ↑ F. Conrady, C. Rovelli Generalized Schrodinger equation in Euclidean field theory", Int J Mod Phys A 19, (2004) 1-32.
- ↑ L Doplicher, Generalized Tomonaga-Schwinger equation from the Hadamard formula, Phys Rev D70 (2004) 064037
- ↑ F. Conrady, L. Doplicher, R. Oeckl, C. Rovelli, M. Testa, Minkowski vacuum in background independent quantum gravity, Phys Rev D69 (2004) 064019.