Giant component

In network theory, a giant component is a connected component of a given random graph that contains a constant fraction of the entire graph's vertices.

Giant components are a prominent feature of the Erdős–Rényi model of random graphs, in which each possible edge connecting pairs of a given set of $n$ vertices is present, independently of the other edges, with probability $p$ . In this model, if 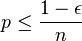$p \le \frac{1-\epsilon}{n}$ for any constant $\epsilon>0$ , then with high probability all connected components of the graph have size $O(log n)$ , and there is no giant component. 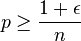However, for $p \ge \frac{1 + \epsilon}{n}$ there is with high probability a single giant component, with all other components having size $O(log n)$ . For 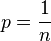$p = \frac{1}{n}$ , intermediate between these two possibilities, the number of vertices in the largest component of the graph is with high probability proportional to 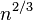$n^{2/3}$ .^[1]

Alternatively, if one adds randomly selected edges one at a time, starting with an empty graph, then it is not until approximately $n/2$ edges have been added that the graph contains a large component, and soon after that the component becomes giant. 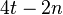More precisely, when $t$ edges have been added, for values of $t$ close to but larger than $n/2$ , the size of the giant component is approximately $4t-2n$ .^[1] However, according to the coupon collector's problem, $\Theta(n\log n)$ edges are needed in order to have high probability that the whole random graph is connected.

A similar sharp threshold between parameters that lead to graphs with all components small and parameters that lead to a giant component also occurs in random graphs with non-uniform degree distributions.^[2]

References

1 2 Bollobás, Béla (2001), "6. The Evolution of Random Graphs—The Giant Component", Random Graphs, Cambridge studies in advanced mathematics 73 (2nd ed.), Cambridge University Press, pp. 130–159, ISBN 978-0-521-79722-1 .
↑ Chung, Fan R. K.; Lu, Linyuan (2006), "6. The Rise of the Giant Component", Complex Graphs and Networks, Regional Conference Series in Mathematics 107, American Mathematical Society, pp. 113–142, ISBN 978-0-8218-3657-6 .

This article is issued from Wikipedia - version of the Wednesday, July 15, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.