Geometric and material buckling

In a nuclear reactor, criticality is achieved when the rate of neutron production is equal to the rate of neutron losses, including both neutron absorption and neutron leakage. Geometric buckling is a measure of neutron leakage, while material buckling is a measure of neutron production minus absorption. Thus, in the simplest case of a bare, homogeneous, steady state reactor, the geometric and material buckling must be equal.

Derivation

Both buckling terms are derived from the diffusion equation:^[1]

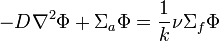$-D \nabla^2 \Phi + \Sigma_a \Phi = \frac{1}{k} \nu \Sigma_f \Phi$ .

where k is the criticality eigenvalue, 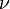$\nu$ is the neutrons per fission, 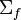$\Sigma_f$ is the macroscopic cross section for fission, and from diffusion theory, the diffusion coefficient is defined as:

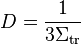$D=\frac{1}{3\Sigma_{\mathrm{tr}}}$ .

In addition, the diffusion length is defined as:

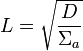$L=\sqrt{\frac{D}{\Sigma_a}}$ .

Rearranging the terms, the diffusion equation becomes:

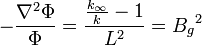$-\frac{\nabla^2 \Phi}{\Phi} = \frac{\frac{k_{\infty}}{k}-1}{L^2} = {B_g}^2$ .

The left side is the material buckling and the right side of the equation is the geometric buckling.

Geometric Buckling

The geometric buckling is an eigenvalue problem that can be solved for different geometries. The table below lists the geometric buckling for some common geometries.

Geometry	Geometric Buckling B_g²
Sphere of radius R	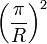$\left( \frac{\pi}{R} \right)^2$
Cylinder of height H and radius R	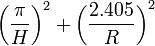$\left( \frac{\pi}{H} \right)^2 + \left( \frac{2.405}{R} \right)^2$
Parallelepiped with side lengths a, b and c	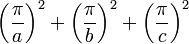$\left( \frac{\pi}{a} \right)^2 + \left( \frac{\pi}{b} \right)^2 + \left( \frac{\pi}{c} \right)^2$

Since the diffusion theory calculations overpredict the critical dimensions, an extrapolation distance δ must be subtracted to obtain an estimate of actual values. The buckling could also be calculated using actual dimensions and extrapolated distances using the following table.

Expressions for Geometric Buckling in Terms of Actual Dimensions and Extrapolated Distances.^[2]

Geometry	Geometric Buckling B_g²
Sphere of radius R	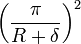$\left( \frac{\pi}{R+\delta} \right)^2$
Cylinder of height H and radius R	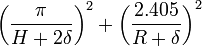$\left( \frac{\pi}{H+2\delta} \right)^2 + \left( \frac{2.405}{R+\delta} \right)^2$
Parallelepiped with side lengths a, b and c	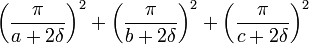$\left( \frac{\pi}{a+2\delta} \right)^2 + \left( \frac{\pi}{b+2\delta} \right)^2 + \left( \frac{\pi}{c+2\delta} \right)^2$

Material Buckling

Materials buckling is the buckling of a homogeneous configuration with respect to material properties only. If we redefine 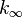$k_{\infty}$ in terms of purely material properties (and assume the fundamental mode), we have:

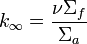$k_{\infty} = \frac{\nu \Sigma_f}{\Sigma_a}$ .

As stated previously, the geometric buckling is defined as:

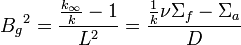${B_g}^2 = \frac{\frac{k_{\infty}}{k} - 1}{L^2} = \frac{\frac{1}{k} \nu \Sigma_f - \Sigma_a}{D}$ .

Solving for k (in the fundamental mode),

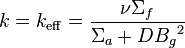$k = k_{\mathrm{eff}} = \frac{\nu \Sigma_f}{\Sigma_a + D {B_g}^2}$ ;

thus,

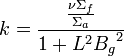$k = \frac{\frac{\nu \Sigma_f}{\Sigma_a}}{1 + L^2 {B_g}^2}$ .

Assuming the reactor is in a critical state (k = 1),

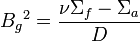${B_g}^2 = \frac{\nu \Sigma_f - \Sigma_a}{D}$ .

This expression is in purely material properties; therefore, this is called the materials buckling:

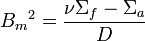${B_m}^2 = \frac{\nu \Sigma_f - \Sigma_a}{D}$ .

Critical Reactor Dimensions

By equating the geometric and material buckling, one can determine the critical dimensions of a one region nuclear reactor.

References

↑ Adams, Marvin L. (2009). Introduction to Nuclear Reactor Theory. Texas A&M University.
↑ Knief, Ronald A. (1985). Nuclear Criticality Safety: Theory and Practice (Softcover). American Nuclear Society. p. 236. ISBN 0-89448-028-6. Retrieved 15 May 2011.

This article is issued from Wikipedia - version of the Sunday, January 10, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.