Generalized gamma distribution
| Parameters |
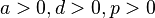 |
|---|---|
| Support |
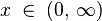 |
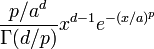 | |
| CDF |
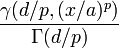 |
| Mean |
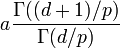 |
| Mode |
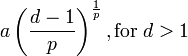 |
| Variance |
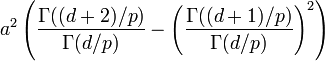 |
| Entropy |
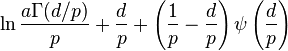 |
The generalized gamma distribution is a continuous probability distribution with three parameters. It is a generalization of the two-parameter gamma distribution. Since many distributions commonly used for parametric models in survival analysis (such as the Weibull distribution and the log-normal distribution) are special cases of the generalized gamma, it is sometimes used to determine which parametric model is appropriate for a given set of data.[1]
Characteristics
The generalized gamma has three parameters:  ,
, 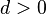 , and
, and 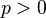 . For non-negative x, the probability density function of the generalized gamma is[2]
. For non-negative x, the probability density function of the generalized gamma is[2]
where 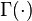 denotes the gamma function.
denotes the gamma function.
The cumulative distribution function is
where 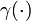 denotes the lower incomplete gamma function.
denotes the lower incomplete gamma function.
If 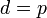 then the generalized gamma distribution becomes the Weibull distribution. Alternatively, if
then the generalized gamma distribution becomes the Weibull distribution. Alternatively, if  the generalised gamma becomes the gamma distribution.
the generalised gamma becomes the gamma distribution.
Alternative parameterisations of this distribution are sometimes used; for example with the substitution α = d/p.[3] In addition, a shift parameter can be added, so the domain of x starts at some value other than zero.[3] If the restrictions on the signs of a, d and p are also lifted (but α = d/p remains positive), this gives a distribution called the Amoroso distribution, after the Italian mathematician and economist Luigi Amoroso who described it in 1925.[4]
Moments
If X has a generalized gamma distribution as above, then[3]
Kullback-Leibler divergence
If 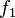 and
and 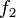 are the probability density functions of two generalized gamma distributions, then their Kullback-Leibler divergence is given by
are the probability density functions of two generalized gamma distributions, then their Kullback-Leibler divergence is given by
where 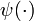 is the digamma function.[5]
is the digamma function.[5]
Software implementation
In R implemented in the package flexsurv, function dgengamma, with different parametrisation: 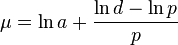 ,
, 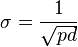 ,
, 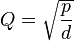 .
.
See also
References
- ↑ Box-Steffensmeier, Janet M.; Jones, Bradford S. (2004) Event History Modeling: A Guide for Social Scientists. Cambridge University Press. ISBN 0-521-54673-7 (pp. 41-43)
- ↑ Stacy, E.W. (1962). "A Generalization of the Gamma Distribution." Annals of Mathematical Statistics 33(3): 1187-1192. JSTOR 2237889
- 1 2 3 Johnson, N.L.; Kotz, S; Balakrishnan, N. (1994) Continuous Univariate Distributions, Volume 1, 2nd Edition. Wiley. ISBN 0-471-58495-9 (Section 17.8.7)
- ↑ Gavin E. Crooks (2010), The Amoroso Distribution, Technical Note, Lawrence Berkeley National Laboratory.
- ↑ C. Bauckhage (2014), Computing the Kullback-Leibler Divergence between two Generalized Gamma Distributions, arXiv:1401.6853.
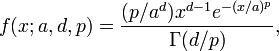
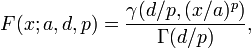
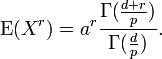
![\begin{align}
D_{KL} (f_1 \parallel f_2)
& = \int_{0}^{\infty} f_1(x; a_1, d_1, p_1) \, \ln \frac{f_1(x; a_1, d_1, p_1)}{f_2(x; a_2, d_2, p_2)} \, dx\\
& = \ln \frac{p_1 \, a_2^{d_2} \, \Gamma\left(d_2 / p_2\right)}{p_2 \, a_1^{d_1} \, \Gamma\left(d_1 /p_1\right)}
+ \left[ \frac{\psi\left( d_1 / p_1 \right)}{p_1} + \ln a_1 \right] (d_1 - d_2)
+ \frac{\Gamma\bigl((d_1+p_2) / p_1 \bigr)}{\Gamma\left(d_1 / p_1\right)} \left( \frac{a_1}{a_2} \right)^{p_2}
- \frac{d_1}{p_1}
\end{align}](../I/m/ab30c29869484f69f934be321bae54cc.png)