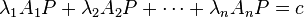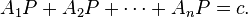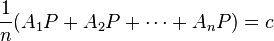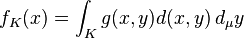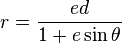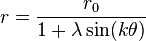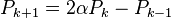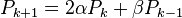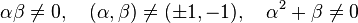Generalized conic
In mathematics, a generalized conic is a geometrical object defined by a property which is a generalization of some defining property of the classical conic. For example, in elementary geometry, an ellipse can be defined as the locus of a point which moves in a plane such that the sum of its distances from two fixed points in the plane is a constant. The curve obtained when the set of two fixed points is replaced by an arbitrary, but fixed, finite set of points in the plane can be thought of as a generalized ellipse. Since an ellipse is the equidistant set of two circles, the equidistant set of two arbitrary sets of points in a plane can be viewed as a generalized conic. In rectangular Cartesian coordinates, the equation y = x2 represents a parabola. The generalized equation y = xr, for r ≠ 0 and r ≠ 1, can be treated as defining a generalized parabola. The idea of generalized conic has found applications in approximation theory and optimization theory.[1]
Among the several possible ways in which the concept of a conic can be generalized, the most widely used approach is to define it as a generalization of the ellipse. The starting point for this approach is to look upon an ellipse as a curve satisfying the 'two-focus property': an ellipse is a curve that is the locus of points the sum of whose distances from two given points is constant. The two points are the foci of the ellipse. The curve obtained by replacing the set of two fixed points by an arbitrary, but fixed, finite set of points in the plane can be thought of as a generalized ellipse. Generalized conics with three foci are called trifocal ellipses. This can be further generalized to curves which are obtained as the loci of points which move such that the some of weighted arithmetic mean of the distances from a finite set of points is a constant. A still further generalization is possible by assuming that the weights attached to the distances can be of arbitrary sign, namely, plus or minus. Finally, the restriction that the set of fixed points, called the set of foci of the generalized conic, be finite may also be removed. The set may be assumed to be finite or infinite. In the infinite case, the weighted arithmetic mean has to be replaced by an appropriate integral. Generalized conics in this sense are also called polyellipses, egglipses, or, generalized ellipses. Since such curves were considered by the German mathematician Ehrenfried Walther von Tschirnhaus (1651 – 1708) they are also known as Tschirnhaus'sche Eikurve.[2] Also such generalizations have been discussed by Rene Descartes[3] and by James Clerk Maxwell.[4]
Multifocal oval curves
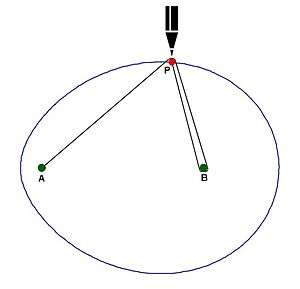

Rene Descartes (1596–1650), father of analytical geometry, in his La Geometrie published in 1637, set apart a section of about 15 pages to discuss what he had called bifocal ellipses. A bifocal oval was defined there as the locus of a point P which moves in a plane such that 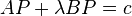 where A and B are fixed points in the plane and λ and c are constants which may be positive or negative. Descartes had introduced these ovals to determine the surfaces of glass such that after refraction the rays meet at the same point. Descartes had also recognized these ovals as generalizations of central conics, because for certain values of λ these ovals reduce to the familiar central conics, namely, the circle, the ellipse or the hyperbola.[3]
where A and B are fixed points in the plane and λ and c are constants which may be positive or negative. Descartes had introduced these ovals to determine the surfaces of glass such that after refraction the rays meet at the same point. Descartes had also recognized these ovals as generalizations of central conics, because for certain values of λ these ovals reduce to the familiar central conics, namely, the circle, the ellipse or the hyperbola.[3]
Multifocal ovals were rediscovered by James Clerk Maxwell (1831–1879) while he was still a school student. At the young age of 15, Maxwell wrote a scientific paper on these ovals with the title "Observations on circumscribed figures having a plurality of foci, and radii of various proportions" and got it presented by Professor J. D. Forbes in a meeting of the Royal Society of Edinburgh in 1846. Professor J. D. Forbes also published an account of the paper in the Proceedings of Royal Society of Edinburgh.[4][5] In his paper, though Maxwell did not use the term "generalized conic", he was considering curves defined by conditions which were generalizations of the defining condition of an ellipse.
Definition
A multifocal oval is a curve which is defined as the locus of a point moving such that
where A1, A2, . . . , An are fixed points in a plane and λ1, λ2, . . . , λn are fixed rational numbers and c is a constant. He gave simple pin-string-pencil methods for drawing such ovals.
The method for drawing the oval defined by the equation 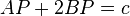 illustrates the general approach adopted by Maxwell for drawing such curves. Fix two pins at the foci A and B. Take a string whose length is c + AB and tie one end of the string to the pin at A. A pencil is attached to the other end of the string and the string is passed round the pin at the focus B. The pencil is then moved guided by the bight of the string. The curve traced by the pencil is the locus of P. His ingenuity is more visible in his description of the method for drawing a trifocal oval defined by an equation of the form
illustrates the general approach adopted by Maxwell for drawing such curves. Fix two pins at the foci A and B. Take a string whose length is c + AB and tie one end of the string to the pin at A. A pencil is attached to the other end of the string and the string is passed round the pin at the focus B. The pencil is then moved guided by the bight of the string. The curve traced by the pencil is the locus of P. His ingenuity is more visible in his description of the method for drawing a trifocal oval defined by an equation of the form 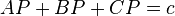 . Let three pins be fixed at the three foci A, B, C. Let one end of the string be fixed at the pin at C and let the string be passed around the other pins. Let the pencil be attached to the other end of the string. Let the pencil catch a bight in the string between A and C and then stretch to P. The pencil is moved such that the string is taut. The resulting figure would be a part of a trifocal ellipse. The positions of the string may have to adjusted to get the full oval.
. Let three pins be fixed at the three foci A, B, C. Let one end of the string be fixed at the pin at C and let the string be passed around the other pins. Let the pencil be attached to the other end of the string. Let the pencil catch a bight in the string between A and C and then stretch to P. The pencil is moved such that the string is taut. The resulting figure would be a part of a trifocal ellipse. The positions of the string may have to adjusted to get the full oval.
In the next two years since his paper was presented in the Royal Society of Edinburgh, Maxwell systematically developed the geometrical and optical properties of these ovals.[5]
Specialization and generalization of Maxwell's approach
As a special case of Maxwell's approach, consider the locus of a point which moves such that the following condition is satisfied:
Dividing by n and replacing c/n by c, this defining condition can be stated as
This suggests a simple interpretation: the generalised conic is a curve such that the average distance of every point P on the curve from the set {A1, A2, . . . , An} has the same constant value. This formulation of the concept of a generalized conic has been further generalised in several different ways.
- Change the definition of the average. In the formulation, the average was interpreted as the arithmetic mean. This may be replaced by other notions of averages like geometric mean of the distances. If the geometric mean is used to specify the average, the resulting curves turn out to be lemniscates. "Lemniscates are sets all of whose points have the same geometric mean of the distances (i.e. their product is constant). Lemniscates play a central role in the theory of approximation. The polynomial approximation of a holomorphic function can be interpreted as the approximation of the level curves with lemniscates. The product of distances corresponds to the absolute value of the root-decomposition of polynomials in the complex plane."[6]
- Change the cardinality of the focal set. Modify the definition so that the definition can be applied even in the case where the focal set infinite. This possibility was first introduced by C. Gross and T.-K. Strempel [2] and they posed the problem whether which results (of the classical case) can be extended to the case of infinitely many focal points or to continuous set of foci.[7]
- Change the dimension of the underlying space. The points may be assumed to lie in some d-dimensional space.
- Change the definition of the distance. Traditionally euclidean definitions are employed. in its place, other notions of distance like taxicab distance, may be used.[6][8] Generalized conics with this notion of distance have found applications in geometric tomography.[6][9]
The formulation of the definition of the generalized conic in the most general case when the cardinality of the focal set is infinite involves the notions of measurable sets and Lebesgue integration. All these have been employed by different authors and the resulting curves have been studied with special emphasis on applications.
Definition
Let 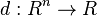 be a metric and
be a metric and  a measure on a compact set
a measure on a compact set 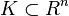 with
with 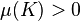 . The unweighted generalized conic function
. The unweighted generalized conic function 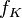 associated with
associated with  is
is
where 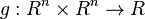 is a kernel function associated with
is a kernel function associated with 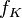 .
.  is the set of foci. The level sets
is the set of foci. The level sets 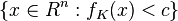 are called generalized conics.[6]
are called generalized conics.[6]
Generalized conics via polar equations


Given a conic, by choosing a focus of the conic as the pole and the line through the pole drawn parallel to the directrix of the conic as the polar axis, the polar equation of the conic can be written in the following form:
Here e is the eccentricity of the conic and d is the distance of the directrix from the pole. Tom M. Apostol and Mamikon A. Mnatsakanian in their study of curves drawn on the surfaces of right circular cones introduced a new class of curves which they called generalized conics.[10][11] These are curves whose polar equations are similar to the polar equations of ordinary conics and the ordinary conics appear as special cases of these generalized conics.
Definition
For constants r0 ≥ 0, λ ≥ 0 and real k, a plane curve described by the polar equation
is called a generalized conic.[11] The conic is called a generalized ellipse, parabola or hyperbola according as λ < 1, λ = 1, or λ > 1.
Special cases
- In the special case when k = 1, the generalized conic reduces to an ordinary conic.
- In the special case when k > 1, there is a simple geometrical method for the generation of the corresponding generalized conic.[11]
- Let α be an angle such that sin α = 1/k. Consider a right circular cone with semi-vertical angle equal to α. Consider the intersection of this cone by a plane such that the intersection is a conic with eccentricity λ. Unwrap the cone to a plane. Then the curve in the plane to which the conic section of eccentricity λ is unwrapped is a generalized conic with polar equation as specified in the definition.
- In the special case when k < 1, the generalized conic cannot be obtained by unwrapping a conic section. In this case there is another interpretation.
- Consider an ordinary conic drawn on a plane. Wrap the plane to form a right circular cone so that the conic becomes a curve in three-dimensional space. The projection of the curve onto a plane perpendicular to the axis of the cone will be a generalized conic in the sense of Apostol and Mnatsakanian with k < 1.
Examples
 r0 = 5, λ = 0.6, k = 1.5 |  r0 = 5, λ = 0.22, k = 5.5 |  r0 = 5, λ = 1, k = 1.5 | 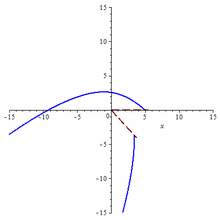 r0 = 5, λ = 1, k = 1.15 |
 r0 = 5, λ = 1.6, k = 1.5 |  r0 = 5, λ = 0.8, k = 0.5 |  r0 = 5, λ = 1.0, k = 0.5 |  r0 = 5, λ = 1.5, k = 0.5 |
Generalized conics in curve approximation
In 1996, Ruibin Qu introduced a new notion of generalized conic as a tool for generating approximations to curves.[12] The starting point for this generalization is the result that the sequence of points 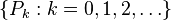 defined by
defined by
lie on a conic. In this approach, the generalized conic is now defined as below.
Definition
A generalized conic is such a curve that if the two points 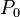 and
and 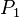 are on it, then the points
are on it, then the points 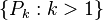 generated by the recursive relation
generated by the recursive relation
for some  and
and 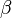 satisfying the relations
satisfying the relations
are also on it.
Generalized conics as equidistant sets

Definition
Let (X, d) be a metric space and let A be a nonempty subset of X. If x is a point in X, the distance of x from A is defined as d(x, A) = inf{ d(x, a): a in A}. If A and B are both nonempty subsets of X then the equidistant set determined by A and B is defined to be the set {x in X: d(x, A) = d(x, B)}. This equidistant set is denoted by { A = B }. The term generalized conic is used to denote a general equidistant set.[13]
Examples
Classical conics can be realized as equidistant sets. For example, if A is a singleton set and B is a straight line, then the equidistant set { A = B } is a parabola. If A and B are circles such that A is completely within B then the equidistant set { A = B } is an ellipse. On the other hand, if A lies completely outside B the equidistant set { A = B } is a hyperbola.
Further reading
- For a detailed discussion of generalized conics from the viewpoint of differential geometry, see the chapter on generalized conics in the book Convex Geometry by Csaba Vincze available online.[14]
References
- ↑ Csaba Vincze. "Convex Geometry". Retrieved 11 November 2015.
- ↑ Gyula Sz.-Nagy (June 1950). "Tschirnhaus'sche Eiflachen und EiKurven". Acta Mathematica Academiae Scientiarum Hungarica 1 (2): 167–181.
- 1 2 Ivor Grattan-Guinness (2005). Landmark Writings in Western Mathematics 1640–1940. Elsevier. p. 13. ISBN 9780080457444. Retrieved 15 December 2015.
- 1 2 James Clerk Maxwell (1990). The Scientific Letters and Papers of James Clerk Maxwell: 1846–1862 (Paper on the description of oval curves). CUP Archive. pp. 35–42. ISBN 9780521256254. Retrieved 11 November 2015.
- 1 2 P. M. Harman, Peter Michael Harman (February 2001). The Natural Philosophy of James Clerk Maxwell. Cambridge University Press. pp. 11–15. ISBN 9780521005852. Retrieved 15 December 2015.
- 1 2 3 4 Abris nagy (2015). "A short review on the theory of generalized conics" (PDF). Acta Mathematica Academiae Paedagogicae Nyiregyhaziensis 31: 81–96. Retrieved 17 December 2015.
- ↑ C. Gross and T.-K. Strempel (1998). "On generalizations of conics and on a generalization of the Fermat–Torricelli problem". American Mathematical Monthly 105 (8): 732–743.
- ↑ Akos G. Horvath, Horst Martini (2011). "Conics in Normed Planes" (PDF). Extracta Mathematicae 26 (1): 29–43. Retrieved 17 December 2015.
- ↑ Abris Nagy. "Generalized conics and geometric tomography" (PDF). Retrieved 17 December 2015.
- ↑ Tom M. Apostol and Mamikon A. Mnatsakanian (May 2007). "Unwrapping Curves from Cylinders and Cones" (PDF). American Mathematical Monthly 114: 388–416. Retrieved 11 December 2015.
- 1 2 3 Tom M. Apostol and Mamikon A. Mnatsakanian (2012). New Horizons in Geometry. The Maathematical Association of America. p. 197. ISBN 9780883853542.
- ↑ Ruibin Qu (December 1997). "Generalized conic curves and their applications in curve approximation". Approximation Theory and Its Applications 13 (4): 57–74.
- ↑ Mario Ponce, Patricio Santibánez (January 2014). "On equidistant sets and generalized conics: the old and the new" (PDF). The American Mathematical Monthly 121 ((1)): 18–32. Retrieved 10 November 2015.
- ↑ Csaba Vincze. "Convex Geometry Chapter 10. Generalized Conics". Digitalis Tankonyvtar. Retrieved 17 December 2015.