Generalized Appell polynomials
In mathematics, a polynomial sequence 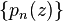 has a generalized Appell representation if the generating function for the polynomials takes on a certain form:
has a generalized Appell representation if the generating function for the polynomials takes on a certain form:
where the generating function or kernel  is composed of the series
is composed of the series
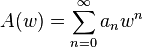 with
with 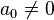
and
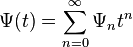 and all
and all 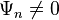
and
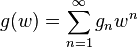 with
with 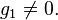
Given the above, it is not hard to show that  is a polynomial of degree
is a polynomial of degree  .
.
Boas–Buck polynomials are a slightly more general class of polynomials.
Special cases
- The choice of
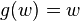 gives the class of Brenke polynomials.
gives the class of Brenke polynomials. - The choice of
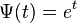 results in the Sheffer sequence of polynomials, which include the general difference polynomials, such as the Newton polynomials.
results in the Sheffer sequence of polynomials, which include the general difference polynomials, such as the Newton polynomials. - The combined choice of
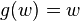 and
and 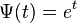 gives the Appell sequence of polynomials.
gives the Appell sequence of polynomials.
Explicit representation
The generalized Appell polynomials have the explicit representation
The constant is
where this sum extends over all partitions of  into
into 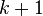 parts; that is, the sum extends over all
parts; that is, the sum extends over all 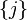 such that
such that
For the Appell polynomials, this becomes the formula
Recursion relation
Equivalently, a necessary and sufficient condition that the kernel  can be written as
can be written as 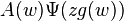 with
with 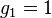 is that
is that
where 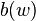 and
and 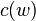 have the power series
have the power series
and
Substituting
immediately gives the recursion relation
For the special case of the Brenke polynomials, one has 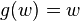 and thus all of the
and thus all of the 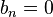 , simplifying the recursion relation significantly.
, simplifying the recursion relation significantly.
See also
References
- Ralph P. Boas, Jr. and R. Creighton Buck, Polynomial Expansions of Analytic Functions (Second Printing Corrected), (1964) Academic Press Inc., Publishers New York, Springer-Verlag, Berlin. Library of Congress Card Number 63-23263.
- William C. Brenke, On generating functions of polynomial systems, (1945) American Mathematical Monthly, 52 pp. 297–301.
- W. N. Huff, The type of the polynomials generated by f(xt) φ(t) (1947) Duke Mathematical Journal, 14 pp. 1091–1104.
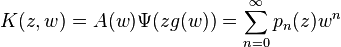
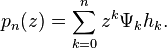
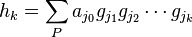
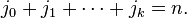
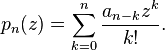
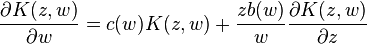
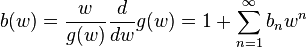
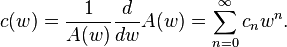
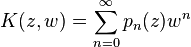
![z^{n+1} \frac {d}{dz} \left[ \frac{p_n(z)}{z^n} \right]=
-\sum_{k=0}^{n-1} c_{n-k-1} p_k(z)
-z \sum_{k=1}^{n-1} b_{n-k} \frac{d}{dz} p_k(z).](../I/m/931cb5f0130088bb0130cbbecef0b546.png)