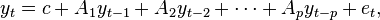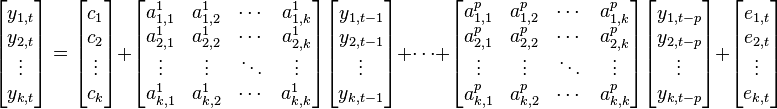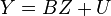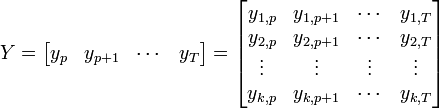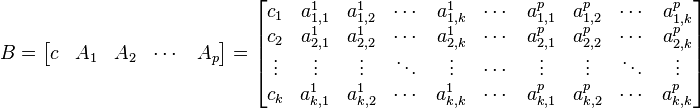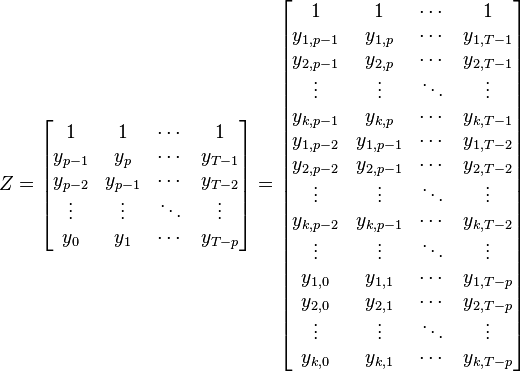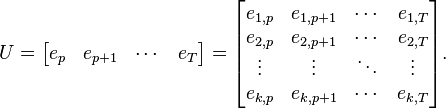General matrix notation of a VAR(p)
This page shows the details for different matrix notations of a vector autoregression process with k variables.
Var(p)
Main article: Vector autoregression
Where each  is a vector of length k and each
is a vector of length k and each  is a k × k matrix.
is a k × k matrix.
Large matrix notation
Equation by regression notation
Rewriting the y variables one to one gives:
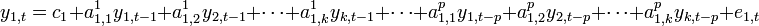
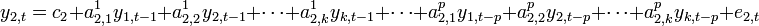
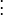
Concise matrix notation
One can rewrite a VAR(p) with k variables in a general way which includes T+1 observations  through
through 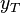
Where:
and
One can then solve for the coefficient matrix B (e.g. using an ordinary least squares estimation of 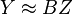 )
)
References
- Lütkepohl, Helmut (2005). New Introduction to Multiple Time Series Analysis. Berlin: Springer. ISBN 3540401725.
This article is issued from Wikipedia - version of the Monday, January 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.