g factor (psychometrics)

The g factor (also known as general intelligence, general mental ability or general intelligence factor) is a construct developed in psychometric investigations of cognitive abilities and human intelligence. It is a variable that summarizes positive correlations among different cognitive tasks, reflecting the fact that an individual's performance on one type of cognitive task tends to be comparable to that person's performance on other kinds of cognitive tasks. The g factor typically accounts for 40 to 50 percent of the between-individual performance differences on a given cognitive test, and composite scores ("IQ scores") based on many tests are frequently regarded as estimates of individuals' standing on the g factor.^[1] The terms general intelligence, general cognitive ability, general mental ability, or simply intelligence are often used interchangeably to refer to this common core shared by cognitive tests.^[2]

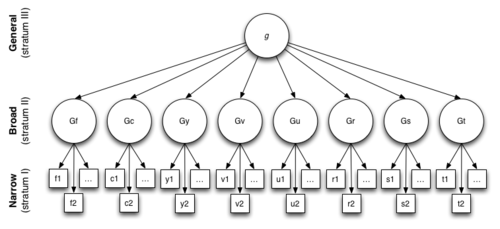
The existence of the g factor was originally proposed by the English psychologist Charles Spearman in the early years of the 20th century. He observed that children's performance ratings, across seemingly unrelated school subjects, were positively correlated, and reasoned that these correlations reflected the influence of an underlying general mental ability that entered into performance on all kinds of mental tests. Spearman suggested that all mental performance could be conceptualized in terms of a single general ability factor, which he labeled g, and a large number of narrow task-specific ability factors. Today's factor models of intelligence typically represent cognitive abilities as a three-level hierarchy, where there are a large number of narrow factors at the bottom of the hierarchy, a handful of broad, more general factors at the intermediate level, and at the apex a single factor, referred to as the g factor, which represents the variance common to all cognitive tasks.

Traditionally, research on g has concentrated on psychometric investigations of test data, with a special emphasis on factor analytic approaches. However, empirical research on the nature of g has also drawn upon experimental cognitive psychology and mental chronometry, brain anatomy and physiology, quantitative and molecular genetics, and primate evolution.^[3] While the existence of g as a statistical regularity is well-established and uncontroversial, there is no consensus as to what causes the positive correlations between tests.

Research in the field of behavioral genetics has established that the construct of g is highly heritable. It has a number of other biological correlates, including brain size. It is also a significant predictor of individual differences in many social outcomes, particularly in education and employment. The most widely accepted contemporary theories of intelligence incorporate the g factor.^[4] However, critics of g have contended that an emphasis on g is misplaced and entails a devaluation of other important abilities.

Cognitive ability testing

Cognitive ability tests are designed to measure different aspects of cognition. Specific domains assessed by tests include mathematical skill, verbal fluency, spatial visualization, and memory, among others. However, individuals who excel at one type of test tend to excel at other kinds of tests, too, while those who do poorly on one test tend to do so on all tests, regardless of the tests' contents.^[7] The English psychologist Charles Spearman was the first to describe this phenomenon.^[8] In a famous research paper published in 1904,^[9] he observed that children's performance measures across seemingly unrelated school subjects were positively correlated. This finding has since been replicated numerous times. The consistent finding of universally positive correlation matrices of mental test results (or the "positive manifold"), despite large differences in tests' contents, has been described as "arguably the most replicated result in all psychology."^[10] Zero or negative correlations between tests suggest the presence of sampling error or restriction of the range of ability in the sample studied.^[11]

Using factor analysis or related statistical methods, it is possible to compute a single common factor that can be regarded as a summary variable characterizing the correlations between all the different tests in a test battery. Spearman referred to this common factor as the general factor, or simply g. (By convention, g is always printed as a lower case italic.) Mathematically, the g factor is a source of variance among individuals, which entails that one cannot meaningfully speak of any one individual's mental abilities consisting of g or other factors to any specified degrees. One can only speak of an individual's standing on g (or other factors) compared to other individuals in a relevant population.^[11][12][13]

Different tests in a test battery may correlate with (or "load onto") the g factor of the battery to different degrees. These correlations are known as g loadings. An individual test taker's g factor score, representing his or her relative standing on the g factor in the total group of individuals, can be estimated using the g loadings. Full-scale IQ scores from a test battery will usually be highly correlated with g factor scores, and they are often regarded as estimates of g. For example, the correlations between g factor scores and full-scale IQ scores from David Wechsler's tests have been found to be greater than .95.^[1][11][14] The terms IQ, general intelligence, general cognitive ability, general mental ability, or simply intelligence are frequently used interchangeably to refer to the common core shared by cognitive tests.^[2]

The g loadings of mental tests are always positive and usually range between .10 and .90, with a mean of about .60 and a standard deviation of about .15. Raven's Progressive Matrices is among the tests with the highest g loadings, around .80. Tests of vocabulary and general information are also typically found to have high g loadings.^[15][16] However, the g loading of the same test may vary somewhat depending on the composition of the test battery.^[17]

The complexity of tests and the demands they place on mental manipulation are related to the tests' g loadings. For example, in the forward digit span test the subject is asked to repeat a sequence of digits in the order of their presentation after hearing them once at a rate of one digit per second. The backward digit span test is otherwise the same except that the subject is asked to repeat the digits in the reverse order to that in which they were presented. The backward digit span test is more complex than the forward digit span test, and it has a significantly higher g loading. Similarly, the g loadings of arithmetic computation, spelling, and word reading tests are lower than those of arithmetic problem solving, text composition, and reading comprehension tests, respectively.^[11][18]

Test difficulty and g loadings are distinct concepts that may or may not be empirically related in any specific situation. Tests that have the same difficulty level, as indexed by the proportion of test items that are failed by test takers, may exhibit a wide range of g loadings. For example, tests of rote memory have been shown to have the same level of difficulty but considerably lower g loadings than many tests that involve reasoning.^[18][19]

Theories

While the existence of g as a statistical regularity is well-established and uncontroversial among experts, there is no consensus as to what causes the positive intercorrelations. Several explanations have been proposed.^[20]

Mental energy or efficiency

Charles Spearman reasoned that correlations between tests reflected the influence of a common causal factor, a general mental ability that enters into performance on all kinds of mental tasks. However, he thought that the best indicators of g were those tests that reflected what he called the eduction of relations and correlates, which included abilities such as deduction, induction, problem solving, grasping relationships, inferring rules, and spotting differences and similarities. Spearman hypothesized that g was equivalent with "mental energy". However, this was more of a metaphorical explanation, and he remained agnostic about the physical basis of this energy, expecting that future research would uncover the exact physiological nature of g.^[21]

Following Spearman, Arthur Jensen maintained that all mental tasks tap into g to some degree. According to Jensen, the g factor represents a "distillate" of scores on different tests rather than a summation or an average of such scores, with factor analysis acting as the distillation procedure.^[16] He argued that g cannot be described in terms of the item characteristics or information content of tests, pointing out that very dissimilar mental tasks may have nearly equal g loadings. Wechsler similarly contended that g is not an ability at all but rather some general property of the brain. Jensen hypothesized that g corresponds to individual differences in the speed or efficiency of the neural processes associated with mental abilities.^[22] He also suggested that given the associations between g and elementary cognitive tasks, it should be possible to construct a ratio scale test of g that uses time as the unit of measurement.^[23]

Sampling theory

The so-called sampling theory of g, originally developed by E.L. Thorndike and Godfrey Thomson, proposes that the existence of the positive manifold can be explained without reference to a unitary underlying capacity. According to this theory, there are a number of uncorrelated mental processes, and all tests draw upon different samples of these processes. The intercorrelations between tests are caused by an overlap between processes tapped by the tests.^[24][25] Thus, the positive manifold arises due to a measurement problem, an inability to measure more fine-grained, presumably uncorrelated mental processes.^[13]

It has been shown that it is not possible to distinguish statistically between Spearman's model of g and the sampling model; both are equally able to account for intercorrelations among tests.^[26] The sampling theory is also consistent with the observation that more complex mental tasks have higher g loadings, because more complex tasks are expected to involve a larger sampling of neural elements and therefore have more of them in common with other tasks.^[27]

Some researchers have argued that the sampling model invalidates g as a psychological concept, because the model suggests that g factors derived from different test batteries simply reflect the shared elements of the particular tests contained in each battery rather than a g that is common to all tests. Similarly, high correlations between different batteries could be due to them measuring the same set of abilities rather than the same ability.^[28]

Critics have argued that the sampling theory is incongruent with certain empirical findings. Based on the sampling theory, one might expect that related cognitive tests share many elements and thus be highly correlated. However, some closely related tests, such as forward and backward digit span, are only modestly correlated, while some seemingly completely dissimilar tests, such as vocabulary tests and Raven's matrices, are consistently highly correlated. Another problematic finding is that brain damage frequently leads to specific cognitive impairments rather than a general impairment one might expect based on the sampling theory.^[13][29]

Mutualism

The "mutualism" model of g proposes that cognitive processes are initially uncorrelated, but that the positive manifold arises during individual development due to mutual beneficial relations between cognitive processes. Thus there is no single process or capacity underlying the positive correlations between tests. During the course of development, the theory holds, any one particularly efficient process will benefit other processes, with the result that the processes will end up being correlated with one another. Thus similarly high IQs in different persons may stem from quite different initial advantages that they had.^[13][30] Critics have argued that the observed correlations between the g loadings and the heritability coefficients of subtests are problematic for the mutualism theory.^[31]

Factor structure of cognitive abilities

An illustration of Spearman's two-factor intelligence theory. Each small oval is a hypothetical mental test. The blue areas correspond to test-specific variance (s), while the purple areas represent the variance attributed to g.

Factor analysis is a family of mathematical techniques that can be used to represent correlations between intelligence tests in terms of a smaller number of variables known as factors. The purpose is to simplify the correlation matrix by using hypothetical underlying factors to explain the patterns in it. When all correlations in a matrix are positive, as they are in the case of IQ, factor analysis will yield a general factor common to all tests. The general factor of IQ tests is referred to as the g factor, and it typically accounts for 40 to 50 percent of the variance in IQ test batteries.^[32]

Charles Spearman developed factor analysis in order to study correlations between tests. Initially, he developed a model of intelligence in which variations in all intelligence test scores are explained by only two kinds of variables: first, factors that are specific to each test (denoted s); and second, a g factor that accounts for the positive correlations across tests. This is known as Spearman's two-factor theory. Later research based on more diverse test batteries than those used by Spearman demonstrated that g alone could not account for all correlations between tests. Specifically, it was found that even after controlling for g, some tests were still correlated with each other. This led to the postulation of group factors that represent variance that groups of tests with similar task demands (e.g., verbal, spatial, or numerical) have in common in addition to the shared g variance.^[33]

An illustration of John B. Carroll's three stratum theory, an influential contemporary model of cognitive abilities. The broad abilities recognized by the model are fluid intelligence (Gf), crystallized intelligence (Gc), general memory and learning (Gy), broad visual perception (Gv), broad auditory perception (Gu), broad retrieval ability (Gr), broad cognitive speediness (Gs), and processing speed (Gt). Carroll regarded the broad abilities as different "flavors" of g.

Through factor rotation, it is, in principle, possible to produce an infinite number of different factor solutions that are mathematically equivalent in their ability to account for the intercorrelations among cognitive tests. These include solutions that do not contain a g factor. Thus factor analysis alone cannot establish what the underlying structure of intelligence is. In choosing between different factor solutions, researchers have to examine the results of factor analysis together with other information about the structure of cognitive abilities.^[34]

There are many psychologically relevant reasons for preferring factor solutions that contain a g factor. These include the existence of the positive manifold, the fact that certain kinds of tests (generally the more complex ones) have consistently larger g loadings, the substantial invariance of g factors across different test batteries, the impossibility of constructing test batteries that do not yield a g factor, and the widespread practical validity of g as a predictor of individual outcomes. The g factor, together with group factors, best represents the empirically established fact that, on average, overall ability differences between individuals are greater than differences among abilities within individuals, while a factor solution with orthogonal factors without g obscures this fact. Moreover, g appears to be the most heritable component of intelligence.^[35] Research utilizing the techniques of confirmatory factor analysis has also provided support for the existence of g.^[34]

A g factor can be computed from a correlation matrix of test results using several different methods. These include exploratory factor analysis, principal components analysis (PCA), and confirmatory factor analysis. Different factor-extraction methods produce highly consistent results, although PCA has sometimes been found to produce inflated estimates of the influence of g on test scores.^[17][36]

There is a broad contemporary consensus that cognitive variance between people can be conceptualized at three hierarchical levels, distinguished by their degree of generality. At the lowest, least general level there are a large number of narrow first-order factors; at a higher level, there are a relatively small number – somewhere between five and ten – of broad (i.e., more general) second-order factors (or group factors); and at the apex, there is a single third-order factor, g, the general factor common to all tests.^[37][38][39] The g factor usually accounts for the majority of the total common factor variance of IQ test batteries.^[40] Contemporary hierarchical models of intelligence include the three stratum theory and the Cattell–Horn–Carroll theory.^[41]

"Indifference of the indicator"

Spearman proposed the principle of the indifference of the indicator, according to which the precise content of intelligence tests is unimportant for the purposes of identifying g, because g enters into performance on all kinds of tests. Any test can therefore be used as an indicator of g. Following Spearman, Arthur Jensen more recently argued that a g factor extracted from one test battery will always be the same, within the limits of measurement error, as that extracted from another battery, provided that the batteries are large and diverse.^[42] According to this view, every mental test, no matter how distinctive, calls on g to some extent. Thus a composite score of a number of different tests will load onto g more strongly than any of the individual test scores, because the g components cumulate into the composite score, while the uncorrelated non-g components will cancel each other out. Theoretically, the composite score of an infinitely large, diverse test battery would, then, be a perfect measure of g.^[43]

In contrast, L.L. Thurstone argued that a g factor extracted from a test battery reflects the average of all the abilities called for by the particular battery, and that g therefore varies from one battery to another and "has no fundamental psychological significance."^[44] Along similar lines, John Horn argued that g factors are meaningless because they are not invariant across test batteries, maintaining that correlations between different ability measures arise because it is difficult to define a human action that depends on just one ability.^[45][46]

To show that different batteries reflect the same g, one must administer several test batteries to the same individuals, extract g factors from each battery, and show that the factors are highly correlated. This can be done within a confirmatory factor analysis framework.^[20] Wendy Johnson and colleagues have published two such studies.^[47][48] The first found that the correlations between g factors extracted from three different batteries were .99, .99, and 1.00, supporting the hypothesis that g factors from different batteries are the same and that the identification of g is not dependent on the specific abilities assessed. The second study found that g factors derived from four of five test batteries correlated at between .95–1.00, while the correlations ranged from .79 to .96 for the fifth battery, the Cattell Culture Fair Intelligence Test (the CFIT). They attributed the somewhat lower correlations with the CFIT battery to its lack of content diversity for it contains only matrix-type items, and interpreted the findings as supporting the contention that g factors derived from different test batteries are the same provided that the batteries are diverse enough. The results suggest that the same g can be consistently identified from different test batteries.^[37][49]

Population distribution

The form of the population distribution of g is unknown, because g cannot be measured on a ratio scale. (The distributions of scores on typical IQ tests are roughly normal, but this is achieved by construction, i.e., by normalizing the raw scores.) It has been argued that there are nevertheless good reasons for supposing that g is normally distributed in the general population, at least within a range of ±2 standard deviations from the mean. In particular, g can be thought of as a composite variable that reflects the additive effects of a large number of independent genetic and environmental influences, and such a variable should, according to the central limit theorem, follow a normal distribution.^[50]

Spearman's law of diminishing returns

A number of researchers have suggested that the proportion of variation accounted for by g may not be uniform across all subgroups within a population. Spearman's law of diminishing returns (SLDR), also termed the ability differentiation hypothesis, predicts that the positive correlations among different cognitive abilities are weaker among more intelligent subgroups of individuals. More specifically, SLDR predicts that the g factor will account for a smaller proportion of individual differences in cognitive tests scores at higher scores on the g factor.

SLDR was originally proposed by Charles Spearman,^[51] who reported that the average correlation between 12 cognitive ability tests was .466 in 78 normal children, and .782 in 22 "defective" children. Detterman and Daniel rediscovered this phenomenon in 1989.^[52] They reported that for subtests of both the WAIS and the WISC, subtest intercorrelations decreased monotonically with ability group, ranging from approximately an average intercorrelation of .7 among individuals with IQs less than 78 to .4 among individuals with IQs greater than 122.^[53]

SLDR has been replicated in a variety of child and adult samples who have been measured using broad arrays of cognitive tests. The most common approach has been to divide individuals into multiple ability groups using an observable proxy for their general intellectual ability, and then to either compare the average interrelation among the subtests across the different groups, or to compare the proportion of variation accounted for by a single common factor, in the different groups.^[54] However, as both Deary et al. (1996).^[54] and Tucker-Drob (2009)^[55] have pointed out, dividing the continuous distribution of intelligence into an arbitrary number of discrete ability groups is less than ideal for examining SLDR. Tucker-Drob (2009)^[55] extensively reviewed the literature on SLDR and the various methods by which it had been previously tested, and proposed that SLDR could be most appropriately captured by fitting a common factor model that allows the relations between the factor and its indicators to be nonlinear in nature. He applied such a factor model to a nationally representative data of children and adults in the United States and found consistent evidence for SLDR. For example, Tucker-Drob (2009) found that a general factor accounted for approximately 75% of the variation in seven different cognitive abilities among very low IQ adults, but only accounted for approximately 30% of the variation in the abilities among very high IQ adults.

Practical validity

The practical validity of g as a predictor of educational, economic, and social outcomes is more far-ranging and universal than that of any other known psychological variable. The validity of g is greater the greater the complexity of the task.^[56][57]

A test's practical validity is measured by its correlation with performance on some criterion external to the test, such as college grade-point average, or a rating of job performance. The correlation between test scores and a measure of some criterion is called the validity coefficient. One way to interpret a validity coefficient is to square it to obtain the variance accounted by the test. For example, a validity coefficient of .30 corresponds to 9 percent of variance explained. This approach has, however, been criticized as misleading and uninformative, and several alternatives have been proposed. One arguably more interpretable approach is to look at the percentage of test takers in each test score quintile who meet some agreed-upon standard of success. For example, if the correlation between test scores and performance is .30, the expectation is that 67 percent of those in the top quintile will be above-average performers, compared to 33 percent of those in the bottom quintile.^[58][59]

Academic achievement

The predictive validity of g is most conspicuous in the domain of scholastic performance. This is apparently because g is closely linked to the ability to learn novel material and understand concepts and meanings.^[56]

In elementary school, the correlation between IQ and grades and achievement scores is between .60 and .70. At more advanced educational levels, more students from the lower end of the IQ distribution drop out, which restricts the range of IQs and results in lower validity coefficients. In high school, college, and graduate school the validity coefficients are .50–.60, .40–.50, and .30–.40, respectively. The g loadings of IQ scores are high, but it is possible that some of the validity of IQ in predicting scholastic achievement is attributable to factors measured by IQ independent of g. According to research by Robert L. Thorndike, 80 to 90 percent of the predictable variance in scholastic performance is due to g, with the rest attributed to non-g factors measured by IQ and other tests.^[60]

Achievement test scores are more highly correlated with IQ than school grades. This may be because grades are more influenced by the teacher's idiosyncratic perceptions of the student.^[61] In a longitudinal English study, g scores measured at age 11 correlated with all the 25 subject tests of the national GCSE examination taken at age 16. The correlations ranged from .77 for the mathematics test to .42 for the art test. The correlation between g and a general educational factor computed from the GCSE tests was .81.^[62]

Research suggests that the SAT, widely used in college admissions, is primarily a measure of g. A correlation of .82 has been found between g scores computed from an IQ test battery and SAT scores. In a study of 165,000 students at 41 U.S. colleges, SAT scores were found to be correlated at .47 with first-year college grade-point average after correcting for range restriction in SAT scores (the correlation rises to .55 when course difficulty is held constant, i.e., if all students attended the same set of classes).^[58][63]

Job attainment

There is a high correlation of .90 to .95 between the prestige rankings of occupations, as rated by the general population, and the average general intelligence scores of people employed in each occupation. At the level of individual employees, the association between job prestige and g is lower – one large U.S. study reported a correlation of .65 (.72 corrected for attenuation). Mean level of g thus increases with perceived job prestige. It has also been found that the dispersion of general intelligence scores is smaller in more prestigious occupations than in lower level occupations, suggesting that higher level occupations have minimum g requirements.^[64][65]

Job performance

Research indicates that tests of g are the best single predictors of job performance, with an average validity coefficient of .55 across several meta-analyses of studies based on supervisor ratings and job samples. The average meta-analytic validity coefficient for performance in job training is .63.^[66] The validity of g in the highest complexity jobs (professional, scientific, and upper management jobs) has been found to be greater than in the lowest complexity jobs, but g has predictive validity even for the simplest jobs. Research also shows that specific aptitude tests tailored for each job provide little or no increase in predictive validity over tests of general intelligence. It is believed that g affects job performance mainly by facilitating the acquisition of job-related knowledge. The predictive validity of g is greater than that of work experience, and increased experience on the job does not decrease the validity of g.^[56][64]

Income

The correlation between income and g, as measured by IQ scores, averages about .40 across studies. The correlation is higher at higher levels of education and it increases with age, stabilizing when people reach their highest career potential in middle age. Even when education, occupation and socioeconomic background are held constant, the correlation does not vanish.^[67]

Other correlates

The g factor is reflected in many social outcomes. Many social behavior problems, such as dropping out of school, chronic welfare dependency, accident proneness, and crime, are negatively correlated with g independent of social class of origin.^[68] Health and mortality outcomes are also linked to g, with higher childhood test scores predicting better health and mortality outcomes in adulthood (see Cognitive epidemiology).^[69]

Genetic and environmental determinants

Heritability is the proportion of phenotypic variance in a trait in a population that can be attributed to genetic factors. The heritability of g has been estimated to fall between 40 to 80 percent using twin, adoption, and other family study designs as well as molecular genetic methods. It has been found to increase linearly with age. For example, a large study involving more than 11,000 pairs of twins from four countries reported the heritability of g to be 41 percent at age nine, 55 percent at age twelve, and 66 percent at age seventeen. Other studies have estimated that the heritability is as high as 80 percent in adulthood, although it may decline in old age. Most of the research on the heritability of g has been conducted in the USA and Western Europe, but studies in Russia (Moscow), the former East Germany, Japan, and rural India have yielded similar estimates of heritability as Western studies.^{[37][70][71][72]}

Behavioral genetic research has also established that the shared (or between-family) environmental effects on g are strong in childhood, but decline thereafter and are negligible in adulthood. This indicates that the environmental effects that are important to the development of g are unique and not shared between members of the same family.^[71]

The genetic correlation is a statistic that indicates the extent to which the same genetic effects influence two different traits. If the genetic correlation between two traits is zero, the genetic effects on them are independent, whereas a correlation of 1.0 means that the same set of genes explains the heritability of both traits (regardless of how high or low the heritability of each is). Genetic correlations between specific mental abilities (such as verbal ability and spatial ability) have been consistently found to be very high, close to 1.0. This indicates that genetic variation in cognitive abilities is almost entirely due to genetic variation in whatever g is. It also suggests that what is common among cognitive abilities is largely caused by genes, and that independence among abilities is largely due to environmental effects. Thus it has been argued that when genes for intelligence are identified, they will be "generalist genes", each affecting many different cognitive abilities.^[71][73][74]

The g loadings of mental tests have been found to correlate with their heritabilities, with correlations ranging from moderate to perfect in various studies. Thus the heritability of a mental test is usually higher the larger its g loading is.^[31]

Much research points to g being a highly polygenic trait influenced by a large number of common genetic variants, each having only small effects. Another possibility is that heritable differences in g are due to individuals having different "loads" of rare, deleterious mutations, with genetic variation among individuals persisting due to mutation–selection balance.^[74][75]

A number of candidate genes have been reported to be associated with intelligence differences, but the effect sizes have been small and almost none of the findings have been replicated. No individual genetic variants have been conclusively linked to intelligence in the normal range so far. Many researchers believe that very large samples will be needed to reliably detect individual genetic polymorphisms associated with g.^[37][75] However, while genes influencing variation in g in the normal range have proven difficult to find, a large number of single-gene disorders with mental retardation among their symptoms have been discovered.^[76]

Several studies suggest that tests with larger g loadings are more affected by inbreeding depression lowering test scores. There is also evidence that tests with larger g loadings are associated with larger positive heterotic effects on test scores. Inbreeding depression and heterosis suggest the presence of genetic dominance effects for g.^[77]

Neuroscientific findings

g has a number of correlates in the brain. Studies using magnetic resonance imaging (MRI) have established that g and total brain volume are moderately correlated (r~.3–.4). External head size has a correlation of ~.2 with g. MRI research on brain regions indicates that the volumes of frontal, parietal and temporal cortices, and the hippocampus are also correlated with g, generally at .25 or more, while the correlations, averaged over many studies, with overall grey matter and overall white matter have been found to be .31 and .27, respectively. Some but not all studies have also found positive correlations between g and cortical thickness. However, the underlying reasons for these associations between the quantity of brain tissue and differences in cognitive abilities remain largely unknown.^[2]

Most researchers believe that intelligence cannot be localized to a single brain region, such as the frontal lobe. Brain lesion studies have found small but consistent associations indicating that people with more white matter lesions tend to have lower cognitive ability. Research utilizing NMR spectroscopy has discovered somewhat inconsistent but generally positive correlations between intelligence and white matter integrity, supporting the notion that white matter is important for intelligence.^[2]

Some research suggests that aside from the integrity of white matter, also its organizational efficiency is related to intelligence. The hypothesis that brain efficiency has a role in intelligence is supported by functional MRI research showing that more intelligent people generally process information more efficiently, i.e., they use fewer brain resources for the same task than less intelligent people.^[2]

Small but relatively consistent associations with intelligence test scores include also brain activity, as measured by EEG records or event-related potentials, and nerve conduction velocity.^[78][79]

g in non-humans

Evidence of a general factor of intelligence has also been observed in non-human animals. Studies have shown that g is responsible for 47% of the individual variance in primates^[80] and between 55% and 60% in mice.^[81][82] While not able to be assessed using the same intelligence measures used in humans, cognitive ability can be measured with a variety of interactive and observational tools focusing on innovation, habit reversal, social learning, and responses to novelty.

Non-human models of g such as mice are used to study genetic influences on intelligence and neurological developmental research into the mechanisms behind and biological correlates of g.^[83]

Other biological associations

Height is correlated with intelligence (r~.2), but this correlation has not generally been found within families (i.e., among siblings), suggesting that it results from cross-assortative mating for height and intelligence. Myopia is known to be associated with intelligence, with a correlation of around .2 to .25, and this association has been found within families, too.^[84]

Group similarities and differences

Cross-cultural studies indicate that the g factor can be observed whenever a battery of diverse, complex cognitive tests is administered to a human sample. The factor structure of IQ tests has also been found to be consistent across sexes and ethnic groups in the U.S. and elsewhere.^[79] The g factor has been found to be the most invariant of all factors in cross-cultural comparisons. For example, when the g factors computed from an American standardization sample of Wechsler's IQ battery and from large samples who completed the Japanese translation of the same battery were compared, the congruence coefficient was .99, indicating virtual identity. Similarly, the congruence coefficient between the g factors obtained from white and black standardization samples of the WISC battery in the U.S. was .995, and the variance in test scores accounted for by g was highly similar for both groups.^[85]

Most studies suggest that there are negligible differences in the mean level of g between the sexes, and that sex differences in cognitive abilities are to be found in more narrow domains. For example, males generally outperform females in spatial tasks, while females generally outperform males in verbal tasks. Another difference that has been found in many studies is that males show more variability in both general and specific abilities than females, with proportionately more males at both the low end and the high end of the test score distribution.^[86]

Consistent differences between racial and ethnic groups in g have been found, particularly in the U.S. A 2001 meta-analysis of millions of subjects indicated that there is a 1.1 standard deviation gap in the mean level of g between white and black Americans, favoring the former. The mean score of Hispanic Americans was found to be .72 standard deviations below that of non-Hispanic whites.^[87] In contrast, Americans of East Asian descent generally slightly outscore white Americans.^[88] Several researchers have suggested that the magnitude of the black-white gap in cognitive ability tests is dependent on the magnitude of the test's g loading, with tests showing higher g loadings producing larger gaps (see Spearman's hypothesis).^[89] It has also been claimed that racial and ethnic differences similar to those found in the U.S. can be observed globally.^[90]

Relation to other psychological constructs

Elementary cognitive tasks

An illustration of the Jensen box, an apparatus for measuring choice reaction time.

Elementary cognitive tasks (ECTs) also correlate strongly with g. ECTs are, as the name suggests, simple tasks that apparently require very little intelligence, but still correlate strongly with more exhaustive intelligence tests. Determining whether a light is red or blue and determining whether there are four or five squares drawn on a computer screen are two examples of ECTs. The answers to such questions are usually provided by quickly pressing buttons. Often, in addition to buttons for the two options provided, a third button is held down from the start of the test. When the stimulus is given to the subject, they remove their hand from the starting button to the button of the correct answer. This allows the examiner to determine how much time was spent thinking about the answer to the question (reaction time, usually measured in small fractions of second), and how much time was spent on physical hand movement to the correct button (movement time). Reaction time correlates strongly with g, while movement time correlates less strongly.^[91] ECT testing has allowed quantitative examination of hypotheses concerning test bias, subject motivation, and group differences. By virtue of their simplicity, ECTs provide a link between classical IQ testing and biological inquiries such as fMRI studies.

Working memory

One theory holds that g is identical or nearly identical to working memory capacity. Among other evidence for this view, some studies have found factors representing g and working memory to be perfectly correlated. However, in a meta-analysis the correlation was found to be considerably lower.^[92] One criticism that has been made of studies that identify g with working memory is that "we do not advance understanding by showing that one mysterious concept is linked to another."^[93]

Piagetian tasks

Psychometric theories of intelligence aim at quantifying intellectual growth and identifying ability differences between individuals and groups. In contrast, Jean Piaget's theory of cognitive development seeks to understand qualitative changes in children's intellectual development. Piaget designed a number of tasks to verify hypotheses arising from his theory. The tasks were not intended to measure individual differences, and they have no equivalent in psychometric intelligence tests.^[94][95] For example, in one of the best-known Piagetian conservation tasks a child is asked if the amount of water in two identical glasses is the same. After the child agrees that the amount is the same, the investigator pours the water from one of the glasses into a glass of different shape so that the amount appears different although it remains the same. The child is then asked if the amount of water in the two glasses is the same or different.

Notwithstanding the different research traditions in which psychometric tests and Piagetian tasks were developed, the correlations between the two types of measures have been found to be consistently positive and generally moderate in magnitude. A common general factor underlies them. It has been shown that it is possible to construct a battery consisting of Piagetian tasks that is as good a measure of g as standard IQ tests.^[94][96]

Personality

The traditional view in psychology is that there is no meaningful relationship between personality and intelligence, and that the two should be studied separately. Intelligence can be understood in terms of what an individual can do, or what his or her maximal performance is, while personality can be thought of in terms of what an individual will typically do, or what his or her general tendencies of behavior are. Research has indicated that correlations between measures of intelligence and personality are small, and it has thus been argued that g is a purely cognitive variable that is independent of personality traits. In a 2007 meta-analysis the correlations between g and the "Big Five" personality traits were found to be as follows:

• conscientiousness -.04
• agreeableness .00
• extraversion .02
• openness .22
• emotional stability .09

The same meta-analysis found a correlation of .20 between self-efficacy and g.^[97][98][99]

Some researchers have argued that the associations between intelligence and personality, albeit modest, are consistent. They have interpreted correlations between intelligence and personality measures in two main ways. The first perspective is that personality traits influence performance on intelligence tests. For example, a person may fail to perform at a maximal level on an IQ test due to his or her anxiety and stress-proneness. The second perspective considers intelligence and personality to be conceptually related, with personality traits determining how people apply and invest their cognitive abilities, leading to knowledge expansion and greater cognitive differentiation.^[97][100]

Creativity

Some researchers believe that there is a threshold level of g below which socially significant creativity is rare, but that otherwise there is no relationship between the two. It has been suggested that this threshold is at least one standard deviation above the population mean. Above the threshold, personality differences are believed to be important determinants of individual variation in creativity.^[101][102]

Others have challenged the threshold theory. While not disputing that opportunity and personal attributes other than intelligence, such as energy and commitment, are important for creativity, they argue that g is positively associated with creativity even at the high end of the ability distribution. The longitudinal Study of Mathematically Precocious Youth has provided evidence for this contention. It has showed that individuals identified by standardized tests as intellectually gifted in early adolescence accomplish creative achievements (for example, securing patents or publishing literary or scientific works) at several times the rate of the general population, and that even within the top 1 percent of cognitive ability, those with higher ability are more likely to make outstanding achievements. The study has also suggested that the level of g acts as a predictor of the level of achievement, while specific cognitive ability patterns predict the realm of achievement.^[103][104]

Challenges

Gf-Gc theory

Raymond Cattell, a student of Charles Spearman's, rejected the unitary g factor model and divided g into two broad, relatively independent domains: fluid intelligence (Gf) and crystallized intelligence (Gc). Gf is conceptualized as a capacity to figure out novel problems, and it is best assessed with tests with little cultural or scholastic content, such as Raven's matrices. Gc can be thought of as consolidated knowledge, reflecting the skills and information that an individual acquires and retains throughout his or her life. Gc is dependent on education and other forms of acculturation, and it is best assessed with tests that emphasize scholastic and cultural knowledge.^[2][41][105] Gf can be thought to primarily consist of current reasoning and problem solving capabilities, while Gc reflects the outcome of previously executed cognitive processes.^[106]

The rationale for the separation of Gf and Gc was to explain individuals' cognitive development over time. While Gf and Gc have been found to be highly correlated, they differ in the way they change over a lifetime. Gf tends to peak at around age 20, slowly declining thereafter. In contrast, Gc is stable or increases across adulthood. A single general factor has been criticized as obscuring this bifurcated pattern of development. Cattell argued that Gf reflected individual differences in the efficiency of the central nervous system. Gc was, in Cattell's thinking, the result of a person "investing" his or her Gf in learning experiences throughout life.^{[2][28][41][107]}

Cattell, together with John Horn, later expanded the Gf-Gc model to include a number of other broad abilities, such as Gq (quantitative reasoning) and Gv (visual-spatial reasoning). While all the broad ability factors in the extended Gf-Gc model are positively correlated and thus would enable the extraction of a higher order g factor, Cattell and Horn maintained that it would be erroneous to posit that a general factor underlies these broad abilities. They argued that g factors computed from different test batteries are not invariant and would give different values of g, and that the correlations among tests arise because it is difficult to test just one ability at a time.^[2][45][108]

However, several researchers have suggested that the Gf-Gc model is compatible with a g-centered understanding of cognitive abilities. For example, John B. Carroll's three-stratum model of intelligence includes both Gf and Gc together with a higher-order g factor. Based on factor analyses of many data sets, some researchers have also argued that Gf and g are one and the same factor and that g factors from different test batteries are substantially invariant provided that the batteries are large and diverse.^{[41][109][110]}

Theories of uncorrelated abilities

Several theorists have proposed that there are intellectual abilities that are uncorrelated with each other. Among the earliest was L.L. Thurstone who created a model of primary mental abilities representing supposedly independent domains of intelligence. However, Thurstone's tests of these abilities were found to produce a strong general factor. He argued that the lack of independence among his tests reflected the difficulty of constructing "factorially pure" tests that measured just one ability. Similarly, J.P. Guilford proposed a model of intelligence that comprised up to 180 distinct, uncorrelated abilities, and claimed to be able to test all of them. Later analyses have shown that the factorial procedures Guilford presented as evidence for his theory did not provide support for it, and that the test data that he claimed provided evidence against g did in fact exhibit the usual pattern of intercorrelations after correction for statistical artifacts.^[111][112]

More recently, Howard Gardner has developed the theory of multiple intelligences. He posits the existence of nine different and independent domains of intelligence, such as mathematical, linguistic, spatial, musical, bodily-kinesthetic, meta-cognitive, and existential intelligences, and contends that individuals who fail in some of them may excel in others. According to Gardner, tests and schools traditionally emphasize only linguistic and logical abilities while neglecting other forms of intelligence. While popular among educationalists, Gardner's theory has been much criticized by psychologists and psychometricians. One criticism is that the theory does violence to both scientific and everyday usages of the word "intelligence." Several researchers have argued that not all of Gardner's intelligences fall within the cognitive sphere. For example, Gardner contends that a successful career in professional sports or popular music reflects bodily-kinesthetic intelligence and musical intelligence, respectively, even though one might usually talk of athletic and musical skills, talents, or abilities instead. Another criticism of Gardner's theory is that many of his purportedly independent domains of intelligence are in fact correlated with each other. Responding to empirical analyses showing correlations between the domains, Gardner has argued that the correlations exist because of the common format of tests and because all tests require linguistic and logical skills. His critics have in turn pointed out that not all IQ tests are administered in the paper-and-pencil format, that aside from linguistic and logical abilities, IQ test batteries contain also measures of, for example, spatial abilities, and that elementary cognitive tasks (for example, inspection time and reaction time) that do not involve linguistic or logical reasoning correlate with conventional IQ batteries, too.^{[62][113][114][115]}

Robert Sternberg, working with various colleagues, has also suggested that intelligence has dimensions independent of g. He argues that there are three classes of intelligence: analytic, practical, and creative. According to Sternberg, traditional psychometric tests measure only analytic intelligence, and should be augmented to test creative and practical intelligence as well. He has devised several tests to this effect. Sternberg equates analytic intelligence with academic intelligence, and contrasts it with practical intelligence, defined as an ability to deal with ill-defined real-life problems. Tacit intelligence is an important component of practical intelligence, consisting of knowledge that is not explicitly taught but is required in many real-life situations. Assessing creativity independent of intelligence tests has traditionally proved difficult, but Sternberg and colleagues have claimed to have created valid tests of creativity, too. The validation of Sternberg's theory requires that the three abilities tested are substantially uncorrelated and have independent predictive validity. Sternberg has conducted many experiments which he claims confirm the validity of his theory, but several researchers have disputed this conclusion. For example, in his reanalysis of a validation study of Sternberg's STAT test, Nathan Brody showed that the predictive validity of the STAT, a test of three allegedly independent abilities, was almost solely due to a single general factor underlying the tests, which Brody equated with the g factor.^[116][117]

Flynn's model

James Flynn has argued that intelligence should be conceptualized at three different levels: brain physiology, cognitive differences between individuals, and social trends in intelligence over time. According to this model, the g factor is a useful concept with respect to individual differences but its explanatory power is limited when the focus of investigation is either brain physiology, or, especially, the effect of social trends on intelligence. Flynn has criticized the notion that cognitive gains over time, or the Flynn effect, are "hollow" if they cannot be shown to be increases in g. He argues that the Flynn effect reflects shifting social priorities and individuals' adaptation to them. To apply the individual differences concept of g to the Flynn effect is to confuse different levels of analysis. On the other hand, according to Flynn, it is also fallacious to deny, by referring to trends in intelligence over time, that some individuals have "better brains and minds" to cope with the cognitive demands of their particular time. At the level of brain physiology, Flynn has emphasized both that localized neural clusters can be affected differently by cognitive exercise, and that there are important factors that affect all neural clusters.^[118]

Other criticisms

Perhaps the most famous critique of the construct of g is that of the paleontologist and biologist Stephen Jay Gould's, presented in his 1981 book The Mismeasure of Man. He argued that psychometricians have fallaciously reified the g factor as a physical thing in the brain, even though it is simply the product of statistical calculations (i.e., factor analysis). He further noted that it is possible to produce factor solutions of cognitive test data that do not contain a g factor yet explain the same amount of information as solutions that yield a g. According to Gould, there is no rationale for preferring one factor solution to another, and factor analysis therefore does not lend support to the existence of an entity like g. More generally, Gould criticized the g theory for abstracting intelligence as a single entity and for ranking people "in a single series of worthiness", arguing that such rankings are used to justify the oppression of disadvantaged groups.^[34][119]

Many researchers have criticized Gould's arguments. For example, they have rejected the accusation of reification, maintaining that the use of extracted factors such as g as potential causal variables whose reality can be supported or rejected by further investigations constitutes a normal scientific practice that in no way distinguishes psychometrics from other sciences. Critics have also suggested that Gould did not understand the purpose of factor analysis, and that he was ignorant of relevant methodological advances in the field. While different factor solutions may be mathematically equivalent in their ability to account for intercorrelations among tests, solutions that yield a g factor are psychologically preferable for several reasons extrinsic to factor analysis, including the phenomenon of the positive manifold, the fact that the same g can emerge from quite different test batteries, the widespread practical validity of g, and the linkage of g to many biological variables.^{[34][35][120]}

John Horn and John McArdle have argued that the modern g theory, as espoused by, for example, Arthur Jensen, is unfalsifiable, because the existence of a common factor like g follows tautologically from positive correlations among tests. They contrasted the modern hierarchical theory of g with Spearman's original two-factor theory which was readily falsifiable (and indeed was falsified).^[28]

See also

• Charles Spearman
• Factor analysis in psychometrics
• Fluid and crystallized intelligence
• Flynn effect
• Intelligence
• Intelligence quotient
• Malleability of intelligence
• Spearman's hypothesis

References

Bibliography

• Ackerman, P. L., Beier, M. E., & Boyle, M. O. (2005). Working memory and intelligence: The same or different constructs? Psychological Bulletin, 131, 30–60. doi:10.1037/0033-2909.131.1.30
• Bartholomew, D.J., Deary, I.J., & Lawn, M. (2009). A New Lease of Life for Thomson's Bonds Model of Intelligence. Psychological Review, 116, 567–579. doi:10.1037/a0016262
• Brody, N. (2006). Geocentric theory: A valid alternative to Gardner's theory of intelligence. In Schaler J. A. (Ed.), Howard Gardner under fire: The rebel psychologist faces his critics. Chicago: Open Court.
• Carroll, J.B. (1995). Reflections on Stephen Jay Gould's The Mismeasure of Man (1981): A Retrospective Review. Intelligence, 21, 121–134.
• Carroll, J.B. (1997). Psychometrics, Intelligence, and Public Perception. Intelligence, 24, 25–52.
• Chabris, C.F. (2007). Cognitive and Neurobiological Mechanisms of the Law of General Intelligence. In Roberts, M. J. (Ed.) Integrating the mind: Domain general versus domain specific processes in higher cognition. Hove, UK: Psychology Press.
• Chabris, C.F., Hebert, B.M, Benjamin, D.J., Beauchamp, J.P., Cesarini, D., van der Loos, M.J.H.M., Johannesson, M., Magnusson, P.K.E., Lichtenstein, P., Atwood, C.S., Freese, J., Hauser, T.S., Hauser, R.M., Christakis, N.A., and Laibson, D. (2012). "Most Reported Genetic Associations with General Intelligence Are Probably False Positives" (PDF). Psychological Science 23 (11): 1314–1323. doi:10.1177/0956797611435528. PMC 3498585. PMID 23012269. 
• Davidson, J.E. & Kemp, I.A. (2011). Contemporary models of intelligence. In R.J. Sternberg & S.B. Kaufman (Eds.), The Cambridge Handbook of Intelligence. New York, NY: Cambridge University Press.
• Deary, I.J. (2012). Intelligence. Annual Review of Psychology, 63, 453–482.
• Deary, I.J. (2001). Intelligence. A Very Short Introduction. Oxford: Oxford University Press. doi:10.1093/actrade/9780192893215.001.0001
• Deary I.J. (2000). Looking Down on Human Intelligence: From Psychometrics to the Brain. Oxford, England: Oxford University Press. doi:10.1093/acprof:oso/9780198524175.001.0001
• Deary, I.J., & Pagliari, C. (1991). The strength of g at different levels of ability: Have Detterman and Daniel rediscovered Spearman's "law of diminishing returns"? Intelligence, 15, 247–250. doi:10.1016/0160-2896(91)90033-A
• Deary, I.J., Egan, V., Gibson, G.J., Brand, C.R., Austin, E., & Kellaghan, T. (1996). Intelligence and the differentiation hypothesis. Intelligence, 23, 105–132. doi:10.1016/S0160-2896(96)90008-2
• Deary, I.J., Spinath, F.M. & Bates, T.C. (2006). Genetics of intelligence. Eur J Hum Genet, 14, 690–700. doi:10.1038/sj.ejhg.5201588
• Deary, I.J., Penke, L., & Johnson, W. (2010). The neuroscience of human intelligence differences. Nature Reviews Neuroscience, 11, 201–211.
• Detterman, D.K., & Daniel, M.H. (1989). Correlations of mental tests with each other and with cognitive variables are highest for low-IQ groups. Intelligence, 13, 349–359. doi:10.1016/S0160-2896(89)80007-8
• Eysenck, H.J. (1995). Creativity as a product of intelligence and personality. In Saklofske, D.H. & Zeidner, M. (Eds.), International Handbook of Personality and Intelligence (pp. 231–247). New York, NY, US: Plenum Press.
• Floyd, R. G., Shands, E. I., Rafael, F. A., Bergeron, R., & McGrew, K. S. (2009). The dependability of general-factor loadings: The effects of factor-extraction methods, test battery composition, test battery size, and their interactions. Intelligence, 37, 453–465.
• Flynn, J. (2011). Secular changes in intelligence. Pages 647–665 in R.J. Sternberg & S.B. Kaufman (eds.), Cambridge Handbook of Intelligence. New York, NY: Cambridge University Press.
• Frey, M. C.; Detterman, D. K. (2003). "Scholastic Assessment or g? The Relationship Between the Scholastic Assessment Test and General Cognitive Ability" (PDF). Psychological Science 15 (6): 373–378. doi:10.1111/j.0956-7976.2004.00687.x. PMID 15147489. 
• Gottfredson, L. S. (1998, Winter). The general intelligence factor. Scientific American Presents, 9(4), 24–29.
• Gottfredson, L. S. (2002). g: Highly general and highly practical. Pages 331–380 in R. J. Sternberg & E. L. Grigorenko (Eds.), The general factor of intelligence: How general is it? Mahwah, NJ: Erlbaum.
• Gottfredson, L.S. (2007). Innovation, fatal accidents, and the evolution of general intelligence. In M. J. Roberts (Ed.), Integrating the mind: Domain general versus domain specific processes in higher cognition (pp. 387–425). Hove, UK: Psychology Press.
• Gottfredson, L.S. (2011). Intelligence and social inequality: Why the biological link? Pp. 538–575 in T. Chamorro-Premuzic, A. Furhnam, & S. von Stumm (Eds.), Handbook of Individual Differences. Wiley-Blackwell.
• Gould, S.J. (1996, Revised Edition). The Mismeasure of Man. New York: W. W. Norton & Company.
• Haworth, C.M.A. et al. (2010). The heritability of general cognitive ability increases linearly from childhood to young adulthood. Mol Psychiatry, 15, 1112–1120. doi:10.1038/mp.2009.55
• Horn, J. L. & McArdle, J.J. (2007). Understanding human intelligence since Spearman. In R. Cudeck & R. MacCallum, (Eds.). Factor Analysis at 100 years (pp. 205–247). Mahwah, NJ: Lawrence Erlbaum Associates, Inc.
• Humphreys, L.G., Rich, S.A. & Davey, T.C. (1985). A Piagetian Test of General Intelligence. Developmental Psychology, 21, 872–877.
• Hunt, E.B. (2011). Human Intelligence. Cambridge, UK: Cambridge University Press.
• Jensen, A.R. (1980). Bias in Mental Testing. New York: The Free Press.
• Jensen, A.R. (1982). The Debunking of Scientific Fossils and Straw Persons. Contemporary Education Review, 1, 121–135.
• Jensen, A.R. (1992). Understanding g in terms of information processing. Educational Psychology Review, 4, 271–308.
• Jensen, A.R. (1998). The g factor: The science of mental ability. Westport, CT: Praeger. ISBN 0-275-96103-6
• Jensen, A.R. (2000). A Nihilistic Philosophy of Science for a Scientific Psychology? Psycoloquy, 11, Issue 088, Article 49.
• Jensen, A.R. (2002). Psychometric g: Definition and substantiation. In R.J. Sternberg & E.L. Grigorenko (Eds.), General factor of intelligence: How general is it? (pp. 39–54). Mahwah, NJ: Erlbaum.
• Johnson, W., Bouchard, T.J., Krueger, R.F., McGue, M. & Gottesman, I.I. (2004). Just one g: Consistent results from three test batteries. Intelligence, 32, 95–107. doi:10.1016/S0160-2896(03)00062-X
• Johnson, W., te Nijenhuis, J. & Bouchard Jr., T. (2008). Still just 1 g: Consistent results from five test batteries. Intelligence, 36, 81–95.
• Judge, T. A., Jackson, C. L., Shaw, J. C., Scott, B. A., and Rich, B. L. (2007). Self-efficacy and work-related performance: The integral role of individual differences. Journal of Applied Psychology, 92, 107–127.
• Kamphaus, R.W., Winsor, A.P., Rowe, E.W., & Kim, S. (2005). A history of intelligence test interpretation. In D.P. Flanagan and P.L. Harrison (Eds.), Contemporary intellectual assessment: Theories, tests, and issues (2nd Ed.) (pp. 23–38). New York: Guilford.
• Kane, M. J., Hambrick, D. Z., & Conway, A. R. A. (2005). Working memory capacity and fluid intelligence are strongly related constructs: Comment on Ackerman, Beier, and Boyle (2004). Psychological Bulletin, 131, 66–71.
• Keith, T.Z., Kranzler, J.H., and Flanagan, D.P. (2001). What does the Cognitive Assessment System (CAS) measure? Joint confirmatory factor analysis of the CAS and the Woodcock-Johnson Tests of Cognitive Ability (3rd Edition). School Psychology Review, 30, 89–119.
• Korb, K. B. (1994). Stephen Jay Gould on intelligence. Cognition, 52, 111–123. doi:10.1016/0010-0277(94)90064-7
• Kovas, Y. & Plomin, R. (2006). Generalist genes: implications for the cognitive sciences. TRENDS in Cognitive Sciences, 10, 198–203.
• Kvist, A. & Gustafsson, J.-E. (2008). The relation between fluid intelligence and the general factor as a function of cultural background: A test of Cattell's Investment theory. Intelligence 36, 422–436.
• Lautrey, J. (2002). Is there a general factor of cognitive development? In Sternberg, R.J. & Grigorenko, E.L. (Eds.), The general factor of intelligence: How general is it? Mahwah, NJ: Erlbaum.
• Lubinski, D. (2009). Exceptional Cognitive Ability: The Phenotype. Behavior Genetics, 39, 350–358, doi:10.1007/s10519-009-9273-0
• Lynn, R. (2003). The Geography of Intelligence. In Nyborg, H. (ed.), The Scientific Study of General Intelligence: Tribute to Arthur R. Jensen (pp. 126–146). Oxford: Pergamon.
• Mackintosh, N.J. (2011). IQ and Human Intelligence. Oxford, UK: Oxford University Press.
• McGrew, K.S. (2005). The Cattell-Horn-Carroll Theory of Cognitive Abilities: Past, Present, and Future. Contemporary Intellectual Assessment: Theories, Tests, and Issues. (pp. 136–181) New York, NY, US: Guilford Press Flanagan, Dawn P. (Ed); Harrison, Patti L. (Ed), (2005). xvii, 667 pp.
• Neisser, U., Boodoo, G., Bouchard Jr., T.J., Boykin, A.W., Brody, N., Ceci, S.J., Halpern, D.F., Loehlin, J.C. & Perloff, R. (1996). "Intelligence: Knowns and Unknowns". American Psychologist, 51, 77–101
• Oberauer, K., Schulze, R., Wilhelm, O., & Süß, H.-M. (2005). Working memory and intelligence – their correlation and their relation: A comment on Ackerman, Beier, and Boyle (2005). Psychological Bulletin, 131, 61–65.
• Penke, L., Denissen, J.J.A., and Miller, G.F. (2007). The Evolutionary Genetics of Personality. European Journal of Personality, 21, 549–587.
• Plomin, R. (2003). Genetics, genes, genomics and g. Molecular Psychiatry, 8, 1–5.
• Plomin, R. & Spinath, F.M. (2004). Intelligence: genetics, genes, and genomics. J Pers Soc Psychol, 86, 112–129.
• Robertson, K.F., Smeets, S., Lubinski, D., & Benbow, C.P. (2010). Beyond the Threshold Hypothesis: Even Among the Gifted and Top Math/Science Graduate Students, Cognitive Abilities, Vocational Interests, and Lifestyle Preferences Matter for Career Choice, Performance, and Persistence. Current Directions in Psychological Science, 19, 346–351.
• Roth, P.L., Bevier, C.A., Bobko, P., Switzer, F.S., III, & Tyler, P. (2001). Ethnic group differences in cognitive ability in employment and educational settings: A meta-analysis. Personnel Psychology, 54, 297–330.
• Rushton, J.P. & Jensen, A.R. (2010). The rise and fall of the Flynn Effect as a reason to expect a narrowing of the Black–White IQ gap. Intelligence, 38, 213–219. doi:10.1016/j.intell.2009.12.002
• Sackett, P.R., Borneman, M.J., and Connelly, B.S. (2008). High-Stakes Testing in Higher Education and Employment. Appraising the Evidence for Validity and Fairness. American Psychologist, 63, 215–227.
• Schmidt, F.L. & Hunter, J. (2004). General Mental Ability in the World of Work: Occupational Attainment and Job Performance. Journal of Personality and Social Psychology, 86, 162–173.
• Spearman, C.E. (1904). "'General intelligence', Objectively Determined And Measured". American Journal of Psychology, 15, 201–293.
• Spearman, C.E. (1927). The Abilities of Man. London: Macmillan.
• Stauffer, J., Ree, M.J., & Carretta, T.R. (1996). Cognitive-Components Tests Are Not Much More than g: An Extension of Kyllonen's Analyses. The Journal of General Psychology, 123, 193–205.
• Sternberg, R. J., Conway, B. E., Ketron, J. L. & Bernstein, M. (1981). People's conception of intelligence. Journal of Personality and Social Psychology, 41, 37–55. doi:10.1037/0022-3514.41.1.37
• von Stumm, S., Chamorro-Premuzic, T., Quiroga, M.Á., and Colom, R. (2009). Separating narrow and general variances in intelligence-personality associations. Personality and Individual Differences, 47, 336–341.
• von Stumm, S., Chamorro-Premuzic, T., Ackerman, P. L. (2011). Re-visiting intelligence-personality associations: Vindicating intellectual investment. In T. Chamorro-Premuzic, S. von Stumm, & A. Furnham (eds.), Handbook of Individual Differences. Chichester, UK: Wiley-Blackwell.
• Tucker-Drob, E.M. (2009). Differentiation of cognitive abilities across the life span. Developmental Psychology, 45, 1097–1118. doi:10.1037/a0015864
• van der Maas, H. L. J., Dolan, C. V., Grasman, R. P. P. P., Wicherts, J. M., Huizenga, H. M., & Raaijmakers, M. E. J. (2006). A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychological Review, 13, 842–860.
• Weinberg, R.A. (1989). Intelligence and IQ. Landmark Issues and Great Debates. American Psychologist, 44, 98–104. doi:10.1037/0003-066X.44.2.98

External links

• The General Intelligence Factor by Linda S. Gottfredson