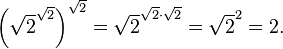Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond[1] and Theodor Schneider. The Gelfond–Schneider theorem answers affirmatively Hilbert's seventh problem.
Statement
- If a and b are algebraic numbers with a ≠ 0,1 and b irrational, then any value of ab is a transcendental number.
Comments
- The values of a and b are not restricted to real numbers; complex numbers are allowed (they are never rational when they have an imaginary part not equal to 0, even if both the real and imaginary parts are rational).
- In general, ab = exp(b log a) is multivalued, where "log" stands for the complex logarithm. This accounts for the phrase "any value of" in the theorem's statement.
- An equivalent formulation of the theorem is the following: if α and γ are nonzero algebraic numbers, and we take any non-zero logarithm of α, then (log γ)/(log α) is either rational or transcendental. This may be expressed as saying that if log α, log γ are linearly independent over the rationals, then they are linearly independent over the algebraic numbers. The generalisation of this statement to more general linear forms in logarithms of several algebraic numbers is in the domain of transcendental number theory.
- If the restriction that a and b be algebraic is removed, the statement does not remain true in general. For example,
- Here, a is √2√2, which (as proven by the theorem itself) is transcendental rather than algebraic. Similarly, if a = 3 and b = (log 2)/(log 3), which is transcendental, then ab = 2 is algebraic. A characterization of the values for a and b, which yield a transcendental ab, is not known.
- Kurt Mahler proved the p-adic analogue of the theorem: if a and b are in Cp, the completion of the algebraic closure of Qp, and they are algebraic over Q, and if |a − 1|p < 1 and |b − 1|p < 1, then (logpα)/(logpb) is either rational or transcendental, where logp is the p-adic logarithm function.
Corollaries
The transcendence of the following numbers follows immediately from the theorem:
- Gelfond–Schneider constant
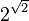 and its square root
and its square root 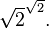
- Gelfond's constant
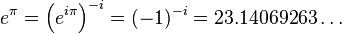 , as well as
, as well as 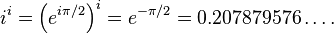
See also
- Lindemann–Weierstrass theorem
- Baker's theorem; an extension of the result
- Schanuel's conjecture; if proven it would imply both the Gelfond–Schneider theorem and the Lindemann–Weierstrass theorem
References
- ↑ Aleksandr Gelfond (1934). "Sur le septième Problème de Hilbert". Bulletin de l'Académie des Sciences de l'URSS. Classe des sciences mathématiques et na VII (4): 623–634.
- Baker, Alan (1975), Transcendental number theory, Cambridge University Press, p. 10, ISBN 978-0-521-20461-3, Zbl 0297.10013
- Feldman, N. I.; Nesterenko, Yu. V. (1998), Transcendental numbers, Encyclopedia of mathematical sciences 44, Springer-Verlag, ISBN 3-540-61467-2, MR 1603604
- Gel'fond, A. O. (1960) [1952], Transcendental and algebraic numbers, Dover Phoenix editions, New York: Dover Publications, ISBN 978-0-486-49526-2, MR 0057921
- LeVeque, William J. (2002) [1956]. Topics in Number Theory, Volumes I and II. New York: Dover Publications. ISBN 978-0-486-42539-9.
- Niven, Ivan (1956). Irrational Numbers. Mathematical Association of America. ISBN 0-88385-011-7.
- Waldschmidt, Michel (2001), "G/g130020", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W., "Gelfond-Schneider Theorem", MathWorld.
External links
This article is issued from Wikipedia - version of the Monday, October 12, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.