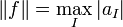Tate algebra

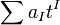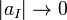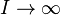In rigid analysis, a branch of mathematics, the Tate algebra over a complete ultrametric field k, named for John Tate, is the subring R of the formal power series ring $k[[t_1, ..., t_n]]$ consisting of $\sum a_I t^I$ such that $|a_I| \to 0$ as $I \to \infty$ . The maximal spectrum of R is then a rigid-analytic space.

Define the Gauss norm of 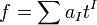$f = \sum a_I t^I$ in R by

\|f\| = \max_I |a_I|

This makes R a Banach k-algebra.

References

http://math.stanford.edu/~conrad/papers/aws.pdf
http://www-math.mit.edu/~kedlaya/18.727/tate-algebras.pdf

This article is issued from Wikipedia - version of the Friday, February 13, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.