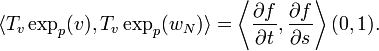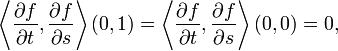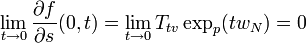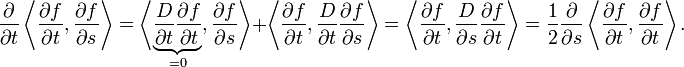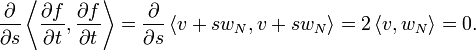Gauss's lemma (Riemannian geometry)
In Riemannian geometry, Gauss's lemma asserts that any sufficiently small sphere centered at a point in a Riemannian manifold is perpendicular to every geodesic through the point. More formally, let M be a Riemannian manifold, equipped with its Levi-Civita connection, and p a point of M. The exponential map is a mapping from the tangent space at p to M:
which is a diffeomorphism in a neighborhood of zero. Gauss' lemma asserts that the image of a sphere of sufficiently small radius in TpM under the exponential map is perpendicular to all geodesics originating at p. The lemma allows the exponential map to be understood as a radial isometry, and is of fundamental importance in the study of geodesic convexity and normal coordinates.
Introduction
We define the exponential map at 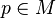 by
by
where 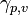 is the unique geodesic with
is the unique geodesic with 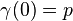 and tangent
and tangent  and
and  is chosen small enough so that for every
is chosen small enough so that for every 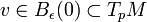 the geodesic
the geodesic 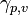 is defined in 1. So, if
is defined in 1. So, if 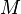 is complete, then, by the Hopf–Rinow theorem,
is complete, then, by the Hopf–Rinow theorem, 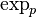 is defined on the whole tangent space.
is defined on the whole tangent space.
Let  be a curve differentiable in
be a curve differentiable in 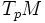 such that
such that  and
and 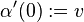 . Since
. Since 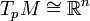 , it is clear that we can choose
, it is clear that we can choose 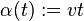 . In this case, by the definition of the differential of the exponential in
. In this case, by the definition of the differential of the exponential in  applied over
applied over  , we obtain:
, we obtain:
So (with the right identification  ) the differential of
) the differential of 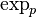 is the identity. By the implicit function theorem,
is the identity. By the implicit function theorem, 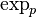 is a diffeomorphism on a neighborhood of
is a diffeomorphism on a neighborhood of 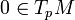 . The Gauss Lemma now tells that
. The Gauss Lemma now tells that 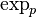 is also a radial isometry.
is also a radial isometry.
The exponential map is a radial isometry
Let 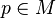 . In what follows, we make the identification
. In what follows, we make the identification 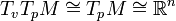 .
.
Gauss's Lemma states:
Let 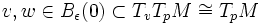 and
and  . Then,
. Then,
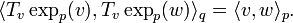
For 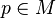 , this lemma means that
, this lemma means that 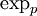 is a radial isometry in the following sense: let
is a radial isometry in the following sense: let 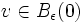 , i.e. such that
, i.e. such that 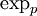 is well defined.
And let
is well defined.
And let 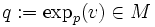 . Then the exponential
. Then the exponential 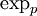 remains an isometry in
remains an isometry in 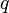 , and, more generally, all along the geodesic
, and, more generally, all along the geodesic 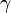 (in so far as
(in so far as  is well defined)! Then, radially, in all the directions permitted by the domain of definition of
is well defined)! Then, radially, in all the directions permitted by the domain of definition of 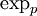 , it remains an isometry.
, it remains an isometry.

Proof
Recall that
We proceed in three steps:
-
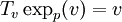 : let us construct a curve
: let us construct a curve
 such that
such that  and
and 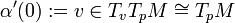 . Since
. Since 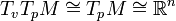 , we can put
, we can put 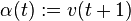 .
We find that, thanks to the identification we have made, and since we are only taking equivalence classes of curves, it is possible to choose
.
We find that, thanks to the identification we have made, and since we are only taking equivalence classes of curves, it is possible to choose  (these are exactly the same curves, but shifted because of the domain of definition
(these are exactly the same curves, but shifted because of the domain of definition  ; however, the identification allows us to gather them around
; however, the identification allows us to gather them around  . Hence,
. Hence,
Now let us calculate the scalar product 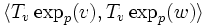 .
.
We separate 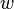 into a component
into a component  parallel to
parallel to  and a component
and a component 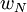 normal to
normal to  . In particular, we put
. In particular, we put 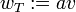 ,
,  .
.
The preceding step implies directly:
We must therefore show that the second term is null, because, according to Gauss's Lemma, we must have:

-
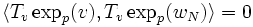 :
:

Let us define the curve
Note that
Let us put:
and we calculate:
and
Hence
We can now verify that this scalar product is actually independent of the variable 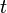 , and therefore that, for example:
, and therefore that, for example:
because, according to what has been given above:
being given that the differential is a linear map. This will therefore prove the lemma.
- We verify that
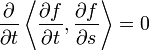 : this is a direct calculation. Since the maps
: this is a direct calculation. Since the maps  are geodesics,
are geodesics,
Since the maps  are geodesics,
the function
are geodesics,
the function 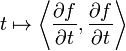 is constant. Thus,
is constant. Thus,
See also
References
- do Carmo, Manfredo (1992), Riemannian geometry, Basel, Boston, Berlin: Birkhäuser, ISBN 978-0-8176-3490-2
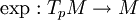


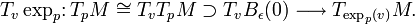
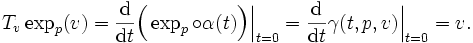
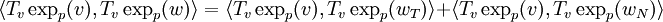
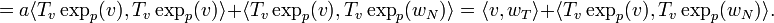
![\alpha \colon [-\epsilon, \epsilon]\times [0,1] \longrightarrow T_pM,\qquad (s,t) \longmapsto tv+tsw_N.](../I/m/b8c0f4c7b12a2e731381f5e5e0e9c84e.png)
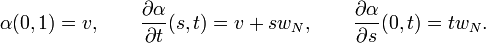
![f \colon [-\epsilon, \epsilon ]\times [0,1] \longrightarrow M,\qquad (s,t)\longmapsto \exp_p(tv+tsw_N),](../I/m/a7a686ba0d78476bcb17b47ce02539fc.png)