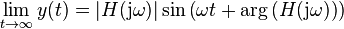Bode plot
In electrical engineering and control theory, a Bode plot /ˈboʊdi/ is a graph of the frequency response of a system. It is usually a combination of a Bode magnitude plot, expressing the magnitude (usually in decibels) of the frequency response, and a Bode phase plot, expressing the phase shift. Both quantities are plotted against a horizontal axis proportional to the logarithm of frequency. Given that the decibel is itself a logarithmic scale, the Bode amplitude plot is log–log plot, whereas the Bode phase plot is a lin-log plot.[1]
As originally conceived by Bode in the 1930s, the plot is only an asymptotic approximation of the frequency response, using straight line segments.[2] However, with the advent of low cost computing, it is often taken nowadays to mean the precise plot of the actual frequency response.
Overview
Among his several important contributions to circuit theory and control theory, engineer Hendrik Wade Bode, while working at Bell Labs in the United States in the 1930s, devised a simple but accurate method for graphing gain and phase-shift plots. These bear his name, Bode gain plot and Bode phase plot. "Bode" is pronounced /ˈboʊdi/ BOH-dee (Dutch: [ˈboːdə]).[3][4]
Bode was faced with the problem of designing stable amplifiers with feedback for use in telephone networks. He developed the graphical design technique of the Bode plots to show the gain margin and phase margin required to maintain stability under variations in circuit characteristics caused during manufacture or during operation.[5] The principles developed were applied to design problems of servomechanisms and other feedback control systems. The Bode plot is an example of analysis in the frequency domain.
Definition
The Bode plot for a linear, time-invariant system with transfer function  (
( being the complex frequency in the Laplace domain) consists of a magnitude plot and a phase plot.
being the complex frequency in the Laplace domain) consists of a magnitude plot and a phase plot.
The Bode magnitude plot is the graph of the function 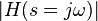 of frequency
of frequency 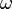 (with
(with 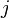 being the imaginary unit). The
being the imaginary unit). The 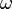 -axis of the magnitude plot is logarithmic and the magnitude is given in decibels, i.e., a value for the magnitude
-axis of the magnitude plot is logarithmic and the magnitude is given in decibels, i.e., a value for the magnitude 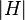 is plotted on the axis at
is plotted on the axis at 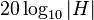 .
.
The Bode phase plot is the graph of the phase of the transfer function 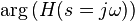 in degrees plotted logarithmically as a function of
in degrees plotted logarithmically as a function of 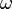 .
.
Examples
Highpass Filter
The one-pole highpass RC-filter has the transfer function
where 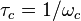 is the inverse of the cut-off frequency
is the inverse of the cut-off frequency 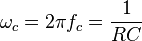 .
.
Magnitude Plot
To obtain the Bode magnitude plot one calculates the magnitude of the transfer function along the imaginary axis
The last equality is obtained using the rules for complex numbers. On the Bode magnitude plot, decibels are used, and the plotted magnitude is:
Phase Plot
To obtain the Bode phase plot one calculates:
Care must be taken that the inverse tangent is set up to return degrees, not radians. The resulting Bode plot is shown in Figure 1(a) for 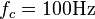 .
.
Lowpass Filter
A passive (unity pass band gain) lowpass RC filter has the following transfer function:
where, again, 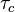 is the inverse of the cut-off frequency. The corresponding Bode Plot is shown in Figure 1(b).
is the inverse of the cut-off frequency. The corresponding Bode Plot is shown in Figure 1(b).
The magnitude and the phase of the transfer function are related. For minimum-phase systems there is a unique relationship between the magnitude and the phase, the Bode gain-phase relationship.[6]
If the transfer function is a rational function with real poles and zeros, then the Bode plot can be approximated with straight lines. These asymptotic approximations are called straight line Bode plots or uncorrected Bode plots and are useful because they can be drawn by hand following a few simple rules. Simple plots can even be predicted without drawing them.
The approximation can be taken further by correcting the value at each cutoff frequency. The plot is then called a corrected Bode plot.
Frequency Response and Bode Plot
This section illustrates that a Bode Plot is a visualization of the frequency response of a system.
Consider a linear, time-invariant system with transfer function  . Assume that the system is subject to a sinusoidal input with frequency
. Assume that the system is subject to a sinusoidal input with frequency 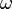 ,
,
that is applied persistently, i.e. from a time 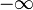 to a time
to a time  . The response will be of the form
. The response will be of the form
i.e., also a sinusoidal signal with amplitude  shifted in phase with respect to the input by a phase
shifted in phase with respect to the input by a phase  .
.
It can be shown[6] that the magnitude of the response is
-
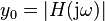
(1)
-
and that the phase shift is
-
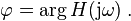
(2)
-
A sketch for the proof of these equations is given in the appendix.
In summary, subjected to an input with frequency 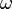 the system responds at the same frequency with an output that is amplified by a factor
the system responds at the same frequency with an output that is amplified by a factor 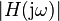 and phase-shifted by
and phase-shifted by 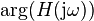 . These quantities, thus, characterize the frequency response and are shown in the Bode plot.
. These quantities, thus, characterize the frequency response and are shown in the Bode plot.
Rules for handmade Bode plot
For many practical problems, the detailed Bode plots can be approximated with straight-line segments that are asymptotes of the precise response. The effect of each of the terms of a multiple element transfer function can be approximated by a set of straight lines on a Bode plot. This allows a graphical solution of the overall frequency response function. Before widespread availability of digital computers, graphical methods were extensively used to reduce the need for tedious calculation; a graphical solution could be used to identify feasible ranges of parameters for a new design.
The premise of a Bode plot is that one can consider the log of a function in the form:
as a sum of the logs of its poles and zeros:
This idea is used explicitly in the method for drawing phase diagrams. The method for drawing amplitude plots implicitly uses this idea, but since the log of the amplitude of each pole or zero always starts at zero and only has one asymptote change (the straight lines), the method can be simplified.
Straight-line amplitude plot
Amplitude decibels is usually done using 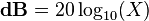 to define decibels. Given a transfer function in the form
to define decibels. Given a transfer function in the form
where 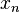 and
and  are constants,
are constants, 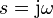 ,
, 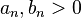 , and
, and  is the transfer function:
is the transfer function:
- at every value of s where
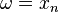 (a zero), increase the slope of the line by
(a zero), increase the slope of the line by 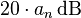 per decade.
per decade. - at every value of s where
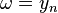 (a pole), decrease the slope of the line by
(a pole), decrease the slope of the line by 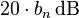 per decade.
per decade. - The initial value of the graph depends on the boundaries. The initial point is found by putting the initial angular frequency
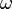 into the function and finding
into the function and finding 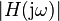 .
. - The initial slope of the function at the initial value depends on the number and order of zeros and poles that are at values below the initial value, and are found using the first two rules.
To handle irreducible 2nd order polynomials, 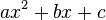 can, in many cases, be approximated as
can, in many cases, be approximated as 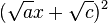 .
.
Note that zeros and poles happen when 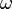 is equal to a certain
is equal to a certain 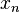 or
or  . This is because the function in question is the magnitude of
. This is because the function in question is the magnitude of 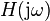 , and since it is a complex function,
, and since it is a complex function, 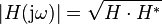 . Thus at any place where there is a zero or pole involving the term
. Thus at any place where there is a zero or pole involving the term 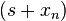 , the magnitude of that term is
, the magnitude of that term is 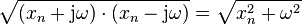 .
.
Corrected amplitude plot
To correct a straight-line amplitude plot:
- at every zero, put a point
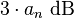 above the line,
above the line, - at every pole, put a point
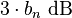 below the line,
below the line, - draw a smooth curve through those points using the straight lines as asymptotes (lines which the curve approaches).
Note that this correction method does not incorporate how to handle complex values of 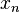 or
or  . In the case of an irreducible polynomial, the best way to correct the plot is to actually calculate the magnitude of the transfer function at the pole or zero corresponding to the irreducible polynomial, and put that dot over or under the line at that pole or zero.
. In the case of an irreducible polynomial, the best way to correct the plot is to actually calculate the magnitude of the transfer function at the pole or zero corresponding to the irreducible polynomial, and put that dot over or under the line at that pole or zero.
Straight-line phase plot
Given a transfer function in the same form as above:
the idea is to draw separate plots for each pole and zero, then add them up. The actual phase curve is given by
![-\arctan \left( \tfrac{\mathrm{Im}[H(s)]}{\mathrm{Re}[H(s)]} \right)](../I/m/a37ac6a433a548636d1748534928038e.png) .
.
To draw the phase plot, for each pole and zero:
- if
 is positive, start line (with zero slope) at
is positive, start line (with zero slope) at 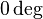
- if
 is negative, start line (with zero slope) at
is negative, start line (with zero slope) at 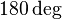
- if the sum of the number of unstable zeros and poles is odd, add 180 degrees to that basis
- at every
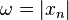 (for stable zeros –
(for stable zeros – 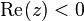 ), increase the slope by
), increase the slope by 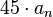 degrees per decade, beginning one decade before
degrees per decade, beginning one decade before 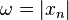 (E.g.:
(E.g.: 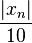 )
) - at every
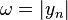 (for stable poles –
(for stable poles – 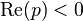 ), decrease the slope by
), decrease the slope by 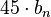 degrees per decade, beginning one decade before
degrees per decade, beginning one decade before 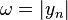 (E.g.:
(E.g.: 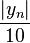 )
) - "unstable" (right half plane) poles and zeros (
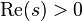 ) have opposite behavior
) have opposite behavior - flatten the slope again when the phase has changed by
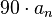 degrees (for a zero) or
degrees (for a zero) or 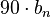 degrees (for a pole),
degrees (for a pole), - After plotting one line for each pole or zero, add the lines together to obtain the final phase plot; that is, the final phase plot is the superposition of each earlier phase plot.
Example
To create a straight-line plot for the lowpass filter, introduced above, one considers the transfer function in terms of the angular frequency:
The above equation is the normalized form of the transfer function. The Bode plot is shown in Figure 1(b) above, and construction of the straight-line approximation is discussed next.
Magnitude plot
The magnitude (in decibels) of the transfer function above, (normalized and converted to angular frequency form), given by the decibel gain expression 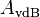 :
:
then plotted versus input frequency 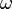 on a logarithmic scale, can be approximated by two lines and it forms the asymptotic (approximate) magnitude Bode plot of the transfer function:
on a logarithmic scale, can be approximated by two lines and it forms the asymptotic (approximate) magnitude Bode plot of the transfer function:
- for angular frequencies below
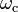 it is a horizontal line at 0 dB since at low frequencies the
it is a horizontal line at 0 dB since at low frequencies the 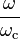 term is small and can be neglected, making the decibel gain equation above equal to zero,
term is small and can be neglected, making the decibel gain equation above equal to zero, - for angular frequencies above
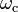 it is a line with a slope of −20 dB per decade since at high frequencies the
it is a line with a slope of −20 dB per decade since at high frequencies the 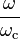 term dominates and the decibel gain expression above simplifies to
term dominates and the decibel gain expression above simplifies to 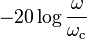 which is a straight line with a slope of
which is a straight line with a slope of 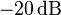 per decade.
per decade.
These two lines meet at the corner frequency. From the plot, it can be seen that for frequencies well below the corner frequency, the circuit has an attenuation of 0 dB, corresponding to a unity pass band gain, i.e. the amplitude of the filter output equals the amplitude of the input. Frequencies above the corner frequency are attenuated – the higher the frequency, the higher the attenuation.
Phase plot
The phase Bode plot is obtained by plotting the phase angle of the transfer function given by
versus 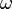 , where
, where 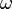 and
and 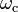 are the input and cutoff angular frequencies respectively. For input frequencies much lower than corner, the ratio
are the input and cutoff angular frequencies respectively. For input frequencies much lower than corner, the ratio 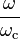 is small and therefore the phase angle is close to zero. As the ratio increases the absolute value of the phase increases and becomes –45 degrees when
is small and therefore the phase angle is close to zero. As the ratio increases the absolute value of the phase increases and becomes –45 degrees when 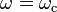 . As the ratio increases for input frequencies much greater than the corner frequency, the phase angle asymptotically approaches −90 degrees. The frequency scale for the phase plot is logarithmic.
. As the ratio increases for input frequencies much greater than the corner frequency, the phase angle asymptotically approaches −90 degrees. The frequency scale for the phase plot is logarithmic.
Normalized plot
The horizontal frequency axis, in both the magnitude and phase plots, can be replaced by the normalized (nondimensional) frequency ratio 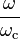 . In such a case the plot is said to be normalized and units of the frequencies are no longer used since all input frequencies are now expressed as multiples of the cutoff frequency
. In such a case the plot is said to be normalized and units of the frequencies are no longer used since all input frequencies are now expressed as multiples of the cutoff frequency 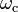 .
.
An example with pole and zero
Figures 2-5 further illustrate construction of Bode plots. This example with both a pole and a zero shows how to use superposition. To begin, the components are presented separately.
Figure 2 shows the Bode magnitude plot for a zero and a low-pass pole, and compares the two with the Bode straight line plots. The straight-line plots are horizontal up to the pole (zero) location and then drop (rise) at 20 dB/decade. The second Figure 3 does the same for the phase. The phase plots are horizontal up to a frequency factor of ten below the pole (zero) location and then drop (rise) at 45°/decade until the frequency is ten times higher than the pole (zero) location. The plots then are again horizontal at higher frequencies at a final, total phase change of 90°.
Figure 4 and Figure 5 show how superposition (simple addition) of a pole and zero plot is done. The Bode straight line plots again are compared with the exact plots. The zero has been moved to higher frequency than the pole to make a more interesting example. Notice in Figure 4 that the 20 dB/decade drop of the pole is arrested by the 20 dB/decade rise of the zero resulting in a horizontal magnitude plot for frequencies above the zero location. Notice in Figure 5 in the phase plot that the straight-line approximation is pretty approximate in the region where both pole and zero affect the phase. Notice also in Figure 5 that the range of frequencies where the phase changes in the straight line plot is limited to frequencies a factor of ten above and below the pole (zero) location. Where the phase of the pole and the zero both are present, the straight-line phase plot is horizontal because the 45°/decade drop of the pole is arrested by the overlapping 45°/decade rise of the zero in the limited range of frequencies where both are active contributors to the phase.
- Example with pole and zero
-
Figure 2: Bode magnitude plot for zero and low-pass pole; curves labeled "Bode" are the straight-line Bode plots
-
Figure 3: Bode phase plot for zero and low-pass pole; curves labeled "Bode" are the straight-line Bode plots
-
Figure 4: Bode magnitude plot for pole-zero combination; the location of the zero is ten times higher than in Figures 2&3; curves labeled "Bode" are the straight-line Bode plots
-
Figure 5: Bode phase plot for pole-zero combination; the location of the zero is ten times higher than in Figures 2&3; curves labeled "Bode" are the straight-line Bode plots
Gain margin and phase margin
Bode plots are used to assess the stability of negative feedback amplifiers by finding the gain and phase margins of an amplifier. The notion of gain and phase margin is based upon the gain expression for a negative feedback amplifier given by
where AFB is the gain of the amplifier with feedback (the closed-loop gain), β is the feedback factor and AOL is the gain without feedback (the open-loop gain). The gain AOL is a complex function of frequency, with both magnitude and phase.[note 1] Examination of this relation shows the possibility of infinite gain (interpreted as instability) if the product βAOL = −1. (That is, the magnitude of βAOL is unity and its phase is −180°, the so-called Barkhausen stability criterion). Bode plots are used to determine just how close an amplifier comes to satisfying this condition.
Key to this determination are two frequencies. The first, labeled here as f180, is the frequency where the open-loop gain flips sign. The second, labeled here f0 dB, is the frequency where the magnitude of the product | β AOL | = 1 (in dB, magnitude 1 is 0 dB). That is, frequency f180 is determined by the condition:
where vertical bars denote the magnitude of a complex number (for example, ![|a + \mathrm{j}b| = \left[ a^2 + b^2 \right]^{\frac12}](../I/m/0e225c67c4b6b2b1e5a8a3bc14a18c7a.png) ), and frequency f0 dB is determined by the condition:
), and frequency f0 dB is determined by the condition:
One measure of proximity to instability is the gain margin. The Bode phase plot locates the frequency where the phase of βAOL reaches −180°, denoted here as frequency f180. Using this frequency, the Bode magnitude plot finds the magnitude of βAOL. If |βAOL|180 = 1, the amplifier is unstable, as mentioned. If AOL|180 < 1, instability does not occur, and the separation in dB of the magnitude of |βAOL|180 from |βAOL| = 1 is called the gain margin. Because a magnitude of one is 0 dB, the gain margin is simply one of the equivalent forms: 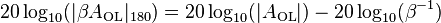 .
.
Another equivalent measure of proximity to instability is the phase margin. The Bode magnitude plot locates the frequency where the magnitude of |βAOL| reaches unity, denoted here as frequency f0 dB. Using this frequency, the Bode phase plot finds the phase of βAOL. If the phase of βAOL( f0 dB) > −180°, the instability condition cannot be met at any frequency (because its magnitude is going to be < 1 when f = f180), and the distance of the phase at f0 dB in degrees above −180° is called the phase margin.
If a simple yes or no on the stability issue is all that is needed, the amplifier is stable if f0 dB < f180. This criterion is sufficient to predict stability only for amplifiers satisfying some restrictions on their pole and zero positions (minimum phase systems). Although these restrictions usually are met, if they are not another method must be used, such as the Nyquist plot.[7][8] Optimal gain and phase margins may be computed using Nevanlinna–Pick interpolation theory.[9]
Examples using Bode plots
Figures 6 and 7 illustrate the gain behavior and terminology. For a three-pole amplifier, Figure 6 compares the Bode plot for the gain without feedback (the open-loop gain) AOL with the gain with feedback AFB (the closed-loop gain). See negative feedback amplifier for more detail.
In this example, AOL = 100 dB at low frequencies, and 1 / β = 58 dB. At low frequencies, AFB ≈ 58 dB as well.
Because the open-loop gain AOL is plotted and not the product β AOL, the condition AOL = 1 / β decides f0 dB. The feedback gain at low frequencies and for large AOL is AFB ≈ 1 / β (look at the formula for the feedback gain at the beginning of this section for the case of large gain AOL), so an equivalent way to find f0 dB is to look where the feedback gain intersects the open-loop gain. (Frequency f0 dB is needed later to find the phase margin.)
Near this crossover of the two gains at f0 dB, the Barkhausen criteria are almost satisfied in this example, and the feedback amplifier exhibits a massive peak in gain (it would be infinity if β AOL = −1). Beyond the unity gain frequency f0 dB, the open-loop gain is sufficiently small that AFB ≈ AOL (examine the formula at the beginning of this section for the case of small AOL).
Figure 7 shows the corresponding phase comparison: the phase of the feedback amplifier is nearly zero out to the frequency f180 where the open-loop gain has a phase of −180°. In this vicinity, the phase of the feedback amplifier plunges abruptly downward to become almost the same as the phase of the open-loop amplifier. (Recall, AFB ≈ AOL for small AOL.)
Comparing the labeled points in Figure 6 and Figure 7, it is seen that the unity gain frequency f0 dB and the phase-flip frequency f180 are very nearly equal in this amplifier, f180 ≈ f0 dB ≈ 3.332 kHz, which means the gain margin and phase margin are nearly zero. The amplifier is borderline stable.
Figures 8 and 9 illustrate the gain margin and phase margin for a different amount of feedback β. The feedback factor is chosen smaller than in Figure 6 or 7, moving the condition | β AOL | = 1 to lower frequency. In this example, 1 / β = 77 dB, and at low frequencies AFB ≈ 77 dB as well.
Figure 8 shows the gain plot. From Figure 8, the intersection of 1 / β and AOL occurs at f0 dB = 1 kHz. Notice that the peak in the gain AFB near f0 dB is almost gone.[note 2][10]
Figure 9 is the phase plot. Using the value of f0 dB = 1 kHz found above from the magnitude plot of Figure 8, the open-loop phase at f0 dB is −135°, which is a phase margin of 45° above −180°.
Using Figure 9, for a phase of −180° the value of f180 = 3.332 kHz (the same result as found earlier, of course[note 3]). The open-loop gain from Figure 8 at f180 is 58 dB, and 1 / β = 77 dB, so the gain margin is 19 dB.
Stability is not the sole criterion for amplifier response, and in many applications a more stringent demand than stability is good step response. As a rule of thumb, good step response requires a phase margin of at least 45°, and often a margin of over 70° is advocated, particularly where component variation due to manufacturing tolerances is an issue.[10] See also the discussion of phase margin in the step response article.
- Examples
-
Figure 6: Gain of feedback amplifier AFB in dB and corresponding open-loop amplifier AOL. Parameter 1/β = 58 dB, and at low frequencies AFB ≈ 58 dB as well. The gain margin in this amplifier is nearly zero because | βAOL| = 1 occurs at almost f = f180°.
-
Figure 7: Phase of feedback amplifier °AFB in degrees and corresponding open-loop amplifier °AOL. The phase margin in this amplifier is nearly zero because the phase-flip occurs at almost the unity gain frequency f = f0 dB where | βAOL| = 1.
-
Figure 8: Gain of feedback amplifier AFB in dB and corresponding open-loop amplifier AOL. In this example, 1 / β = 77 dB. The gain margin in this amplifier is 19 dB.
-
Figure 9: Phase of feedback amplifier AFB in degrees and corresponding open-loop amplifier AOL. The phase margin in this amplifier is 45°.
Bode plotter

The Bode plotter is an electronic instrument resembling an oscilloscope, which produces a Bode diagram, or a graph, of a circuit's voltage gain or phase shift plotted against frequency in a feedback control system or a filter. An example of this is shown in Figure 10. It is extremely useful for analyzing and testing filters and the stability of feedback control systems, through the measurement of corner (cutoff) frequencies and gain and phase margins.
This is identical to the function performed by a vector network analyzer, but the network analyzer is typically used at much higher frequencies.
For education/research purposes, plotting Bode diagrams for given transfer functions facilitates better understanding and getting faster results (see external links).
Related plots
Two related plots that display the same data in different coordinate systems are the Nyquist plot and the Nichols plot. These are parametric plots, with frequency as the input and magnitude and phase of the frequency response as the output. The Nyquist plot displays these in polar coordinates, with magnitude mapping to radius and phase to argument (angle). The Nichols plot displays these in rectangular coordinates, on the log scale.
- Related Plots
-

A Nyquist plot.
-
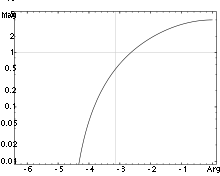
A Nichols plot of the same response.
Appendix
Proof Sketch for the Relation to Frequency Response
This section sketches a proof for the relation between frequency response and the magnitude and phase of the transfer function in Eqs.(1)-(2).
Slightly changing the requirements for Eqs.(1)-(2) one assumes that the input has been applied starting at time 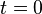 and one calculates the output in the limit
and one calculates the output in the limit  . In this case, the output is given by the convolution
. In this case, the output is given by the convolution
of the input signal with the inverse Laplace transform of the transfer function  . The integral can be split in the following way
. The integral can be split in the following way
where the second term vanishes in the limit  if
if  has certain properties. Thus, inserting the sinusodial input signal one obtains
has certain properties. Thus, inserting the sinusodial input signal one obtains
Since  is a real function this can be written as
is a real function this can be written as
The term in brackets is the definition of the Laplace transform of  at
at 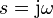 . Inserting the definition in the form
. Inserting the definition in the form 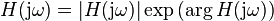 one obtains the output signal
one obtains the output signal
See also
- Analog signal processing
- Phase margin
- Bode's sensitivity integral
- Electrochemical impedance spectroscopy
Notes
- ↑ Ordinarily, as frequency increases the magnitude of the gain drops and the phase becomes more negative, although these are only trends and may be reversed in particular frequency ranges. Unusual gain behavior can render the concepts of gain and phase margin inapplicable. Then other methods such as the Nyquist plot have to be used to assess stability.
- ↑ The critical amount of feedback where the peak in the gain just disappears altogether is the maximally flat or Butterworth design.
- ↑ The frequency where the open-loop gain flips sign f180 does not change with a change in feedback factor; it is a property of the open-loop gain. The value of the gain at f180 also does not change with a change in β. Therefore, we could use the previous values from Figures 6 and 7. However, for clarity the procedure is described using only Figures 8 and 9.
References
- ↑ Dennis L. Feucht (1990). Handbook of Analog Circuit Design. Elsevier Science. p. 194. ISBN 978-1-4832-5938-3.
- ↑ R. K. Rao Yarlagadda (2010). Analog and Digital Signals and Systems. Springer Science & Business Media. p. 243. ISBN 978-1-4419-0034-0.
- ↑ Van Valkenburg, M. E. University of Illinois at Urbana-Champaign, "In memoriam: Hendrik W. Bode (1905-1982)", IEEE Transactions on Automatic Control, Vol. AC-29, No 3., March 1984, pp. 193-194. Quote: "Something should be said about his name. To his colleagues at Bell Laboratories and the generations of engineers that have followed, the pronunciation is boh-dee. The Bode family preferred that the original Dutch be used as boh-dah."
- ↑ "Vertaling van postbode, NL>EN". mijnwoordenboek.nl. Retrieved 2013-10-07.
- ↑ David A. Mindell Between Human and Machine: Feedback, Control, and Computing Before Cybernetics JHU Press, 2004 ISBN 0801880572, pp. 127-131
- 1 2 Skogestad, Sigurd; Postlewaite, Ian (2005). Multivariable Feedback Control. Chichester, West Sussex, England: John Wiley & Sons, Ltd. ISBN 0-470-01167-X.
- ↑ Thomas H. Lee (2004). The design of CMOS radio-frequency integrated circuits (Second ed.). Cambridge UK: Cambridge University Press. p. §14.6 pp. 451–453. ISBN 0-521-83539-9.
- ↑ William S Levine (1996). The control handbook: the electrical engineering handbook series (Second ed.). Boca Raton FL: CRC Press/IEEE Press. p. §10.1 p. 163. ISBN 0-8493-8570-9.
- ↑ Allen Tannenbaum. Invariance and Systems Theory: Algebraic and Geometric Aspects. New York, NY: Springer-Verlag. ISBN 9783540105657.
- 1 2 Willy M C Sansen (2006). Analog design essentials. Dordrecht, The Netherlands: Springer. pp. 157–163. ISBN 0-387-25746-2.
External links
| Wikimedia Commons has media related to Bode plots. |
- Explanation of Bode plots with movies and examples
- How to draw piecewise asymptotic Bode plots
- Summarized drawing rules (PDF)
- Bode plot applet - Accepts transfer function coefficients as input, and calculates magnitude and phase response
- Circuit analysis in electrochemistry
- Tim Green: Operational amplifier stability Includes some Bode plot introduction
- Gnuplot code for generating Bode plot: DIN-A4 printing template (pdf)
- MATLAB function for creating a Bode plot of a system
- MATLAB Tech Talk videos explaining Bode plots and showing how to use them for control design
- Insert the poles and zeros and this website will draw the asymptotic and accurate Bode plots
- Mathematica function for creating the Bode plot
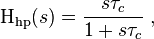
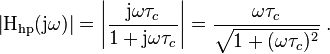
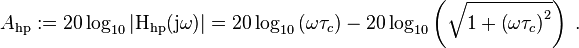
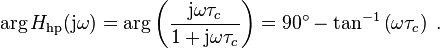
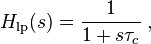
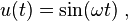
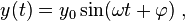
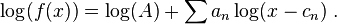
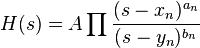
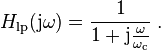
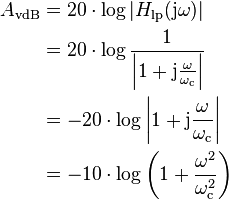
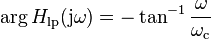
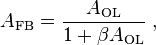
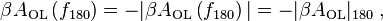
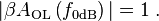
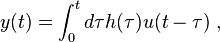
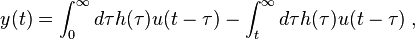
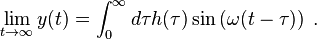
![\lim_{t \to \infty }y(t) = \mathrm{Im} \left\{ \left[ \int_0^\infty d\tau h(\tau) e^{-\mathrm{j} \omega \tau} \right] e^{\mathrm{j} \omega t} \right\} \;.](../I/m/4b050a8f1e18c0b18039dffd75e8f470.png)