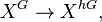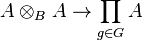G-spectrum

In algebraic topology, a G-spectrum is a spectrum with an action of a (finite) group.

Let X be a spectrum with an action of a finite group G. The important notion is that of the homotopy fixed point set 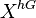$X^{hG}$ . There is always

X^G \to X^{hG},

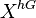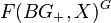a map from the fixed point spectrum to a homotopy fixed point spectrum (because, by definition, $X^{hG}$ is the mapping spectrum $F(BG_+, X)^G$ .)

Example: 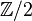$\mathbb{Z}/2$ acts on the complex K-theory KU by taking the conjugate bundle of a complex vector bundle. Then 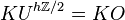$KU^{h\mathbb{Z}/2} = KO$ , the real K-theory.

The cofiber of $X_{hG} \to X^{hG}$ is called the Tate spectrum of X.

G-Galois extension in the sense of Rognes

This notion is due to J. Rognes (Rognes 2008). Let A be an E_∞-ring with an action of a finite group G and B = A^hG its invariant subring. Then B → A (the map of B-algebras in E_∞-sense) is said to be a G-Galois extension if the natural map

A \otimes_B A \to \prod_{g \in G} A

(which generalizes 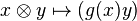$x \otimes y \mapsto (g(x) y)$ in the classical setup) is an equivalence. The extension is faithful if the Bousfield classes of A, B over B are equivalent.

Example: KO → KU is a ℤ./2-Galois extension.

References

Mathew, Akhil; Meier, Lennart (2015). "Affineness and chromatic homotopy theory". arXiv:1311.0514.
Rognes, John (2008), "Galois extensions of structured ring spectra. Stably dualizable groups", Memoirs of the American Mathematical Society 192 (898), doi:10.1090/memo/0898, MR 2387923

External links

http://mathoverflow.net/questions/101011/homology-of-homotopy-fixed-point-spectra

This article is issued from Wikipedia - version of the Monday, September 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

G-spectrum

G-Galois extension in the sense of Rognes

See also

References

External links