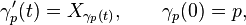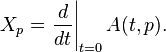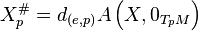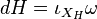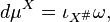Fundamental vector field
In the study of mathematics and especially differential geometry, fundamental vector fields are an instrument that describes the infinitesimal behaviour of a smooth Lie group action on a smooth manifold. Such vector fields find important applications in the study of Lie theory, symplectic geometry, and the study of Hamiltonian group actions.
Motivation
Important to applications in mathematics and physics[1] is the notion of a flow on a manifold. In particular, if  is a smooth manifold and
is a smooth manifold and  is a smooth vector field, one is interested in finding integral curves to
is a smooth vector field, one is interested in finding integral curves to  . More precisely, given
. More precisely, given 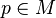 one is interested in curves
one is interested in curves  such that
such that
for which local solutions are guaranteed by the Existence and Uniqueness Theorem of Ordinary Differential Equations. If  is furthermore a complete vector field, then the flow of
is furthermore a complete vector field, then the flow of  , defined as the collection of all integral curves for
, defined as the collection of all integral curves for  , is a diffeomorphism of
, is a diffeomorphism of  . The flow
. The flow 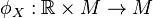 given by
given by 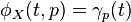 is in fact an action of the additive Lie group
is in fact an action of the additive Lie group 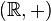 on
on  .
.
Conversely, every smooth action 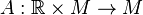 defines a complete vector field
defines a complete vector field  via the equation
via the equation
It is then a simple result[2] that there is a bijective correspondence between  actions on
actions on  and complete vector fields on
and complete vector fields on  .
.
In the language of flow theory, the vector field  is called the infinitesimal generator.[3] Intuitively, the behaviour of the flow at each point corresponds to the "direction" indicated by the vector field. It is a natural question to ask whether one may establish a similar correspondence between vector fields and more arbitrary Lie group actions on
is called the infinitesimal generator.[3] Intuitively, the behaviour of the flow at each point corresponds to the "direction" indicated by the vector field. It is a natural question to ask whether one may establish a similar correspondence between vector fields and more arbitrary Lie group actions on  .
.
Definition
Let  be a Lie group with corresponding Lie algebra
be a Lie group with corresponding Lie algebra 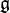 . Furthermore, let
. Furthermore, let  be a smooth manifold endowed with a smooth action
be a smooth manifold endowed with a smooth action 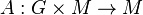 . Denote the map
. Denote the map 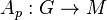 such that
such that 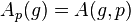 , called the orbit map of
, called the orbit map of  corresponding to
corresponding to  .[4] For
.[4] For 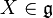 , the fundamental vector field
, the fundamental vector field 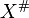 corresponding to
corresponding to  is any of the following equivalent definitions:[2][4][5]
is any of the following equivalent definitions:[2][4][5]
where 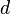 is the differential of a smooth map and
is the differential of a smooth map and 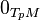 is the zero vector in the vector space
is the zero vector in the vector space  .
.
The map 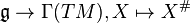 can then be shown to be a Lie algebra homomorphism.[5]
can then be shown to be a Lie algebra homomorphism.[5]
Applications
Lie groups
The Lie algebra of a Lie group  may be identified with either the left- or right-invariant vector fields on
may be identified with either the left- or right-invariant vector fields on  . It is a well known result[3] that such vector fields are isomorphic to
. It is a well known result[3] that such vector fields are isomorphic to 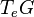 , the tangent space at identity. In fact, if we let
, the tangent space at identity. In fact, if we let  act on itself via right-multiplication, the corresponding fundamental vector fields are precisely the left-invariant vector fields.
act on itself via right-multiplication, the corresponding fundamental vector fields are precisely the left-invariant vector fields.
Hamiltonian group actions
In the motivation, it was shown that there is a bijective correspondence between smooth 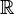 actions and complete vector fields. Similarly, there is a bijective correspondence between symplectic actions (the induced diffeomorphisms are all symplectomorphisms) and complete symplectic vector fields.
actions and complete vector fields. Similarly, there is a bijective correspondence between symplectic actions (the induced diffeomorphisms are all symplectomorphisms) and complete symplectic vector fields.
A closely related idea is that of Hamiltonian vector fields. Given a symplectic manifold 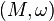 , we say that
, we say that  is a Hamiltonian vector field if there exists a smooth function
is a Hamiltonian vector field if there exists a smooth function 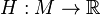 satisfying
satisfying
where the map  is the interior product. This motivatives the definition of a Hamiltonian group action as follows: If
is the interior product. This motivatives the definition of a Hamiltonian group action as follows: If  is a Lie group with Lie algebra
is a Lie group with Lie algebra 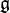 and
and 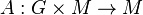 is a group action of
is a group action of  on a smooth manifold
on a smooth manifold  , then we say that
, then we say that  is a Hamiltonian group action if there exists a moment map
is a Hamiltonian group action if there exists a moment map 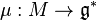 such that for each
such that for each 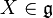 ,
,
where 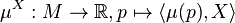 and
and 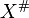 is the fundamental vector field of
is the fundamental vector field of 
References
- ↑ Hou, Bo-Yu (1997), Differential Geometry for Physicists, World Scientific Publishing Company, ISBN 978-9810231057
- ↑ 2.0 2.1 Canas da Silva, Ana (2008). Lectures on Symplectic Geometry. Springer. ISBN 978-3540421955.
- ↑ 3.0 3.1 Lee, John (2003). Introduction to Smooth Manifolds. Springer. ISBN 0-387-95448-1.
- ↑ 4.0 4.1 Audin, Michèle (2004). Torus Actions on Symplectic manifolds. Birkhäuser. ISBN 3-7643-2176-8.
- ↑ 5.0 5.1 Libermann, Paulette; Marle, Charles-Michel (1987). Symplectic Geometry and Analytical Mechanics. Springer. ISBN 978-9027724380.