Fundamental group scheme

In mathematics, the fundamental group scheme is a group scheme canonically associated to a scheme over a Dedekind scheme (e.g. the spectrum of a field or the spectrum of a discrete valuation ring). It is a generalisation of the étale fundamental group. Although its existence was conjectured by Alexander Grothendieck, the first construction is due to Madhav Nori,[1][2] who only worked on schemes over fields. A generalisation to schemes over Dedekind schemes is due to Carlo Gasbarri.[3]

First definition

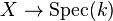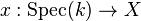Let k be a perfect field and X\to \text{Spec}(k) a faithfully flat and proper morphism of schemes with X a reduced and connected scheme. Assume the existence of a section x:\text{Spec}(k)\to X, then the fundamental group scheme 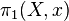\pi_1(X,x) of X in x is defined as the affine group scheme naturally associated to the neutral tannakian category (over k) of essentially finite vector bundles over X.

Second definition

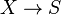Let S be a Dedekind scheme, X any connected scheme (not necessarily reduced)[4] and X\to S a faithfully flat morphism of finite type (not necessarily proper). Assume the existence of a section 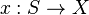x:S\to X. Once we prove that the category of isomorphism classes of torsors over X (pointed over x) under the action of finite and flat S-group schemes is cofiltered then we define the universal torsor (pointed over x) as the projective limit of all the torsors of that category. 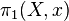The S-group scheme acting on it is called the fundamental group scheme and denoted by \pi_1(X,x) (when S is the spectrum of a perfect field the two definitions coincide so that no confusion can arise).

See also

Notes

  1. ↑ M. V. Nori On the Representations of the Fundamental Group, Compositio Mathematica, Vol. 33, Fasc. 1, (1976), p. 29-42
  2. ↑ T. Szamuely Galois Groups and Fundamental Groups. Cambridge Studies in Advanced Mathematics, Vol. 117 (2009)
  3. ↑ C. Gasbarri, Heights of Vector Bundles and the Fundamental Group Scheme of a Curve, Duke Mathematical Journal, Vol. 117, No. 2, (2003) p. 287-311
  4. ↑ M. Antei, The fundamental group scheme of a non reduced scheme, Bulletin des Sciences Mathématiques, Volume 135, Issue 5, July–August 2011, Pages 531-539.
This article is issued from Wikipedia - version of the Thursday, December 11, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.