Functional renormalization group
In theoretical physics, functional renormalization group (FRG) is an implementation of the renormalization group (RG) concept which is used in quantum and statistical field theory, especially when dealing with strongly interacting systems. The method combines functional methods of quantum field theory with the intuitive renormalization group idea of Kenneth G. Wilson. This technique allows to interpolate smoothly between the known microscopic laws and the complicated macroscopic phenomena in physical systems. In this sense, it bridges the transition from simplicity of microphysics to complexity of macrophysics. Figuratively speaking, FRG acts as a microscope with a variable resolution. One starts with a high-resolution picture of the known microphysical laws and subsequently decreases the resolution to obtain a coarse-grained picture of macroscopic collective phenomena. The method is nonperturbative, meaning that it does not rely on an expansion in a small coupling constant. Mathematically, FRG is based on an exact functional differential equation for a scale-dependent effective action.
The flow equation for the effective action
In quantum field theory, the effective action  is an analogue of the classical action functional
is an analogue of the classical action functional 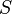 and depends on the fields of a given theory. It includes all quantum and thermal fluctuations. Variation of
and depends on the fields of a given theory. It includes all quantum and thermal fluctuations. Variation of  yields exact quantum field equations, for example for cosmology or the electrodynamics of superconductors. Mathematically,
yields exact quantum field equations, for example for cosmology or the electrodynamics of superconductors. Mathematically,  is the generating functional of the one-particle irreducible Feynman diagrams. Interesting physics, as propagators and effective couplings for interactions, can be straightforwardly extracted from it. In a generic interacting field theory the effective action
is the generating functional of the one-particle irreducible Feynman diagrams. Interesting physics, as propagators and effective couplings for interactions, can be straightforwardly extracted from it. In a generic interacting field theory the effective action  , however, is difficult to obtain. FRG provides a practical tool to calculate
, however, is difficult to obtain. FRG provides a practical tool to calculate  employing the renormalization group concept.
employing the renormalization group concept.
The central object in FRG is a scale-dependent effective action functional 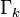 often called average action or flowing action. The dependence on the RG sliding scale
often called average action or flowing action. The dependence on the RG sliding scale  is introduced by adding a regulator (infrared cutoff)
is introduced by adding a regulator (infrared cutoff) 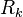 to the full inverse propagator
to the full inverse propagator 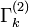 . Roughly speaking, the regulator
. Roughly speaking, the regulator 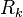 decouples slow modes with momenta
decouples slow modes with momenta 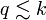 by giving them a large mass, while high momentum modes are not affected. Thus,
by giving them a large mass, while high momentum modes are not affected. Thus, 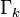 includes all quantum and statistical fluctuations with momenta
includes all quantum and statistical fluctuations with momenta 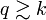 . The flowing action
. The flowing action 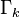 obeys the exact functional flow equation
obeys the exact functional flow equation
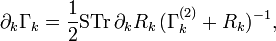
derived by Christof Wetterich in 1993 and Tim R. Morris in 1994. Here 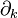 denotes a derivative with respect to the RG scale
denotes a derivative with respect to the RG scale  at fixed values of the fields.
The functional differential equation for
at fixed values of the fields.
The functional differential equation for 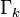 must be supplemented with the initial condition
must be supplemented with the initial condition 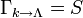 , where the "classical action"
, where the "classical action" 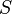 describes the physics at the microscopic ultraviolet scale
describes the physics at the microscopic ultraviolet scale 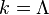 . Importantly, in the infrared limit
. Importantly, in the infrared limit 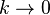 the full effective action
the full effective action 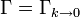 is obtained. In the Wetterich equation
is obtained. In the Wetterich equation 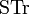 denotes a supertrace which sums over momenta, frequencies, internal indices, and fields (taking bosons with a plus and fermions with a minus sign). The exact flow equation for
denotes a supertrace which sums over momenta, frequencies, internal indices, and fields (taking bosons with a plus and fermions with a minus sign). The exact flow equation for 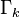 has a one-loop structure. This is an important simplification compared to perturbation theory, where multi-loop diagrams must be included. The second functional derivative
has a one-loop structure. This is an important simplification compared to perturbation theory, where multi-loop diagrams must be included. The second functional derivative 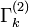 is the full inverse field propagator modified by the presence of the regulator
is the full inverse field propagator modified by the presence of the regulator 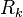 .
.
The renormalization group evolution of 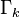 can be illustrated in the theory space, which is a multi-dimensional space of all possible running couplings
can be illustrated in the theory space, which is a multi-dimensional space of all possible running couplings 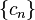 allowed by the symmetries of the problem. As schematically shown in the figure, at the microscopic ultraviolet scale
allowed by the symmetries of the problem. As schematically shown in the figure, at the microscopic ultraviolet scale 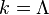 one starts with the initial condition
one starts with the initial condition 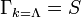 .
.

As the sliding scale  is lowered, the flowing action
is lowered, the flowing action 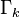 evolves in the theory space according to the functional flow equation. The choice of the regulator
evolves in the theory space according to the functional flow equation. The choice of the regulator 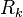 is not unique, which introduces some scheme dependence into the renormalization group flow. For this reason, different choices of the regulator
is not unique, which introduces some scheme dependence into the renormalization group flow. For this reason, different choices of the regulator 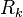 correspond to the different paths in the figure. At the infrared scale
correspond to the different paths in the figure. At the infrared scale 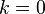 , however, the full effective action
, however, the full effective action 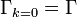 is recovered for every choice of the cut-off
is recovered for every choice of the cut-off 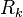 , and all trajectories meet at the same point in the theory space.
, and all trajectories meet at the same point in the theory space.
In most cases of interest the Wetterich equation can only be solved approximately. Usually some type of expansion of 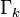 is performed, which is then truncated at finite order leading to a finite system of ordinary differential equations. Different systematic expansion schemes (such as the derivative expansion, vertex expansion, etc.) were developed. The choice of the suitable scheme should be physically motivated and depends on a given problem. The expansions do not necessarily involve a small parameter (like an interaction coupling constant) and thus they are, in general, of nonperturbative nature.
is performed, which is then truncated at finite order leading to a finite system of ordinary differential equations. Different systematic expansion schemes (such as the derivative expansion, vertex expansion, etc.) were developed. The choice of the suitable scheme should be physically motivated and depends on a given problem. The expansions do not necessarily involve a small parameter (like an interaction coupling constant) and thus they are, in general, of nonperturbative nature.
Aspects of functional renormalization
- The Wetterich flow equation is an exact equation. However, in practice, the functional differential equation must be truncated, i.e. it must be projected to functions of a few variables or even onto some finite-dimensional sub-theory space. As in every nonperturbative method, the question of error estimate is nontrivial in functional renormalization. One way to estimate the error in FRG is to improve the truncation in successive steps, i.e. to enlarge the sub-theory space by including more and more running couplings. The difference in the flows for different truncations gives a good estimate of the error. Alternatively, one can use different regulator functions
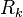 in a given (fixed) truncation and determine the difference of the RG flows in the infrared for the respective regulator choices. If bosonization is used, one can check the insensitivity of final results with respect to different bosonization procedures.
in a given (fixed) truncation and determine the difference of the RG flows in the infrared for the respective regulator choices. If bosonization is used, one can check the insensitivity of final results with respect to different bosonization procedures.
- In FRG, as in all RG methods, a lot of insight about a physical system can be gained from the topology of RG flows. Specifically, identification of fixed points of the renormalization group evolution is of great importance. Near fixed points the flow of running couplings effectively stops and RG
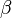 -functions approach zero. The presence of (partially) stable infrared fixed points is closely connected to the concept of universality. Universality manifests itself in the observation that some very distinct physical systems have the same critical behavior. For instance, to good accuracy, critical exponents of the liquid–gas phase transition in water and the ferromagnetic phase transition in magnets are the same. In the renormalization group language, different systems from the same universality class flow to the same (partially) stable infrared fixed point. In this way macrophysics becomes independent of the microscopic details of the particular physical model.
-functions approach zero. The presence of (partially) stable infrared fixed points is closely connected to the concept of universality. Universality manifests itself in the observation that some very distinct physical systems have the same critical behavior. For instance, to good accuracy, critical exponents of the liquid–gas phase transition in water and the ferromagnetic phase transition in magnets are the same. In the renormalization group language, different systems from the same universality class flow to the same (partially) stable infrared fixed point. In this way macrophysics becomes independent of the microscopic details of the particular physical model.
- Compared to the perturbation theory, functional renormalization does not make a strict distinction between renormalizable and nonrenormalizable couplings. All running couplings that are allowed by symmetries of the problem are generated during the FRG flow. However, the nonrenormalizable couplings approach partial fixed points very quickly during the evolution towards the infrared, and thus the flow effectively collapses on a hypersurface of the dimension given by the number of renormalizable couplings. Taking the nonrenormalizable couplings into account allows to study nonuniversal features that are sensitive to the concrete choice of the microscopic action
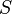 and the finite ultraviolet cutoff
and the finite ultraviolet cutoff 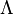 .
.
- The Wetterich equation can be obtained from the Legendre transformation of the Polchinski functional equation, derived by Joseph Polchinski in 1984. The concept of the effective average action, used in FRG, is, however, more intuitive than the flowing bare action in the Polchinski equation. In addition, the FRG method proved to be more suitable for practical calculations.
- Typically, low-energy physics of strongly interacting systems is described by macroscopic degrees of freedom (i.e. particle excitations) which are very different from microscopic high-energy degrees of freedom. For instance, quantum chromodynamics is a field theory of interacting quarks and gluons. At low energies, however, proper degrees of freedom are baryons and mesons. Another example is the BEC/BCS crossover problem in condensed matter physics. While the microscopic theory is defined in terms of two-component nonrelativistic fermions, at low energies a composite (particle-particle) dimer becomes an additional degree of freedom, and it is advisable to include it explicitly in the model. The low-energy composite degrees of freedom can be introduced in the description by the method of partial bosonization (Hubbard-Stratonovich transformation). This transformation, however, is done once and for all at the UV scale
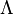 . In FRG a more efficient way to incorporate macroscopic degrees of freedom was introduced, which is known as flowing bosonization or rebosonization. With the help of a scale-dependent field transformation, this allows to perform the Hubbard-Stratonovich transformation continuously at all RG scales
. In FRG a more efficient way to incorporate macroscopic degrees of freedom was introduced, which is known as flowing bosonization or rebosonization. With the help of a scale-dependent field transformation, this allows to perform the Hubbard-Stratonovich transformation continuously at all RG scales  .
.
Functional renormalization-group for Wick-ordered effective interaction
Contrary to the flow equation for the effective action, this scheme is formulated for the effective interaction
![\mathcal{V}[\eta ,\eta ^{+}] =-\ln Z[G_{0}^{-1} \eta , G_{0}^{-1}\eta ^{+}]-\eta G_{0}^{-1}\eta ^{+}](../I/m/17acb3e0229f5f5eb0f78996941c1701.png)
which generates n-particle interaction vertices, amputated by the bare propagators 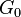 ;
;
![Z[\eta ,\eta ^{+}]](../I/m/0e7d7a557beea917ffad435e348193cc.png) is the "standard" generating functional for the n-particle Green functions.
is the "standard" generating functional for the n-particle Green functions.
The Wick ordering of effective interaction with respect to Green function  can be defined by
can be defined by
![\mathcal{W}[\eta ,\eta ^{+}]=\exp(-\Delta _D)\mathcal{V}[\eta ,\eta ^{+}]](../I/m/f2178fd606ff38ffa071814b52abec13.png) .
.
where 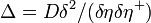 is the Laplacian in the field space. This operation is similar to Normal order and excludes from the interaction all possible terms, formed by a convolution of source fields with respective Green function D. Introducing some cutoff
is the Laplacian in the field space. This operation is similar to Normal order and excludes from the interaction all possible terms, formed by a convolution of source fields with respective Green function D. Introducing some cutoff 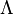 the Polchinskii equation
the Polchinskii equation
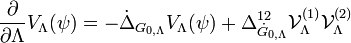
takes the form of the Wick-ordered equation
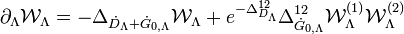
where
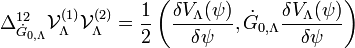
Applications
The method was applied to numerous problems in physics, e.g.:
- In statistical field theory, FRG provided a unified picture of phase transitions in classical linear
 -symmetric scalar theories in different dimensions
-symmetric scalar theories in different dimensions  , including critical exponents for
, including critical exponents for 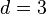 and the Berezinskii-Kosterlitz-Thouless phase transition for
and the Berezinskii-Kosterlitz-Thouless phase transition for 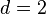 ,
,  .
.
- In gauge quantum field theory, FRG was used, for instance, to investigate the chiral phase transition and infrared properties of QCD and its large-flavor extensions.
- In condensed matter physics, the method proved to be successful to treat lattice models (e.g. the Hubbard model or frustrated magnetic systems), repulsive Bose gas, BEC/BCS crossover for two-component Fermi gas, Kondo effect, disordered systems and nonequlibrium phenomena.
- Application of FRG to gravity provided solid arguments in favor of nonperturbative renormalizability of quantum gravity in four spacetime dimensions, known as the asymptotic safety scenario.
- In mathematical physics FRG was used to prove renormalizability of different field theories.
See also
- Renormalization group
- Renormalization
- Critical phenomena
- Scale invariance
- Asymptotic safety in quantum gravity
References
Papers
- C. Wetterich, C (1993), "Exact evolution equation for the effective potential", Phys. Lett. B 301: 90, Bibcode:1993PhLB..301...90W, doi:10.1016/0370-2693(93)90726-X
- T. Morris, T (1994), "The Exact renormalization group and approximate solutions", Int.J.Mod.Phys. A9 (1994) 2411–2450 A9: 39, Bibcode:1994IJMPA...9.2411M, doi:10.1142/S0217751X94000972
- J. Polchinski, J (1984), "Renormalization and Effective Lagrangians", Nucl. Phys. B 231 (2): 269, Bibcode:1984NuPhB.231..269P, doi:10.1016/0550-3213(84)90287-6
- M. Reuter, M. (1998), "Nonperturbative evolution equation for quantum gravity", Phys. Rev. D 57 (2): 971, arXiv:hep-th/9605030, Bibcode:1998PhRvD..57..971R, doi:10.1103/PhysRevD.57.971
Pedagogic reviews
- J. Berges, N. Tetradis, and C. Wetterich (2002), "Non-perturbative renormalization flow in quantum field theory and statistical mechanics", Phys. Rept. 363 (4–6): 223, arXiv:hep-ph/0005122, Bibcode:2002PhR...363..223B, doi:10.1016/S0370-1573(01)00098-9
- J. Polonyi, Janos (2003), "Lectures on the functional renormalization group method", Central Eur. J. Phys. 1: 1, arXiv:hep-th/0110026, Bibcode:2003CEJPh...1....1P, doi:10.2478/BF02475552
- H.Gies (2006). "Introduction to the functional RG and applications to gauge theories". arXiv:hep-ph/0611146 [hep-ph].
- B. Delamotte (2007). "An introduction to the nonperturbative renormalization group". arXiv:cond-mat/0702365 [cond-mat.stat-mech].
- M. Salmhofer, and C. Honerkamp, Manfred; Honerkamp, Carsten (2001), "Fermionic renormalization group flows: Technique and theory", Prog. Theor. Phys. 105: 1, Bibcode:2001PThPh.105....1S, doi:10.1143/PTP.105.1
- M. Reuter and F. Saueressig; Frank Saueressig (2007). "Functional Renormalization Group Equations, Asymptotic Safety, and Quantum Einstein Gravity". arXiv:0708.1317 [hep-th].