Full and faithful functors

In category theory, a faithful functor (resp. a full functor) is a functor that is injective (resp. surjective) when restricted to each set of morphisms that have a given source and target.

Formal definitions

Explicitly, let C and D be (locally small) categories and let F : C → D be a functor from C to D. The functor F induces a function

F_{X,Y}\colon\mathrm{Hom}_{\mathcal C}(X,Y)\rightarrow\mathrm{Hom}_{\mathcal D}(F(X),F(Y))

for every pair of objects X and Y in C. The functor F is said to be

faithful if F_X,Y is injective^[1]^[2]
full if F_X,Y is surjective^[2]^[3]
fully faithful if F_X,Y is bijective

for each X and Y in C.

Properties

A faithful functor need not be injective on objects or morphisms. That is, two objects X and X′ may map to the same object in D (which is why the range of a full and faithful functor is not necessarily isomorphic to C), and two morphisms f : X → Y and f′ : X′ → Y′ (with different domains/codomains) may map to the same morphism in D. Likewise, a full functor need not be surjective on objects or morphisms. There may be objects in D not of the form FX for some X in C. Morphisms between such objects clearly cannot come from morphisms in C.

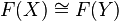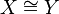A full and faithful functor is necessarily bijective on objects up to isomorphism. That is, if F : C → D is a full and faithful functor and $F(X)\cong F(Y)$ then $X \cong Y$ .

Examples

The forgetful functor U : Grp → Set is faithful as each group maps to a unique set and the group homomorphism are a subset of the functions. This functor is not full as there are functions between groups which are not group homomorphisms. A category with a faithful functor to Set is (by definition) a concrete category; in general, that forgetful functor is not full.

The inclusion functor Ab → Grp is fully faithful, since each abelian group maps to a unique group, and any group homomorphism between abelian groups is preserved in Grp.

Notes

↑ Mac Lane (1971), p. 15
1 2 Jacobson (2009), p. 22
↑ Mac Lane (1971), p. 14

References

Mac Lane, Saunders (September 1998). Categories for the Working Mathematician (second ed.). Springer. ISBN 0-387-98403-8.
Jacobson, Nathan (2009). Basic algebra 2 (2nd ed.). Dover. ISBN 978-0-486-47187-7.

Functor types

Additive Adjoint Derived Diagonal Enriched Essentially surjective Exact Faithful Forgetful Full Logical Monoidal Representable Smooth

This article is issued from Wikipedia - version of the Tuesday, November 03, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.