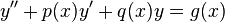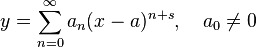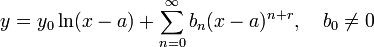Fuchs' theorem

In mathematics, Fuchs' theorem, named after Lazarus Fuchs, states that a second order differential equation of the form

y'' + p(x)y'+q(x)y=g(x)\;

has a solution expressible by a generalised Frobenius series when 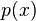$p(x)$ , $q(x)$ and $g(x)$ are analytic at $x=a$ or $a$ is a regular singular point. That is, any solution to this second order differential equation can be written as

y = \sum_{n=0}^\infty a_n (x-a)^{n+s} , \quad a_0 \neq 0

for some real s, or

y = y_0 \ln (x-a) + \sum_{n=0}^\infty b_n(x-a)^{n+r}, \quad b_0 \neq 0

for some real r, where y₀ is a solution of the first kind.

Its radius of convergence is at least as large as the minimum of the radii of convergence of 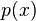$p(x)$ , $q(x)$ and $g(x)$ .

References

Asmar, Nakhlé H. (2005), Partial differential equations with Fourier series and boundary value problems, Upper Saddle River, NJ: Pearson Prentice Hall, ISBN 0-13-148096-0 .
Butkov, Eugene (1995), Mathematical Physics, Reading, MA: Addison-Wesley, ISBN 0-201-00727-4 .

This article is issued from Wikipedia - version of the Saturday, January 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Fuchs' theorem

See also

References