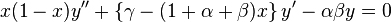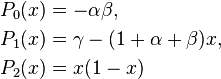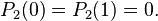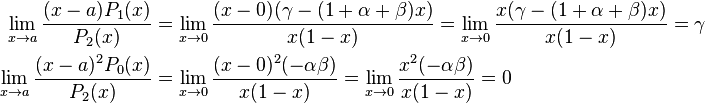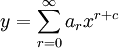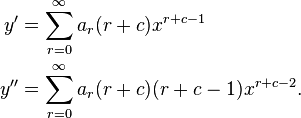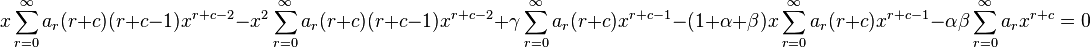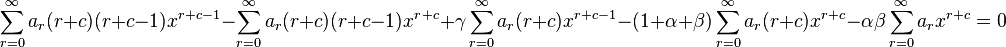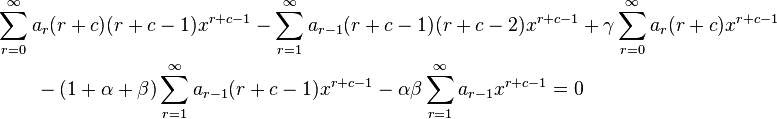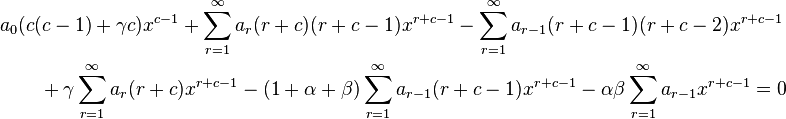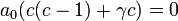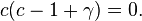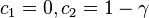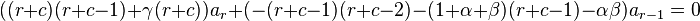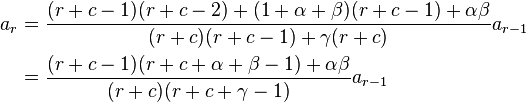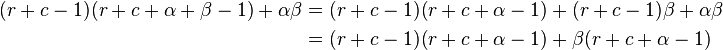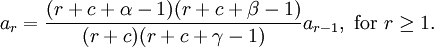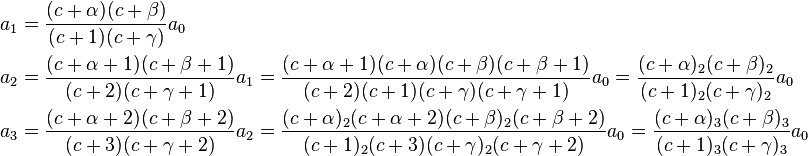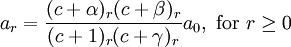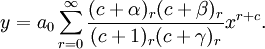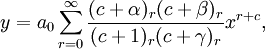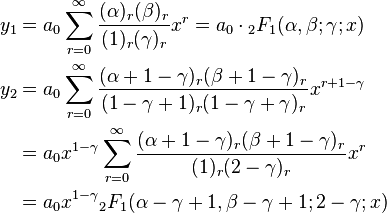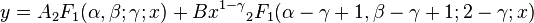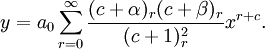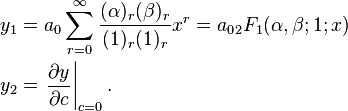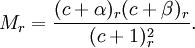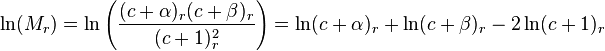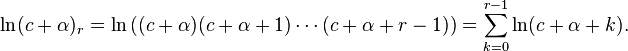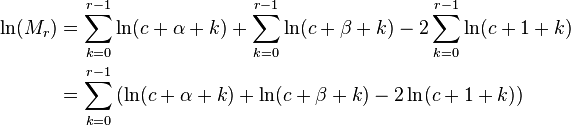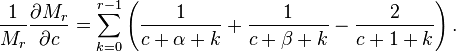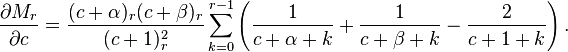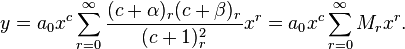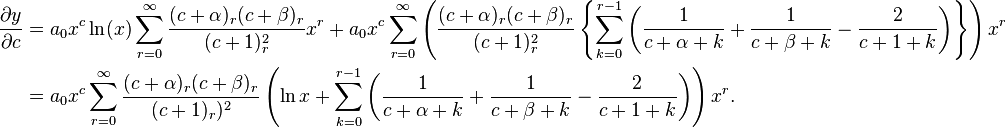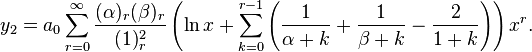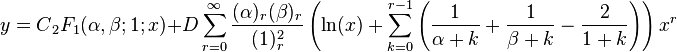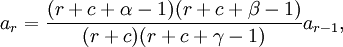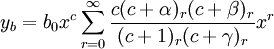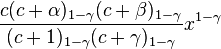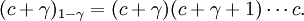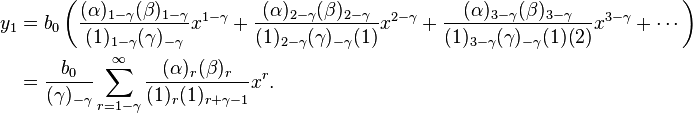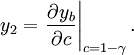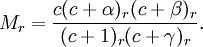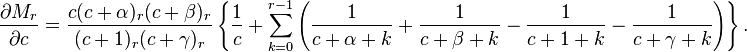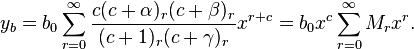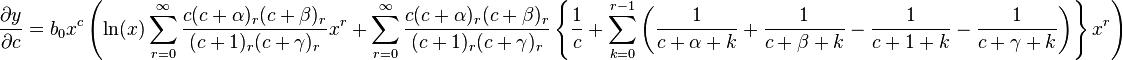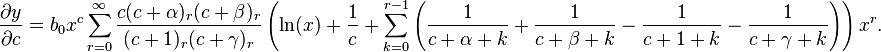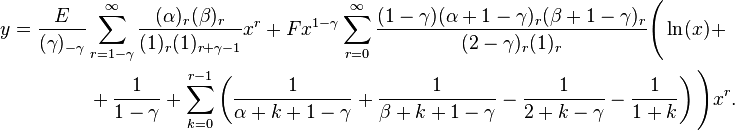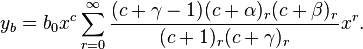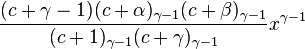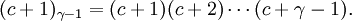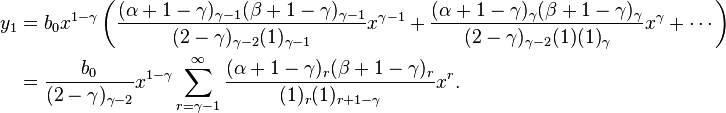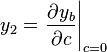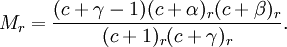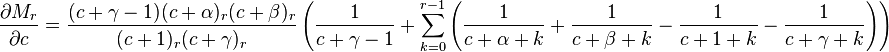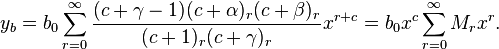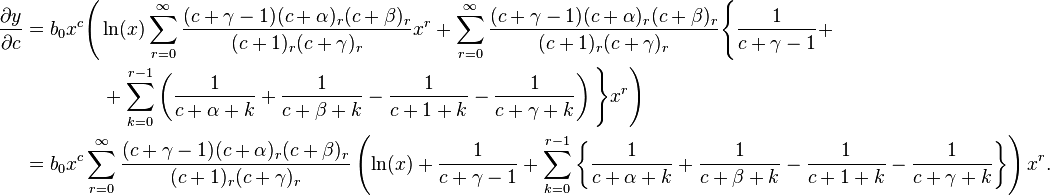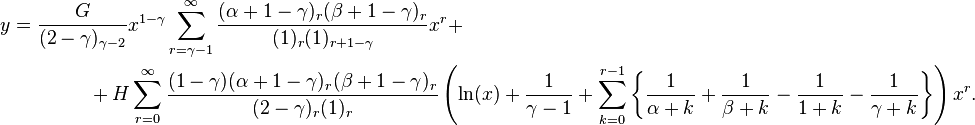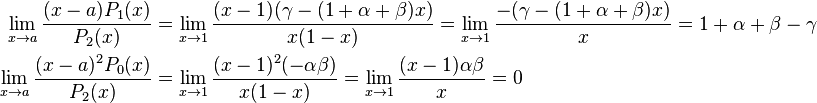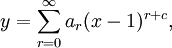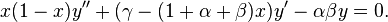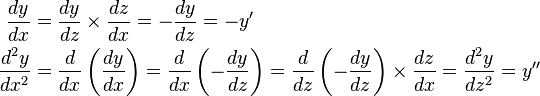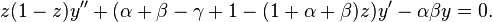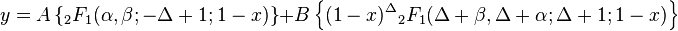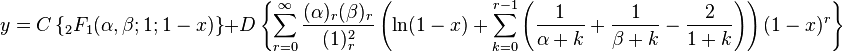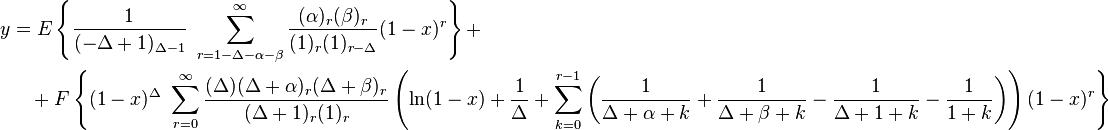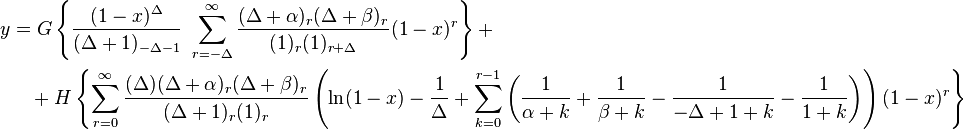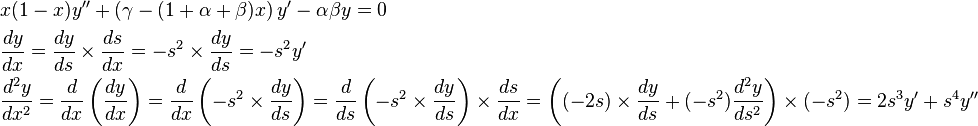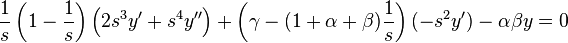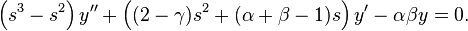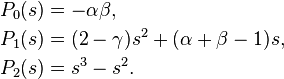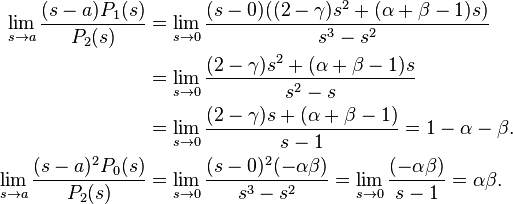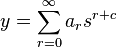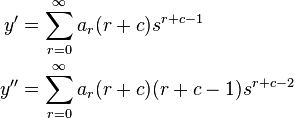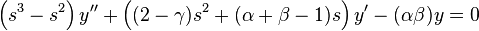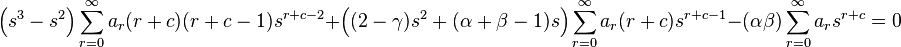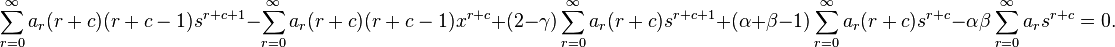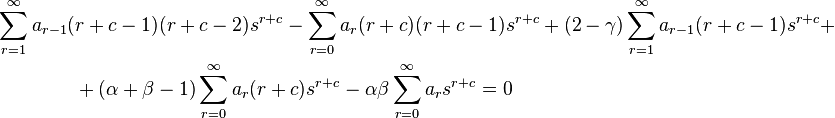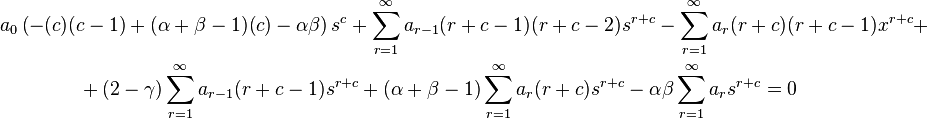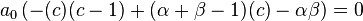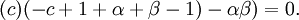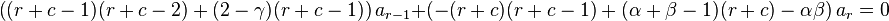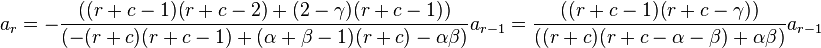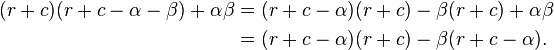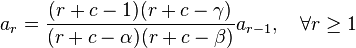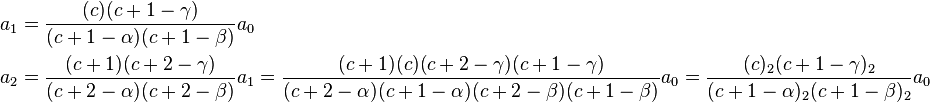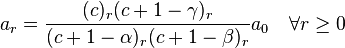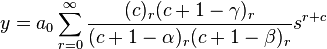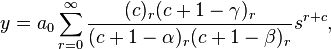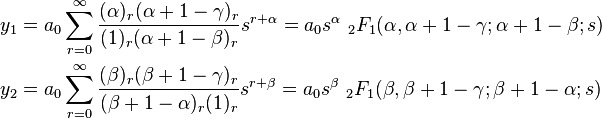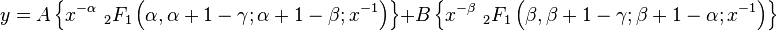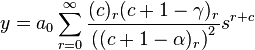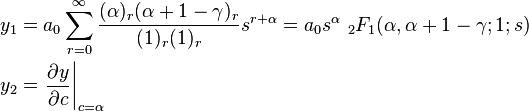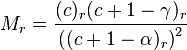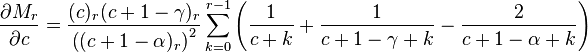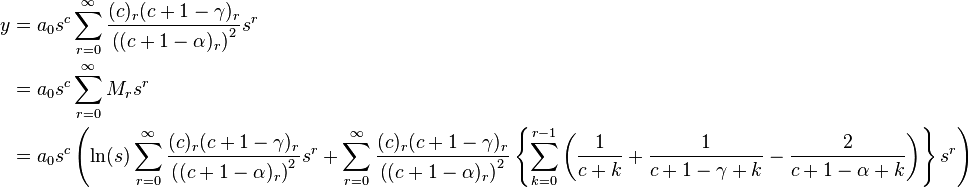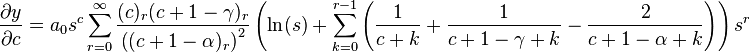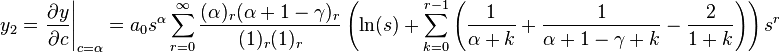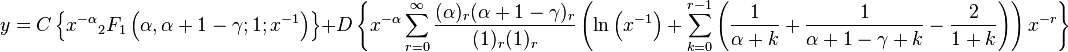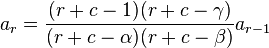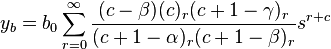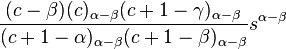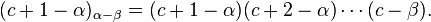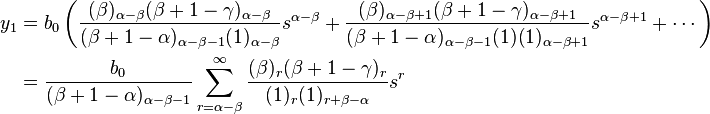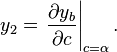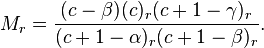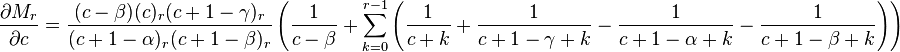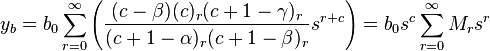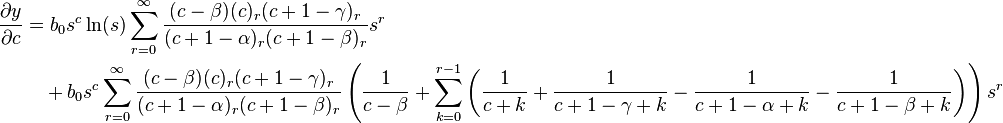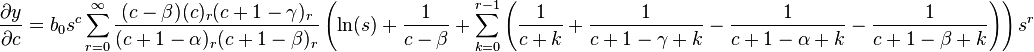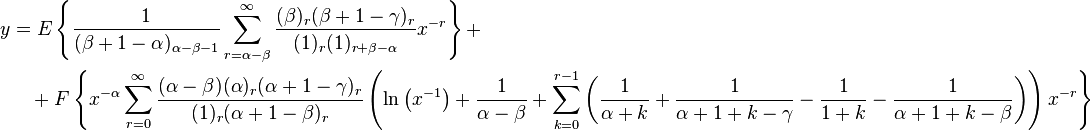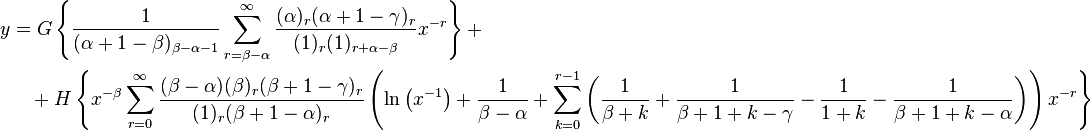Frobenius solution to the hypergeometric equation

In the following we solve the second-order differential equation called the hypergeometric differential equation using Frobenius method, named after Ferdinand Georg Frobenius. This is a method that uses the series solution for a differential equation, where we assume the solution takes the form of a series. This is usually the method we use for complicated ordinary differential equations.

The solution of the hypergeometric differential equation is very important. For instance, Legendre's differential equation can be shown to be a special case of the hypergeometric differential equation. Hence, by solving the hypergeometric differential equation, one may directly compare its solutions to get the solutions of Legendre's differential equation, after making the necessary substitutions. For more details, please check the hypergeometric differential equation.

We shall prove that this equation has three singularities, namely at x = 0, x = 1 and around x = infinity. However, as these will turn out to be regular singular points, we will be able to assume a solution on the form of a series. Since this is a second-order differential equation, we must have two linearly independent solutions.

The problem however will be that our assumed solutions may or not be independent, or worse, may not even be defined (depending on the value of the parameters of the equation). This is why we shall study the different cases for the parameters and modify our assumed solution accordingly.

The equation

Solve the hypergeometric equation around all singularities:

x(1-x)y''+\left\{ \gamma -(1+\alpha +\beta )x \right\}y'-\alpha \beta y=0

Solution around x = 0

Let

\begin{align} P_0(x) & = -\alpha \beta, \\ P_1(x) & = \gamma - (1+\alpha +\beta )x, \\ P_2(x) & = x(1-x) \end{align}

Then

P_2(0) = P_2 (1)=0.

Hence, x = 0 and x = 1 are singular points. Let's start with x = 0. To see if it is regular, we study the following limits:

\begin{align} \lim_{x \to a} \frac{(x - a) P_1(x)}{P_2(x)} &=\lim_{x \to 0} \frac{(x - 0)(\gamma - (1 + \alpha + \beta)x)}{x(1 - x)}=\lim_{x \to 0} \frac{x(\gamma - (1 + \alpha + \beta)x)}{x(1 - x)}= \gamma \\ \lim_{x \to a} \frac{(x - a)^2 P_0(x)}{P_2(x)} &= \lim_{x \to 0} \frac{(x - 0)^2(-\alpha \beta)}{x(1 - x)} = \lim_{x \to 0} \frac{x^2 (-\alpha \beta)}{x(1 - x)} = 0 \end{align}

Hence, both limits exist and x = 0 is a regular singular point. Therefore, we assume the solution takes the form

y = \sum_{r=0}^\infty a_r x^{r + c}

with a0 ≠ 0. Hence,

\begin{align} y' &= \sum_{r = 0}^\infty a_r(r + c) x^{r + c - 1} \\ y'' &= \sum_{r = 0}^\infty a_r(r + c)(r + c - 1) x^{r + c - 2}. \end{align}

Substituting these into the hypergeometric equation, we get

x \sum_{r = 0}^\infty a_r(r + c)(r + c - 1) x^{r + c - 2} - x^2 \sum_{r = 0}^\infty a_r(r + c)(r + c - 1) x^{r + c - 2} + \gamma \sum_{r = 0}^\infty a_r(r + c) x^{r + c - 1} - (1 + \alpha + \beta) x\sum_{r = 0}^\infty a_r(r + c) x^{r + c - 1} -\alpha \beta \sum_{r = 0}^\infty a_r x^{r + c} = 0

That is,

\sum_{r = 0}^\infty a_r(r + c)(r + c - 1) x^{r + c - 1} -\sum_{r = 0}^\infty a_r(r + c)(r + c - 1) x^{r + c}+\gamma \sum_{r = 0}^\infty a_r(r + c) x^{r + c - 1} -(1 + \alpha + \beta) \sum_{r = 0}^\infty a_r(r + c) x^{r + c} -\alpha \beta \sum_{r = 0}^\infty a_r x^{r + c} =0

In order to simplify this equation, we need all powers to be the same, equal to r + c − 1, the smallest power. Hence, we switch the indices as follows:

\begin{align} &\sum_{r = 0}^\infty a_r(r + c)(r + c - 1)x^{r + c - 1} -\sum_{r = 1}^\infty a_{r - 1}(r + c - 1)(r + c - 2) x^{r + c - 1} +\gamma \sum_{r = 0}^\infty a_r(r + c) x^{r + c - 1} \\ &\qquad -(1 + \alpha + \beta) \sum_{r = 1}^\infty a_{r - 1}(r + c - 1) x^{r + c - 1}-\alpha \beta \sum_{r = 1}^\infty a_{r - 1} x^{r + c - 1} =0 \end{align}

Thus, isolating the first term of the sums starting from 0 we get

\begin{align} &a_0 (c(c-1) + \gamma c) x^{c - 1}+ \sum_{r = 1}^\infty a_r(r + c)(r + c - 1) x^{r + c - 1} -\sum_{r = 1}^\infty a_{r - 1}(r + c - 1)(r + c - 2) x^{r + c - 1} \\ &\qquad + \gamma \sum_{r = 1}^\infty a_r(r + c) x^{r + c - 1}-(1 + \alpha + \beta) \sum_{r = 1}^\infty a_{r - 1}(r + c - 1) x^{r + c - 1}-\alpha \beta \sum_{r = 1}^\infty a_{r - 1} x^{r + c - 1}= 0 \end{align}

Now, from the linear independence of all powers of x, that is, of the functions 1, x, x2, etc., the coefficients of xk vanish for all k. Hence, from the first term, we have

a_{0} (c(c - 1) + \gamma c) = 0

which is the indicial equation. Since a0 ≠ 0, we have

c(c - 1 + \gamma) = 0.

Hence,

c_1 = 0, c_2 = 1 - \gamma

Also, from the rest of the terms, we have

((r + c)(r + c - 1) + \gamma(r+c)) a_r + (-(r + c - 1)(r + c - 2) - (1 + \alpha + \beta)(r + c - 1) - \alpha\beta) a_{r - 1}= 0

Hence,

\begin{align} a_r &= \frac{(r + c - 1)(r + c - 2) + (1 + \alpha + \beta)(r + c - 1) + \alpha\beta} {(r + c)(r + c - 1) + \gamma(r + c)} a_{r - 1} \\ &= \frac{(r + c -1)(r + c + \alpha + \beta - 1) + \alpha\beta}{(r + c)(r + c + \gamma - 1)} a_{r - 1} \end{align}

But

\begin{align} (r + c - 1)(r + c + \alpha + \beta - 1) + \alpha\beta &= (r + c - 1)(r + c + \alpha - 1) + (r + c - 1)\beta + \alpha\beta \\ &= (r + c - 1)(r + c + \alpha - 1) + \beta(r + c + \alpha - 1) \end{align}

Hence, we get the recurrence relation

a_r = \frac{(r + c + \alpha - 1)(r + c + \beta - 1)}{(r + c)(r + c + \gamma - 1)} a_{r - 1}, \text{ for } r \geq 1.

Let's now simplify this relation by giving ar in terms of a0 instead of ar−1. From the recurrence relation (note: below, expressions of the form (u)r refer to the Pochhammer symbol).

\begin{align} a_1 &= \frac{(c + \alpha)(c + \beta)}{(c + 1)(c + \gamma)} a_0 \\ a_2 &= \frac{(c + \alpha + 1)(c + \beta + 1)}{(c + 2)(c + \gamma + 1)} a_1 = \frac{(c + \alpha + 1)(c + \alpha)(c + \beta)(c + \beta + 1)}{(c + 2)(c + 1)(c + \gamma)(c + \gamma + 1)} a_0 = \frac{(c + \alpha)_2 (c + \beta)_2}{(c + 1)_2 (c + \gamma)_2} a_0 \\ a_3 &= \frac{(c + \alpha + 2)(c + \beta + 2)}{(c + 3)(c + \gamma + 2)} a_2 = \frac{(c + \alpha)_2 (c + \alpha + 2)(c + \beta )_2 (c + \beta + 2)}{(c + 1)_2 (c + 3)(c + \gamma)_2 (c + \gamma + 2)} a_0 = \frac{(c + \alpha)_3 (c + \beta)_3}{(c + 1)_3 (c + \gamma)_3} a_0 \end{align}

As we can see,

a_r =\frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r(c + \gamma)_r} a_0, \text{ for } r \geq 0

Hence, our assumed solution takes the form

y = a_0 \sum_{r = 0}^\infty \frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} x^{r + c}.

We are now ready to study the solutions corresponding to the different cases for c1 − c2 = γ − 1 (this reduces to studying the nature of the parameter γ: whether it is an integer or not).

Analysis of the solution in terms of the difference γ − 1 of the two roots

γ not an integer

Then y1 = y|c = 0 and y2 = y|c = 1 − γ. Since

y = a_0 \sum_{r = 0}^\infty \frac{(c + \alpha )_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} x^{r + c},

we have

\begin{align} y_1 &= a_0 \sum_{r = 0}^\infty \frac{(\alpha)_r (\beta)_r}{(1)_r (\gamma)_r} x^r = a_0 \cdot {{}_2 F_1}(\alpha, \beta; \gamma; x) \\ y_2 &= a_0 \sum_{r = 0}^\infty \frac{(\alpha + 1 - \gamma)_r (\beta + 1 - \gamma)_r}{(1 - \gamma + 1)_r (1 - \gamma + \gamma)_r} x^{r + 1 - \gamma} \\ &= a_0 x^{1 - \gamma} \sum_{r = 0}^\infty \frac{(\alpha + 1 - \gamma)_r (\beta + 1 - \gamma)_r}{(1)_r (2 - \gamma)_r} x^r \\ &= a_0 x^{1 - \gamma} {{}_2 F_1}(\alpha - \gamma + 1, \beta - \gamma + 1; 2 - \gamma; x) \end{align}

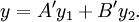Hence, y = A' y_1 + B' y_2. Let A′ a0 = a and B′ a0 = B. Then

y = A {{}_2 F_1}(\alpha, \beta; \gamma; x) + B x^{1 - \gamma} {{}_2 F_1}(\alpha - \gamma + 1, \beta - \gamma + 1; 2 - \gamma; x)\,

γ = 1

Then y1 = y|c = 0. Since γ = 1, we have

y = a_0 \sum_{r = 0}^\infty \frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r^2} x^{r + c}.

Hence,

\begin{align} y_1 &= a_0 \sum_{r = 0}^\infty \frac{(\alpha)_r (\beta)_r}{(1)_r (1)_r} x^r = a_0 {{}_2 F_1}(\alpha, \beta; 1; x) \\ y_2 &= \left.\frac{\partial y}{\partial c}\right|_{c = 0}. \end{align}

To calculate this derivative, let

M_r = \frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r^2}.

Then

\ln(M_r) = \ln\left(\frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r^2}\right)= \ln(c + \alpha)_r + \ln(c + \beta)_r - 2\ln(c + 1)_r

But

\ln(c + \alpha)_r = \ln\left((c + \alpha)(c + \alpha + 1) \cdots (c + \alpha + r - 1)\right) = \sum_{k = 0}^{r - 1} \ln(c + \alpha + k).

Hence,

\begin{align} \ln(M_r) &= \sum_{k = 0}^{r - 1} \ln(c + \alpha + k)+ \sum_{k = 0}^{r - 1} \ln(c + \beta + k)- 2 \sum_{k = 0}^{r - 1} \ln(c + 1 + k) \\ &= \sum_{k = 0}^{r - 1} \left(\ln(c + \alpha + k) + \ln(c + \beta + k) -2 \ln(c + 1 + k)\right) \end{align}

Differentiating both sides of the equation with respect to c, we get:

\frac{1}{M_r} \frac{\partial M_r}{\partial c}= \sum_{k = 0}^{r - 1} \left(\frac{1}{c + \alpha + k} + \frac{1}{c + \beta +k }- \frac{2}{c + 1 + k}\right).

Hence,

\frac{\partial M_r}{\partial c}= \frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r^2}\sum_{k=0}^{r-1} \left(\frac{1}{c + \alpha + k} + \frac{1}{c + \beta + k} - \frac{2}{c + 1 + k}\right).

Now,

y = a_0 x^c \sum_{r = 0}^\infty \frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r^2} x^r = a_0 x^c \sum_{r = 0}^\infty M_r x^r.

Hence,

\begin{align} \frac{\partial y}{\partial c} &= a_0 x^c \ln(x) \sum_{r = 0}^\infty \frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r^2} x^r + a_0 x^c \sum_{r = 0}^\infty \left(\frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r^2}\left\{\sum_{k = 0}^{r - 1} \left(\frac{1}{c + \alpha + k} + \frac{1}{c + \beta + k}- \frac{2}{c + 1 + k} \right) \right\} \right) x^r \\ &= a_0 x^c \sum_{r = 0}^\infty \frac{(c + \alpha)_r (c + \beta)_r}{(c + 1)_r)^2}\left(\ln x + \sum_{k = 0}^{r - 1} \left(\frac{1}{c + \alpha + k}+\frac{1}{c + \beta + k} - \frac{2}{c + 1 + k} \right) \right) x^r. \end{align}

For c = 0, we get

y_2 = a_0 \sum_{r=0}^\infty \frac{(\alpha)_r (\beta)_r}{(1)_r^2} \left(\ln x + \sum_{k = 0}^{r - 1} \left(\frac{1}{\alpha + k} + \frac{1}{\beta + k}-\frac{2}{1 + k} \right) \right) x^r.

Hence, y = C′y1 + D′y2. Let C′a0 = C and D′a0 = D. Then

y = C {{}_2 F_1}(\alpha, \beta; 1; x)+ D \sum_{r = 0}^\infty \frac{(\alpha)_r (\beta)_r}{(1)_r^2} \left(\ln(x) + \sum_{k = 0}^{r - 1} \left(\frac{1}{\alpha + k} + \frac{1}{\beta + k} - \frac{2}{1 + k} \right) \right) x^r

γ an integer and γ ≠ 1

γ ≤ 0

From the recurrence relation

a_r = \frac{(r + c + \alpha - 1)(r + c + \beta - 1)}{(r + c)(r + c + \gamma - 1)} a_{r - 1},

we see that when c = 0 (the smaller root), a1 − γ → ∞. Hence, we must make the substitution a0 = b0 (c - ci), where ci is the root for which our solution is infinite. Hence, we take a0 = b0 c and our assumed solution takes the new form

y_b = b_0 x^c \sum_{r = 0}^\infty \frac{c(c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} x^r

Then y1 = yb|c = 0. As we can see, all terms before

\frac{c(c + \alpha)_{1 - \gamma}(c + \beta)_{1 - \gamma}}{(c + 1)_{1 - \gamma}(c + \gamma)_{1 - \gamma}} x^{1 - \gamma}

vanish because of the c in the numerator. Starting from this term however, the c in the numerator vanishes. To see this, note that

(c + \gamma)_{1 - \gamma} = (c + \gamma)(c + \gamma + 1) \cdots c.

Hence, our solution takes the form

\begin{align} y_1 &= b_0 \left(\frac{(\alpha)_{1 - \gamma} (\beta)_{1 - \gamma}}{(1)_{1 - \gamma} (\gamma)_{-\gamma}} x^{1 - \gamma} + \frac{(\alpha)_{2 - \gamma} (\beta)_{2 - \gamma}}{(1)_{2 - \gamma} (\gamma)_{-\gamma}(1)} x^{2 - \gamma} + \frac{(\alpha)_{3 - \gamma} (\beta)_{3 - \gamma}}{(1)_{3 - \gamma} (\gamma)_{-\gamma}(1)(2)} x^{3 - \gamma} + \cdots \right) \\ &= \frac{b_0}{(\gamma)_{-\gamma}} \sum_{r = 1 - \gamma}^\infty \frac{(\alpha)_r (\beta)_r}{(1)_r (1)_{r + \gamma - 1}} x^r. \end{align}

Now,

y_2 = \left.\frac{\partial y_b}{\partial c}\right|_{c = 1 - \gamma}.

To calculate this derivative, let

M_r = \frac{c(c + \alpha)_r (c + \beta)_r}{(c + 1)_r(c + \gamma)_r}.

Then following the method in the previous case, we get

\frac{\partial M_r}{\partial c} = \frac{c(c + \alpha)_r (c + \beta )_r}{(c + 1)_r (c + \gamma)_r} \left\{\frac{1}{c} + \sum_{k = 0}^{r - 1} \left(\frac{1}{c + \alpha + k} + \frac{1}{c + \beta + k} - \frac{1}{c + 1 + k} -\frac{1}{c + \gamma + k} \right) \right\}.

Now,

y_b = b_0 \sum_{r = 0}^\infty \frac{c(c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} x^{r + c} = b_0 x^c \sum_{r = 0}^\infty M_r x^r.

Hence,

\begin{align} \frac{\partial y}{\partial c} &= b_0 x^c \left (\ln(x) \sum_{r = 0}^\infty \frac{c(c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} x^r +\sum_{r = 0}^\infty \frac{c(c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} \left\{\frac{1}{c} + \sum_{k = 0}^{r - 1} \left(\frac{1}{c + \alpha + k} + \frac{1}{c + \beta + k} - \frac{1}{c + 1 + k} - \frac{1}{c + \gamma + k} \right) \right\} x^r \right ) \end{align}

Hence,

\frac{\partial y}{\partial c} = b_0 x^c \sum_{r = 0}^\infty \frac{c(c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} \left(\ln(x) + \frac{1}{c} + \sum_{k = 0}^{r - 1} \left(\frac{1}{c + \alpha + k} + \frac{1}{c + \beta + k} - \frac{1}{c + 1 + k} - \frac{1}{c + \gamma + k} \right) \right) x^r.

At c = 1 − γ, we get y2. Hence, y = E′ y1 + F′ y2. Let E′ b0 = E and F′ b0 = F. Then

\begin{align} y &= \frac{E}{(\gamma)_{-\gamma}} \sum_{r = 1 - \gamma}^\infty \frac{(\alpha)_r (\beta)_r}{(1)_r (1)_{r + \gamma - 1}} x^r + F x^{1 - \gamma} \sum_{r = 0}^\infty \frac{(1 - \gamma) (\alpha + 1 - \gamma)_r (\beta + 1 - \gamma)_r}{(2 - \gamma)_r (1)_r}\Biggl(\ln(x) + \\ &\qquad \qquad + \frac{1}{1 - \gamma} + \sum_{k = 0}^{r - 1} \left(\frac{1}{\alpha + k + 1 - \gamma} + \frac{1}{\beta + k + 1 - \gamma}- \frac{1}{2 + k - \gamma} - \frac{1}{1 + k} \right) \Biggr) x^r. \end{align}

γ > 1

From the recurrence relation

a_r = \frac{(r + c + \alpha - 1)(r + c + \beta - 1)}{(r + c)(r + c + \gamma - 1)} a_{r - 1},

we see that when c = 1 - γ (the smaller root), aγ−1 → ∞. Hence, we must make the substitution a0 = b0(c − ci), where ci is the root for which our solution is infinite. Hence, we take a0 = b0(c + γ - 1) and our assumed solution takes the new form:

y_b = b_0 x^c \sum_{r = 0}^\infty \frac{(c + \gamma -1 )(c + \alpha )_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} x^r.

Then y1 = yb|c = 1 - γ. All terms before

\frac{(c + \gamma - 1)(c + \alpha)_{\gamma - 1} (c + \beta)_{\gamma - 1}}{(c + 1)_{\gamma - 1}(c + \gamma)_{\gamma - 1}} x^{\gamma - 1}

vanish because of the c + γ - 1 in the numerator. Starting from this term, however, the c + γ - 1 in the numerator vanishes. To see this, note that

(c + 1)_{\gamma - 1} = (c + 1)(c + 2)\cdots(c + \gamma - 1).

Hence, our solution takes the form

\begin{align} y_1 &= b_0 x^{1 - \gamma} \left(\frac{(\alpha + 1 - \gamma)_{\gamma - 1} (\beta + 1 - \gamma)_{\gamma - 1}}{(2 - \gamma)_{\gamma - 2} (1)_{\gamma - 1}} x^{\gamma - 1} + \frac{(\alpha + 1 - \gamma)_{\gamma} (\beta + 1 - \gamma)_{\gamma}}{(2 - \gamma)_{\gamma - 2} (1) (1)_{\gamma}} x^{\gamma}+ \cdots \right) \\ &= \frac{b_0}{(2 - \gamma)_{\gamma - 2}} x^{1 - \gamma}\sum_{r = \gamma - 1}^\infty \frac{(\alpha + 1 - \gamma)_r (\beta + 1 - \gamma)_r}{(1)_r (1)_{r + 1 - \gamma}} x^r. \end{align}

Now,

y_2 = \left.\frac{\partial y_b}{\partial c}\right|_{c = 0}

To calculate this derivative, let

M_r = \frac{(c + \gamma - 1)(c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r}.

Then following the method in the second case above,

\frac{\partial M_r}{\partial c} = \frac{(c + \gamma - 1) (c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} \left(\frac{1}{c + \gamma - 1} + \sum_{k = 0}^{r - 1} \left(\frac{1}{c + \alpha + k} + \frac{1}{c + \beta + k}- \frac{1}{c + 1 + k} - \frac{1}{c + \gamma + k} \right) \right)

Now,

y_b = b_0 \sum_{r = 0}^\infty \frac{(c + \gamma - 1) (c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} x^{r + c}= b_0 x^c \sum_{r = 0}^\infty M_r x^r.

Hence,

\begin{align} \frac{\partial y}{\partial c} &= b_0 x^c \Bigg ( \ln(x) \sum_{r = 0}^\infty \frac{(c + \gamma - 1) (c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r} x^r + \sum_{r = 0}^\infty \frac{(c + \gamma - 1) (c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r}\Bigg \{ \frac{1}{c + \gamma - 1} + \\ &\qquad \qquad+ \sum_{k = 0}^{r - 1} \left(\frac{1}{c + \alpha + k} + \frac{1}{c + \beta + k} - \frac{1}{c + 1 + k} - \frac{1}{c + \gamma + k} \right) \Bigg \} x^r \Bigg ) \\ &= b_0 x^c \sum_{r = 0}^\infty \frac{(c + \gamma - 1) (c + \alpha)_r (c + \beta)_r}{(c + 1)_r (c + \gamma)_r}\left(\ln(x) + \frac{1}{c + \gamma - 1} + \sum_{k = 0}^{r - 1} \left \{ \frac{1}{c + \alpha + k} + \frac{1}{c +\beta + k} - \frac{1}{c + 1 + k} - \frac{1}{c + \gamma + k} \right \} \right) x^r. \end{align}

At c = 0 we get y2. Hence, y = G′y1 + H′y2. Let G′b0 = E and H′b0 = F. Then

\begin{align} y &= \frac{G}{(2 - \gamma)_{\gamma - 2}} x^{1 - \gamma} \sum_{r=\gamma - 1}^\infty \frac{(\alpha + 1 - \gamma)_r (\beta + 1 - \gamma)_r}{(1)_r (1)_{r + 1 - \gamma}} x^r + \\ &\qquad \qquad+ H \sum_{r = 0}^\infty \frac{(1 - \gamma) (\alpha + 1 - \gamma)_r (\beta + 1 - \gamma)_r}{(2 - \gamma)_r (1)_r} \left(\ln(x) + \frac{1}{\gamma - 1} + \sum_{k = 0}^{r - 1} \left \{ \frac{1}{\alpha + k} + \frac{1}{\beta + k}- \frac{1}{1 + k} - \frac{1}{\gamma + k} \right \} \right) x^r. \end{align}

Solution around x = 1

Let us now study the singular point x = 1. To see if it is regular,

\begin{align} \lim_{x \to a} \frac{(x - a) P_1(x)}{P_2(x)} &= \lim_{x \to 1} \frac{(x - 1) (\gamma - (1 + \alpha + \beta)x)}{x(1 - x)} = \lim_{x \to 1} \frac{-(\gamma - (1 + \alpha + \beta)x)}{x} = 1 + \alpha + \beta - \gamma \\ \lim_{x \to a} \frac{(x - a)^2 P_0(x)}{P_2(x)} &= \lim_{x \to 1} \frac{(x - 1)^2 (-\alpha\beta)}{x(1 - x)} = \lim_{x \to 1} \frac{(x - 1) \alpha \beta}{x} = 0 \end{align}

Hence, both limits exist and x = 1 is a regular singular point. Now, instead of assuming a solution on the form

y = \sum_{r = 0}^\infty a_r (x - 1)^{r + c},

we will try to express the solutions of this case in terms of the solutions for the point x = 0. We proceed as follows: we had the hypergeometric equation

x(1 - x)y'' + (\gamma - (1 + \alpha + \beta)x)y' - \alpha\beta y = 0.

Let z = 1 − x. Then

\begin{align} \frac{dy}{dx} &= \frac{dy}{dz} \times \frac{dz}{dx} = -\frac{dy}{dz} = -y' \\ \frac{d^2 y}{dx^2} &= \frac{d}{dx}\left( \frac{dy}{dx} \right) = \frac{d}{dx}\left( -\frac{dy}{dz} \right) = \frac{d}{dz}\left( -\frac{dy}{dz} \right) \times \frac{dz}{dx} =\frac{d^{2}y}{dz^{2}} = y'' \end{align}

Hence, the equation takes the form

z(1 - z) y'' + (\alpha + \beta - \gamma + 1 - (1 + \alpha + \beta)z) y' - \alpha\beta y = 0.

Since z = 1 − x, the solution of the hypergeometric equation at x = 1 is the same as the solution for this equation at z = 0. But the solution at z = 0 is identical to the solution we obtained for the point x = 0, if we replace each γ by α + β − γ + 1. Hence, to get the solutions, we just make this substitution in the previous results. Note also that for x = 0, c1 = 0 and c2 = 1 − γ. Hence, in our case, c1 = 0 while c2 = γ − α − β. Let us now write the solutions. In the following we replaced each z by 1 - x.

Analysis of the solution in terms of the difference γ − α − β of the two roots

To simplify notation from now on denote γ − α − β by Δ, therefore γ = Δ + α + β.

Δ not an integer

y = A \left \{ {{}_2 F_1}(\alpha, \beta; -\Delta + 1; 1 - x) \right \} + B \left \{(1 - x)^{\Delta} {{}_2 F_1}(\Delta + \beta, \Delta + \alpha; \Delta + 1; 1 - x) \right \}

Δ = 0

y = C \left \{ {{}_2 F_1}(\alpha, \beta; 1; 1 - x) \right \} + D \left \{\sum_{r = 0}^\infty \frac{(\alpha)_r (\beta)_r}{(1)_r^2} \left(\ln(1 - x) + \sum_{k = 0}^{r - 1} \left(\frac{1}{\alpha + k} + \frac{1}{\beta + k} - \frac{2}{1 + k}\right)\right) (1 - x)^r \right \}

Δ is a non-zero integer

Δ > 0

\begin{align} y &= E \left \{ \frac{1}{(-\Delta + 1)_{\Delta - 1}} \ \sum_{r = 1 - \Delta - \alpha - \beta}^\infty \frac{(\alpha)_r (\beta)_r}{(1)_r (1)_{r - \Delta}} (1 - x)^r \right \} + \\ &\quad + F \left \{(1 - x)^{\Delta} \ \sum_{r = 0}^\infty \frac{(\Delta)(\Delta + \alpha)_r (\Delta + \beta)_r} {(\Delta + 1)_r (1)_r} \left (\ln(1 - x) + \frac{1}{\Delta} +\sum_{k=0}^{r-1} \left(\frac{1}{\Delta + \alpha + k} + \frac{1}{\Delta + \beta + k} - \frac{1}{\Delta + 1 + k} - \frac{1}{1 + k} \right) \right ) (1 - x)^r \right \} \end{align}

Δ < 0

\begin{align} y &= G \left \{ \frac{(1 - x)^{\Delta}}{(\Delta+1)_{-\Delta - 1}} \ \sum_{r = -\Delta}^\infty \frac{(\Delta + \alpha )_r (\Delta + \beta)_r}{(1)_r (1)_{r + \Delta}} (1 - x)^r \right \} + \\ &\quad + H \left \{ \sum_{r = 0}^\infty \frac{(\Delta)(\Delta + \alpha)_r (\Delta + \beta)_r}{(\Delta + 1)_r (1)_r}\left (\ln(1 - x) - \frac{1}{\Delta} + \sum_{k = 0}^{r - 1} \left(\frac{1}{\alpha + k} + \frac{1}{\beta + k} - \frac{1}{-\Delta + 1 + k} - \frac{1}{1 + k} \right)\right ) (1 - x)^r \right \} \end{align}

Solution around infinity

Finally, we study the singularity as x → ∞. Since we can't study this directly, we let x = s−1. Then the solution of the equation as x → ∞ is identical to the solution of the modified equation when s = 0. We had

\begin{align} & x(1-x)y''+\left ( \gamma -(1+\alpha +\beta )x \right ) y'-\alpha \beta y=0 \\ & \frac{dy}{dx}=\frac{dy}{ds}\times \frac{ds}{dx}=-s^2\times \frac{dy}{ds}=-s^2y' \\ & \frac{d^{2}y}{dx^{2}}=\frac{d}{dx}\left( \frac{dy}{dx} \right)=\frac{d}{dx}\left( -s^2 \times \frac{dy}{ds} \right)=\frac{d}{ds}\left( -s^2 \times \frac{dy}{ds} \right)\times \frac{ds}{dx} = \left( (-2s)\times \frac{dy}{ds}+(-s^{2})\frac{d^{2}y}{ds^{2}} \right) \times (-s^{2})=2s^{3}y'+s^{4}y'' \end{align}

Hence, the equation takes the new form

\frac{1}{s} \left(1 - \frac{1}{s}\right) \left(2 s^3 y' + s^4 y''\right) + \left(\gamma - (1 + \alpha + \beta)\frac{1}{s} \right) (-s^2 y') - \alpha \beta y = 0

which reduces to

\left (s^{3}-s^{2} \right )y''+ \left ((2-\gamma )s^2 +(\alpha +\beta -1)s\right )y'-\alpha \beta y = 0.

Let

\begin{align} P_{0}(s) &=-\alpha \beta, \\ P_{1}(s) &= (2-\gamma )s^2+(\alpha +\beta -1)s, \\ P_{2}(s) &= s^3-s^2. \end{align}

As we said, we shall only study the solution when s = 0. As we can see, this is a singular point since P2(0) = 0. To see if it is regular,

\begin{align} \lim_{s \to a} \frac{(s-a)P_1(s)}{P_2(s)} & =\lim_{s \to 0} \frac{(s-0)((2-\gamma )s^2+(\alpha +\beta -1)s)}{s^3-s^2} \\ &= \lim_{s \to 0} \frac{(2-\gamma )s^{2}+(\alpha +\beta -1)s}{s^2-s} \\ &= \lim_{s \to 0} \frac{(2-\gamma )s+(\alpha +\beta -1)}{s-1}=1-\alpha -\beta. \\ \lim_{s \to a} \frac{(s-a)^2 P_0(s)}{P_2(s)} &=\lim_{s \to 0} \frac{(s-0)^2( -\alpha \beta)}{s^3-s^2}=\lim_{s \to 0} \frac{( -\alpha \beta)}{s-1}=\alpha \beta. \end{align}

Hence, both limits exist and s = 0 is a regular singular point. Therefore, we assume the solution takes the form

y=\sum_{r=0}^{\infty }{a_{r}s^{r+c}}

with a0 ≠ 0. Hence,

\begin{align} y'&=\sum\limits_{r=0}^{\infty }{a_{r}(r+c)s^{r+c-1}}\\ y''&=\sum\limits_{r=0}^{\infty }{a_{r}(r+c)(r+c-1)s^{r+c-2}} \end{align}

Substituting in the modified hypergeometric equation we get

\left (s^3-s^2 \right )y''+ \left ((2-\gamma )s^2+(\alpha +\beta -1)s \right )y' - (\alpha \beta) y=0

And therefore:

\left (s^3 - s^2 \right ) \sum_{r=0}^{\infty }{a_{r}(r+c)(r+c-1)s^{r+c-2}} + \left ((2-\gamma )s^2+(\alpha +\beta -1)s \right ) \sum_{r=0}^{\infty }{a_{r}(r+c)s^{r+c-1}}-(\alpha \beta) \sum_{r=0}^{\infty }{a_{r}s^{r+c}}=0

i.e.,

\sum_{r=0}^{\infty }{a_{r}(r+c)(r+c-1)s^{r+c+1}}-\sum_{r=0}^{\infty }{a_{r}(r+c)(r+c-1)x^{r+c}} +(2-\gamma )\sum_{r=0}^{\infty }{a_{r}(r+c)s^{r+c+1}}+(\alpha +\beta -1)\sum_{r=0}^{\infty }{a_{r}(r+c)s^{r+c}}-\alpha \beta \sum_{r=0}^{\infty }{a_{r}s^{r+c}}=0.

In order to simplify this equation, we need all powers to be the same, equal to r + c, the smallest power. Hence, we switch the indices as follows

\begin{align} &\sum_{r=1}^{\infty }{a_{r-1}(r+c-1)(r+c-2)s^{r+c}}-\sum_{r=0}^{\infty }{a_{r}(r+c)(r+c-1)s^{r+c}} +(2-\gamma )\sum_{r=1}^{\infty }{a_{r-1}(r+c-1)s^{r+c}}+ \\ &\qquad \qquad + (\alpha +\beta -1)\sum_{r=0}^{\infty }{a_{r}(r+c)s^{r+c}}-\alpha \beta \sum_{r=0}^{\infty }{a_{r}s^{r+c}}=0 \end{align}

Thus, isolating the first term of the sums starting from 0 we get

\begin{align} & a_{0}\left ( -(c)(c-1)+(\alpha +\beta -1)(c)-\alpha \beta \right )s^{c}+\sum_{r=1}^{\infty }{a_{r-1}(r+c-1)(r+c-2)s^{r+c}} -\sum_{r=1}^{\infty }{a_{r}(r+c)(r+c-1)x^{r+c}}+\\ & \qquad \qquad + (2-\gamma )\sum_{r=1}^{\infty }{a_{r-1}(r+c-1)s^{r+c}} +(\alpha +\beta -1)\sum_{r=1}^{\infty }{a_{r}(r+c)s^{r+c}}-\alpha \beta \sum_{r=1}^{\infty }{a_{r}s^{r+c}}=0 \end{align}

Now, from the linear independence of all powers of s (i.e., of the functions 1, s, s2, ...), the coefficients of sk vanish for all k. Hence, from the first term we have

a_{0}\left ( -(c)(c-1)+(\alpha +\beta -1)(c)-\alpha \beta \right )=0

which is the indicial equation. Since a0 ≠ 0, we have

(c)(-c+1+\alpha +\beta -1)-\alpha \beta )=0.

Hence, c1 = α and c2 = β.

Also, from the rest of the terms we have

\left ((r+c-1)(r+c-2)+(2-\gamma )(r+c-1) \right ) a_{r-1} +\left ( -(r+c)(r+c-1)+(\alpha +\beta -1)(r+c)-\alpha \beta \right ) a_r=0

Hence,

a_{r}=-\frac{\left ( (r+c-1)(r+c-2)+(2-\gamma )(r+c-1) \right )}{\left ( -(r+c)(r+c-1)+(\alpha +\beta -1)(r+c)-\alpha \beta \right )}a_{r-1} =\frac{\left ((r+c-1)(r+c-\gamma ) \right )}{\left ( (r+c)(r+c-\alpha -\beta )+\alpha \beta \right )}a_{r-1}

But

\begin{align} (r+c)(r+c-\alpha -\beta )+\alpha \beta &=(r+c-\alpha )(r+c)-\beta (r+c)+\alpha \beta \\ &=(r+c-\alpha )(r+c)-\beta (r+c-\alpha ). \end{align}

Hence, we get the recurrence relation

a_{r}=\frac{(r+c-1)(r+c-\gamma )}{(r+c-\alpha )(r+c-\beta )}a_{r-1}, \quad \forall r \ge 1

Let's now simplify this relation by giving ar in terms of a0 instead of ar−1. From the recurrence relation,

\begin{align} a_1 &=\frac{(c)(c+1-\gamma )}{(c+1-\alpha )(c+1-\beta )}a_{0} \\ a_2 &=\frac{(c+1)(c+2-\gamma )}{(c+2-\alpha )(c+2-\beta )}a_{1}=\frac{(c+1)(c)(c+2-\gamma )(c+1-\gamma )}{(c+2-\alpha )(c+1-\alpha )(c+2-\beta )(c+1-\beta )}a_{0} = \frac{(c)_{2}(c+1-\gamma )_{2}}{(c+1-\alpha )_{2}(c+1-\beta )_{2}}a_{0} \end{align}

As we can see,

a_{r}=\frac{(c)_r(c+1-\gamma )_r}{(c+1-\alpha )_{r}(c+1-\beta )_{r}}a_{0}\quad \forall r \ge 0

Hence, our assumed solution takes the form

y=a_{0}\sum_{r=0}^{\infty} \frac{(c)_{r}(c+1-\gamma )_{r}}{(c+1-\alpha )_{r}(c+1-\beta )_{r}}s^{r+c}

We are now ready to study the solutions corresponding to the different cases for c1 − c2 = α − β.

Analysis of the solution in terms of the difference α − β of the two roots

α − β not an integer

Then y1 = y|c = α and y2 = y|c = β. Since

y=a_0 \sum_{r=0}^{\infty} \frac{(c)_{r}(c+1-\gamma )_{r}}{(c+1-\alpha )_{r}(c+1-\beta )_{r}}s^{r+c},

we have

\begin{align} y_1&=a_0 \sum_{r=0}^{\infty} \frac{(\alpha )_r (\alpha +1-\gamma )_r}{(1)_r (\alpha +1-\beta )_r} s^{r+\alpha} =a_0 s^{\alpha} \ {}_2F_1(\alpha, \alpha +1-\gamma ; \alpha +1-\beta ; s) \\ y_2&=a_0 \sum_{r=0}^{\infty} \frac{(\beta )_r (\beta +1-\gamma )_r}{(\beta +1-\alpha )_r (1)_r} s^{r+\beta} =a_0 s^{\beta} \ {}_2F_1(\beta, \beta +1-\gamma ; \beta +1-\alpha ;s) \end{align}

Hence, y = A′y1 + B′y2. Let A′a0 = A and B′a0 = B. Then, noting that s = x−1,

y=A \left \{ x^{-\alpha} \ {}_{2}F_{1} \left (\alpha, \alpha +1-\gamma ; \alpha +1-\beta ; x^{-1} \right ) \right \}+B \left \{ x^{-\beta} \ {}_{2}F_{1} \left (\beta, \beta +1-\gamma ; \beta +1-\alpha ; x^{-1} \right ) \right \}

α − β = 0

Then y1 = y|c = α. Since α = β, we have

y=a_{0}\sum_{r=0}^{\infty }{\frac{(c)_{r}(c+1-\gamma )_{r}}{\left( (c+1-\alpha )_{r} \right)^{2}}s^{r+c}}

Hence,

\begin{align} y_{1} &= a_{0}\sum_{r=0}^{\infty }{\frac{(\alpha )_{r}(\alpha +1-\gamma )_{r}}{(1)_{r}(1)_{r}}s^{r+\alpha } }=a_0 s^{\alpha} \ {}_{2}F_{1}(\alpha, \alpha +1-\gamma ; 1; s) \\ y_{2} &= \left. \frac{\partial y}{\partial c}\right |_{c=\alpha} \end{align}

To calculate this derivative, let

M_{r}=\frac{(c)_{r}(c+1-\gamma )_{r}}{\left( (c+1-\alpha )_{r} \right)^{2}}

Then using the method in the case γ = 1 above, we get

\frac{\partial M_r}{\partial c}=\frac{(c)_r(c+1-\gamma)_r}{\left( (c+1-\alpha )_{r} \right)^{2}} \sum_{k=0}^{r-1} \left( \frac{1}{c+k}+\frac{1}{c+1-\gamma +k}-\frac{2}{c+1-\alpha +k} \right)

Now,

\begin{align} y &=a_{0}s^{c}\sum_{r=0}^{\infty } \frac{(c)_{r}(c+1-\gamma )_r}{\left( (c+1-\alpha )_r \right)^{2}}s^r \\ &=a_{0}s^{c}\sum_{r=0}^{\infty }{M_{r}s^{r}} \\ &=a_0 s^c \left (\ln(s)\sum_{r=0}^{\infty} \frac{(c)_{r}(c+1-\gamma )_{r}}{\left( (c+1-\alpha )_r \right)^{2}}s^r + \sum_{r=0}^{\infty } \frac{(c)_{r}(c+1-\gamma )_{r}}{\left( (c+1-\alpha)_r \right)^2}\left\{\sum_{k=0}^{r-1}{\left( \frac{1}{c+k}+\frac{1}{c+1-\gamma +k}-\frac{2}{c+1-\alpha +k} \right)} \right\}s^r \right ) \end{align}

Hence,

\frac{\partial y}{\partial c}=a_{0}s^{c}\sum_{r=0}^{\infty } \frac{(c)_{r}(c+1-\gamma )_{r}}{\left( (c+1-\alpha )_{r} \right)^{2}} \left( \ln(s) + \sum_{k=0}^{r-1}{\left( \frac{1}{c+k}+\frac{1}{c+1-\gamma +k}-\frac{2}{c+1-\alpha +k} \right)} \right)s^r

Therefore:

y_2 = \left. \frac{\partial y}{\partial c}\right |_{c=\alpha} = a_0 s^{\alpha }\sum_{r=0}^{\infty } \frac{(\alpha )_{r}(\alpha +1-\gamma )_{r}}{(1)_r (1)_r}\left( \ln(s) +\sum_{k=0}^{r-1} \left( \frac{1}{\alpha +k}+\frac{1}{\alpha +1-\gamma +k}-\frac{2}{1+k} \right) \right)s^r

Hence, y = C′y1 + D′y2. Let C′a0 = C and D′a0 = D. Noting that s = x−1,

y=C \left \{ x^{-\alpha} {}_2F_1 \left (\alpha, \alpha +1-\gamma ; 1; x^{-1} \right ) \right \} +D \left \{ x^{-\alpha} \sum_{r=0}^{\infty} \frac{(\alpha )_{r}(\alpha +1-\gamma )_{r}}{(1)_{r} (1)_{r}} \left( \ln \left (x^{-1} \right )+\sum_{k=0}^{r-1} \left( \frac{1}{\alpha +k}+\frac{1}{\alpha +1-\gamma +k}-\frac{2}{1+k} \right) \right) x^{-r} \right \}

α − β an integer and α − β ≠ 0

α − β > 0

From the recurrence relation

a_{r}=\frac{(r+c-1)(r+c-\gamma )}{(r+c-\alpha )(r+c-\beta )}a_{r-1}

we see that when c = β (the smaller root), aα−β → ∞. Hence, we must make the substitution a0 = b0(c − ci), where ci is the root for which our solution is infinite. Hence, we take a0 = b0(c − β) and our assumed solution takes the new form

y_{b}=b_{0}\sum_{r=0}^{\infty} \frac{(c-\beta )(c)_{r}(c+1-\gamma )_{r}}{(c+1-\alpha )_{r}(c+1-\beta )_{r}}s^{r+c}

Then y1 = yb|c = β. As we can see, all terms before

\frac{(c-\beta )(c)_{\alpha -\beta }(c+1-\gamma )_{\alpha -\beta }}{(c+1-\alpha )_{\alpha -\beta }(c+1-\beta )_{\alpha -\beta }}s^{\alpha -\beta }

vanish because of the c − β in the numerator.

But starting from this term, the c − β in the numerator vanishes. To see this, note that

(c+1-\alpha )_{\alpha -\beta } =(c+1-\alpha )(c+2-\alpha )\cdots(c-\beta ).

Hence, our solution takes the form

\begin{align} y_{1} &=b_0 \left( \frac{(\beta )_{\alpha -\beta }(\beta +1-\gamma )_{\alpha -\beta }}{(\beta +1-\alpha )_{\alpha -\beta -1}(1)_{\alpha -\beta }}s^{\alpha -\beta }+\frac{(\beta )_{\alpha -\beta +1}(\beta +1-\gamma )_{\alpha -\beta +1}}{(\beta +1-\alpha )_{\alpha -\beta -1}(1)(1)_{\alpha -\beta +1}}s^{\alpha -\beta +1}+ \cdots \right) \\ &=\frac{b_0}{(\beta +1-\alpha )_{\alpha -\beta -1}}\sum_{r=\alpha -\beta }^{\infty} \frac{(\beta )_{r}(\beta +1-\gamma )_r }{(1)_r (1)_{r+\beta -\alpha }}s^r \end{align}

Now,

y_2=\left.\frac{\partial y_{b}}{\partial c}\right|_{c=\alpha}.

To calculate this derivative, let

M_{r}=\frac{(c-\beta )(c)_{r}(c+1-\gamma )_{r}}{(c+1-\alpha )_{r}(c+1-\beta )_{r}}.

Then using the method in the case γ = 1 above we get

\frac{\partial M_r}{\partial c} = \frac{(c - \beta)(c)_r (c + 1 - \gamma)_r}{(c + 1 - \alpha)_r (c +1-\beta)_r}\left (\frac{1}{c - \beta} + \sum_{k = 0}^{r-1} \left(\frac{1}{c + k} + \frac{1}{c + 1 - \gamma + k} -\frac{1}{c + 1 - \alpha + k} - \frac{1}{c + 1 - \beta + k} \right) \right )

Now,

y_b=b_0\sum_{r=0}^{\infty }{\left( \frac{(c-\beta )(c)_{r}(c+1-\gamma )_{r}}{(c+1-\alpha )_{r}(c+1-\beta )_{r}}s^{r+c} \right)}=b_{0}s^c\sum_{r=0}^{\infty }{M_{r}s^{r}}

Hence,

\begin{align} \frac{\partial y}{\partial c} &= b_0 s^c \ln(s) \sum_{r = 0}^\infty \frac{(c - \beta)(c)_r (c + 1 - \gamma)_r}{(c + 1 - \alpha)_r (c + 1 - \beta)_r} s^r \\ & \quad + b_0 s^c \sum_{r = 0}^\infty \frac{(c - \beta) (c)_r (c + 1 - \gamma)_r}{(c + 1 - \alpha)_r (c + 1 - \beta)_r} \left (\frac{1}{c - \beta} + \sum_{k = 0}^{r - 1} \left(\frac{1}{c + k} + \frac{1}{c + 1 - \gamma + k} - \frac{1}{c + 1 - \alpha + k}- \frac{1}{c + 1 - \beta + k} \right) \right) s^r \end{align}

Hence,

\frac{\partial y}{\partial c} = b_0 s^c \sum_{r = 0}^\infty \frac{(c - \beta)(c)_r (c + 1 - \gamma)_r}{(c + 1 - \alpha)_r (c + 1 - \beta)_r} \left (\ln(s) + \frac{1}{c - \beta } + \sum_{k = 0}^{r - 1} \left(\frac{1}{c + k} + \frac{1}{c + 1 - \gamma + k} - \frac{1}{c + 1 - \alpha + k} - \frac{1}{c + 1 - \beta + k}\right) \right ) s^{r}

At c = α we get y2. Hence, y = E′y1 + F′y2. Let E′b0 = E and F′b0 = F. Noting that s = x−1 we get

\begin{align} y &= E \left \{ \frac{1}{(\beta + 1 - \alpha)_{\alpha - \beta - 1}} \sum_{r = \alpha - \beta}^\infty \frac{(\beta)_r (\beta + 1 - \gamma)_r}{(1)_r (1)_{r + \beta - \alpha}} x^{-r} \right \} + \\ & \quad+ F \left \{ x^{-\alpha} \sum_{r = 0}^\infty \frac{(\alpha - \beta) (\alpha)_r (\alpha + 1 - \gamma)_r}{(1)_r (\alpha + 1 - \beta)_r} \left (\ln \left (x^{-1} \right ) + \frac{1}{\alpha -\beta } + \sum_{k = 0}^{r - 1} \left(\frac{1}{\alpha + k} + \frac{1}{\alpha + 1 + k - \gamma} -\frac{1}{1 + k}-\frac{1}{\alpha + 1 + k - \beta} \right) \right ) x^{-r} \right \} \end{align}

α − β < 0

From the symmetry of the situation here, we see that

\begin{align} y &= G \left \{ \frac{1}{(\alpha + 1 - \beta)_{\beta - \alpha - 1}} \sum_{r = \beta - \alpha}^\infty \frac{(\alpha)_r (\alpha + 1 - \gamma)_r}{(1)_r (1)_{r + \alpha - \beta}} x^{-r} \right \} + \\ & \quad + H \left \{ x^{-\beta} \sum_{r = 0}^\infty \frac{(\beta - \alpha) (\beta)_r (\beta + 1 - \gamma)_r}{(1)_r (\beta + 1 - \alpha)_r} \left (\ln \left (x^{-1} \right ) + \frac{1}{\beta - \alpha } + \sum_{k = 0}^{r - 1} \left(\frac{1}{\beta + k} + \frac{1}{\beta + 1 + k - \gamma} - \frac{1}{1 + k} - \frac{1}{\beta + 1 + k - \alpha} \right) \right ) x^{-r} \right \} \end{align}

References

This article is issued from Wikipedia - version of the Thursday, February 11, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.