Exciton
| Condensed matter physics |
|---|
 |
| Phases · Phase transition |
|
Phase phenomena |
|
Electronic phases |
|
Electronic phenomena |
|
Magnetic phases |
|
Scientists Van der Waals · Onnes · von Laue · Bragg · Debye · Bloch · Onsager · Mott · Peierls · Landau · Luttinger · Anderson · Van Vleck · Mott · Hubbard · Shockley · Bardeen · Cooper · Schrieffer · Josephson · Louis Néel · Esaki · Giaever · Kohn · Kadanoff · Fisher · Wilson · von Klitzing · Binnig · Rohrer · Bednorz · Müller · Laughlin · Störmer · Tsui · Abrikosov · Ginzburg · Leggett |
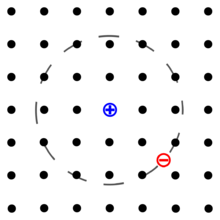
An exciton is a bound state of an electron and an electron hole which are attracted to each other by the electrostatic Coulomb force. It is an electrically neutral quasiparticle that exists in insulators, semiconductors and in some liquids. The exciton is regarded as an elementary excitation of condensed matter that can transport energy without transporting net electric charge.[1][2]
An exciton can form when a photon is absorbed by a semiconductor.[3] This excites an electron from the valence band into the conduction band. In turn, this leaves behind a positively charged electron hole (an abstraction for the location from which an electron was moved). The electron in the conduction band is then effectively attracted to this localized hole by the repulsive Coulomb forces from large numbers of electrons surrounding the hole and excited electron. This attraction provides a stabilizing energy balance. Consequently, the exciton has slightly less energy than the unbound electron and hole. The wavefunction of the bound state is said to be hydrogenic, an exotic atom state akin to that of a hydrogen atom. However, the binding energy is much smaller and the particle's size much larger than a hydrogen atom. This is because of both the screening of the Coulomb force by other electrons in the semiconductor (i.e., its dielectric constant), and the small effective masses of the excited electron and hole. The recombination of the electron and hole, i.e. the decay of the exciton, is limited by resonance stabilization due to the overlap of the electron and hole wave functions, resulting in an extended lifetime for the exciton.
The electron and hole may have either parallel or anti-parallel spins. The spins are coupled by the exchange interaction, giving rise to exciton fine structure. In periodic lattices, the properties of an exciton show momentum (k-vector) dependence.
The concept of excitons was first proposed by Yakov Frenkel in 1931,[4] when he described the excitation of atoms in a lattice of insulators. He proposed that this excited state would be able to travel in a particle-like fashion through the lattice without the net transfer of charge.
Classification
Excitons may be treated in two limiting cases, depending on the properties of the material in question.
Frenkel excitons
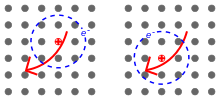
In materials with a small dielectric constant, the Coulomb interaction between an electron and a hole may be strong and the excitons thus tend to be small, of the same order as the size of the unit cell. Molecular excitons may even be entirely located on the same molecule, as in fullerenes. This Frenkel exciton, named after Yakov Frenkel, has a typical binding energy on the order of 0.1 to 1 eV. Frenkel excitons are typically found in alkali halide crystals and in organic molecular crystals composed of aromatic molecules, such as anthracene and tetracene.
Wannier-Mott excitons
In semiconductors, the dielectric constant is generally large. Consequently, electric field screening tends to reduce the Coulomb interaction between electrons and holes. The result is a Wannier exciton,[5] which has a radius larger than the lattice spacing. Small effective mass of electrons that is typical of semiconductors also favors large exciton radii. As a result, the effect of the lattice potential can be incorporated into the effective masses of the electron and hole. Likewise, because of the lower masses and the screened Coulomb interaction, the binding energy is usually much less than that of a hydrogen atom, typically on the order of 0.01eV. This type of exciton was named for Gregory Wannier and Nevill Francis Mott. Wannier-Mott excitons are typically found in semiconductor crystals with small energy gaps and high dielectric constants, but have also been identified in liquids, such as liquid xenon. They are also known as large excitons.
In single-wall carbon nanotubes, excitons have both Wannier-Mott and Frenkel character. This is due to the nature of the Coulomb interaction between electrons and holes in one-dimension. The dielectric function of the nanotube itself is large enough to allow for the spatial extent of the wave function to extend over a few to several nanometers along the tube axis, while poor screening in the vacuum or dielectric environment outside of the nanotube allows for large (0.4 to 1.0eV) binding energies.
Often there is more than one band to choose from for the electron and the hole leading to different types of excitons in the same material. Even high-lying bands can be effective as femtosecond two-photon experiments have shown. At cryogenic temperatures, many higher excitonic levels can be observed approaching the edge of the band,[6] forming a series of spectral absorption lines that are in principle similar to hydrogen spectral series.
Charge-transfer excitons
An intermediate case between Frenkel and Wannier excitons, charge-transfer excitons (sometimes called simply CT excitons) occur when the electron and the hole occupy adjacent molecules.[7] They occur primarily in ionic crystals.[8] Unlike Frenkel and Wannier excitons they display a static electric dipole moment.[9]
Surface excitons
At surfaces it is possible for so called image states to occur, where the hole is inside the solid and the electron is in the vacuum. These electron-hole pairs can only move along the surface.
Atomic and molecular excitons
Alternatively, an exciton may be an excited state of an atom, ion, or molecule, the excitation wandering from one cell of the lattice to another.
When a molecule absorbs a quantum of energy that corresponds to a transition from one molecular orbital to another molecular orbital, the resulting electronic excited state is also properly described as an exciton. An electron is said to be found in the lowest unoccupied orbital and an electron hole in the highest occupied molecular orbital, and since they are found within the same molecular orbital manifold, the electron-hole state is said to be bound. Molecular excitons typically have characteristic lifetimes on the order of nanoseconds, after which the ground electronic state is restored and the molecule undergoes photon or phonon emission. Molecular excitons have several interesting properties, one of which is energy transfer (see Förster resonance energy transfer) whereby if a molecular exciton has proper energetic matching to a second molecule's spectral absorbance, then an exciton may transfer (hop) from one molecule to another. The process is strongly dependent on intermolecular distance between the species in solution, and so the process has found application in sensing and molecular rulers.
The hallmark of molecular excitons in organic molecular crystals are doublets and/or triplets of exciton absorption bands strongly polarized along crystallographic axes. In these crystals an elementary cell includes several molecules sitting in symmetrically identical positions, which results in the level degeneracy that is lifted by intermolecular interaction. As a result, absorption bands are polarized along the symmetry axes of the crystal. Such multiplets were discovered by Antonina Prikhot'ko[10][11] and their genesis was proposed by Alexander Davydov. It is known as 'Davydov splitting'.[12][13]
Giant oscillator strength of bound excitons
Excitons are lowest excited states of the electronic subsystem of pure crystals. Impurities can bind excitons, and when the bound state is shallow, the oscillator strength for producing bound excitons is so high that impurity absorption can compete with intrinsic exciton absorption even at rather low impurity concentrations. This phenomenon is generic and applicable both to the large radius (Wannier-Mott) excitons and molecular (Frenkel) excitons. Hence, excitons bound to impurities and defects possess giant oscillator strength.[14]
Self-trapping of excitons
In crystals excitons interact with phonons, the lattice vibrations. If this coupling is weak as in typical semiconductors such as GaAs or Si, excitons are scattered by phonons. However, when the coupling is strong, excitons can be self-trapped.[15][16] Self-trapping results in dressing excitons with a dense cloud of virtual phonons which strongly suppresses the ability of excitons to move across the crystal. In simpler terms, this means a local deformation of the crystal lattice around the exciton. Self-trapping can be achieved only if the energy of this deformation can compete with the width of the exciton band. Hence, it should be of atomic scale, of about an electron-volt.
Self-trapping of excitons is similar to forming strong-coupling polarons but with three essential differences. First, self-trapped exciton states are always of a small radius, of the order of lattice constant, due to their electric neutrality. Second, there exists a self-trapping barrier separating free and self-trapped states, hence, free excitons are metastable. Third, this barrier enables coexistence of free and self-trapped states of excitons.[17][18] This means that spectral lines of free excitons and wide bands of self-trapped excitons can be seen simultaneously in absorption and luminescence spectra. It is interesting that while the self-trapped states are of lattice-spacing scale, the barrier has typically much larger scale. Indeed, its spacial scale is about 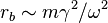 where
where  is effective mass of the exciton,
is effective mass of the exciton,  is the exciton-phonon coupling constant, and
is the exciton-phonon coupling constant, and 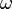 is the characteristic frequency of optical phonons. Excitons are self-trapped when
is the characteristic frequency of optical phonons. Excitons are self-trapped when  and
and  are large, and then the spacial size of the barrier is large compared with the lattice spacing. Transforming a free exciton state into a self-trapped one proceeds as a collective tunneling of coupled exciton-lattice system (an instanton). Because
are large, and then the spacial size of the barrier is large compared with the lattice spacing. Transforming a free exciton state into a self-trapped one proceeds as a collective tunneling of coupled exciton-lattice system (an instanton). Because 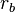 is large, tunneling can be described by a continuum theory.[19] The height of the barrier
is large, tunneling can be described by a continuum theory.[19] The height of the barrier 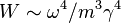 . Because both
. Because both  and
and  appear in the denominator of
appear in the denominator of 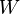 , the barriers are basically low. Therefore, free excitons can be seen in crystals with strong exciton-phonon coupling only in pure samples and at low temperatures. Coexistence of free and self-trapped excitons was observed in rare-gas solids,[20][21] alkali-halides,[22] and in molecular crystal of pyrene.[23]
, the barriers are basically low. Therefore, free excitons can be seen in crystals with strong exciton-phonon coupling only in pure samples and at low temperatures. Coexistence of free and self-trapped excitons was observed in rare-gas solids,[20][21] alkali-halides,[22] and in molecular crystal of pyrene.[23]
Interaction
Excitons are the main mechanism for light emission in semiconductors at low temperature (when the characteristic thermal energy kT is less than the exciton binding energy), replacing the free electron-hole recombination at higher temperatures.
The existence of exciton states may be inferred from the absorption of light associated with their excitation. Typically, excitons are observed just below the band gap.
When excitons interact with photons a so-called polariton (also exciton-polariton) is formed. These excitons are sometimes referred to as dressed excitons.
Provided the interaction is attractive, an exciton can bind with other excitons to form a biexciton, analogous to a dihydrogen molecule. If a large density of excitons is created in a material, they can interact with one another to form an electron-hole liquid, a state observed in k-space indirect semiconductors.
Additionally, excitons are integer-spin particles obeying Bose statistics in the low-density limit. In some systems, where the interactions are repulsive, a Bose–Einstein condensed state is predicted to be the ground state. Exciton condensates have been seen in a double quantum well systems.[24]
Spatially Direct and Indirect Excitons
Normally, excitons in a semiconductor have a very short lifetime due to the close proximity of the electron and hole. However, by placing the electron and hole in spatially separated quantum wells with an insulating barrier layer in between so called 'spatially indirect' excitons can be created. In contrast to ordinary (spatially direct), these spatially indirect excitons can have large spatial separation between the electron and hole, and thus possess a much longer lifetime. This is often used to cool excitons to very low temperatures in order to study Bose Einstein condensation (or rather its 2 dimensional analog).[25]
See also
References
- ↑ R. S. Knox, Theory of excitons, Solid state physics (Ed. by Seitz and Turnbul, Academic, NY), v. 5, 1963.
- ↑ Liang, W Y (1970). "Excitons". Physics Education 5 (125301). Bibcode:1970PhyEd...5..226L. doi:10.1088/0031-9120/5/4/003.
- ↑ Couto, ODD; Puebla, J (2011). "Charge control in InP/(Ga,In)P single quantum dots embedded in Schottky diodes". Physical Rev. B 84 (4): 226. Bibcode:1970PhyEd...5..226L. doi:10.1103/PhysRevB.84.125301.
- ↑ Frenkel, J. (1931). "On the Transformation of light into Heat in Solids. I". Physical Review 37: 17. Bibcode:1931PhRv...37...17F. doi:10.1103/PhysRev.37.17.
- ↑ Wannier, Gregory (1937). "The Structure of Electronic Excitation Levels in Insulating Crystals". Physical Review 52 (3): 191. Bibcode:1937PhRv...52..191W. doi:10.1103/PhysRev.52.191.
- ↑ http://www.nature.com/nature/journal/v514/n7522/full/nature13832.html
- ↑ J. D. Wright (1995) [First published 1987]. Molecular Crystals (2nd ed.). Cambridge University Press. p. 108. ISBN 0-521-47730-1.
- ↑ Ivan Pelant, Jan Valenta (2012). Luminescence Spectroscopy of Superconductors. Oxford University Press. p. 161. ISBN 978-0-19-958833-6.
- ↑ Guglielmo Lanzani (2012). The Photophysics Behind Photovoltaics and Photonics. Wiley-VCH Verlag. p. 82.
- ↑ A. Prikhotjko, Absorption Spectra of Crystals at Low Temperatures, J. Physics USSR 8, 257 (1944)
- ↑ A. F. Prikhot'ko, Izv, AN SSSR Ser. Fiz. 7, 499 (1948) http://ujp.bitp.kiev.ua/files/journals/53/si/53SI18p.pdf
- ↑ A.S Davydov, Theory of Molecular Excitons (Plenum, NY) 1971
- ↑ V. L. Broude, E. I. Rashba, and E. F. Sheka, Spectroscopy of molecular excitons (Springer, NY) 1985
- ↑ E. I. Rashba, Giant Oscillator Strengths Associated with Exciton Complexes, Sov. Phys. Semicond. 8, 807-816 (1975)
- ↑ N. Schwentner, E.-E. Koch, and J. Jortner, Electronic excitations in condensed rare gases, Springer tracts in modern physics, 107, 1 (1985).
- ↑ M. Ueta, H. Kanzaki, K. Kobayashi, Y. Toyozawa, and E. Hanamura. Excitonic Processes in Solids, Springer Series in Solid State Sciences, Vol. 60 (1986).
- ↑ E. I. Rashba, "Theory of Strong Interaction of Electron Excitations with Lattice Vibrations in Molecular Crystals, Optika i Spektroskopiya 2, 75, 88 (1957).
- ↑ E. I. Rashba, Self-trapping of excitons, in: Excitons (North-Holland, Amsterdam, 1982), p. 547.
- ↑ A. S. Ioselevich and E. I. Rashba, Theory of Nonradiative Trapping in Crystals, in: "Quantum tunneling in condensed media." Eds. Yu. Kagan and A. J. Leggett. (North-Holland, Amsterdam, 1992), p. 347-425.
- ↑ G. Zimmerer, "Excited-State Spectroscopy in Solids", in: Proceedings of the International School of Physics,``Enrico Fermi, Course XCVI, Varenna, Italy, 1985." (1987).
- ↑ I. Ya. Fugol', "Free and self-trapped excitons in cryocrystals: kinetics and relaxation processes." Advances in Physics 37, 1-35 (1988).
- ↑ Ch. B. Lushchik, in "Excitons," edited by E. I. Rashba, and M. D. Sturge, (North Holland, Amsterdam, 1982), p. 505.
- ↑ M. Furukawa, Ken-ichi Mizuno, A. Matsui, N. Tamai and I. Yamazaiu, Branching of Exciton Relaxation to the Free and Self-Trapped Exciton States, Chemical Physics 138, 423 (1989).
- ↑ "Exciton Condensation in Bilayer Quantum Hall Systems". Annual Review of Condensed Matter Physics. January 10, 2014. doi:10.1146/annurev-conmatphys-031113-133832.
- ↑ A. A. High (2012) "Spontaneous coherence in a cold exciton gas" Nature
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||