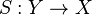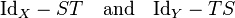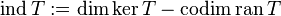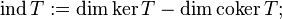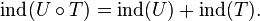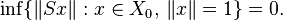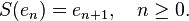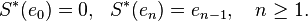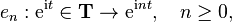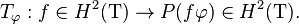Fredholm operator

Main article: Fredholm theory

In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm.

A Fredholm operator is a bounded linear operator between two Banach spaces, with finite-dimensional kernel and cokernel, and with closed range. (The last condition is actually redundant.^[1]) Equivalently, an operator T : X → Y is Fredholm if it is invertible modulo compact operators, i.e., if there exists a bounded linear operator

S: Y\to X

such that

\mathrm{Id}_X - ST \quad\text{and}\quad \mathrm{Id}_Y - TS

are compact operators on X and Y respectively.

The index of a Fredholm operator is

\mathrm{ind}\,T := \dim \ker T - \mathrm{codim}\,\mathrm{ran}\,T

or in other words,

\mathrm{ind}\,T := \dim \ker T - \mathrm{dim}\,\mathrm{coker}\,T;

see dimension, kernel, codimension, range, and cokernel.

Properties

The set of Fredholm operators from X to Y is open in the Banach space L(X, Y) of bounded linear operators, equipped with the operator norm. More precisely, when T₀ is Fredholm from X to Y, there exists ε > 0 such that every T in L(X, Y) with ||T − T₀|| < ε is Fredholm, with the same index as that of T₀.

When T is Fredholm from X to Y and U Fredholm from Y to Z, then the composition 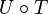$U \circ T$ is Fredholm from X to Z and

\mathrm{ind} (U \circ T) = \mathrm{ind}(U) + \mathrm{ind}(T).

When T is Fredholm, the transpose (or adjoint) operator T ′ is Fredholm from Y ′ to X ′, and ind(T ′) = −ind(T). When X and Y are Hilbert spaces, the same conclusion holds for the Hermitian adjoint T^∗.

When T is Fredholm and K a compact operator, then T + K is Fredholm. The index of T remains unchanged under compact perturbations of T. This follows from the fact that the index i(s) of T + s K is an integer defined for every s in [0, 1], and i(s) is locally constant, hence i(1) = i(0).

Invariance by perturbation is true for larger classes than the class of compact operators. For example, when T is Fredholm and S a strictly singular operator, then T + S is Fredholm with the same index.^[2] A bounded linear operator S from X to Y is strictly singular when its restriction to any infinite dimensional subspace X₀ of X fails to be an into isomorphism, that is:

\inf \{ \|S x\| : x \in X_0, \, \|x\| = 1 \} = 0. \,

Examples

Let H be a Hilbert space with an orthonormal basis {e_n} indexed by the non negative integers. The (right) shift operator S on H is defined by

S(e_n) = e_{n+1}, \quad n \ge 0. \,

This operator S is injective (actually, isometric) and has a closed range of codimension 1, hence S is Fredholm with ind(S) = −1. The powers S^k, k ≥ 0, are Fredholm with index −k. The adjoint S^∗ is the left shift,

S^*(e_0) = 0, \ \ S^*(e_n) = e_{n-1}, \quad n \ge 1. \,

The left shift S^∗ is Fredholm with index 1.

If H is the classical Hardy space H²(T) on the unit circle T in the complex plane, then the shift operator with respect to the orthonormal basis of complex exponentials

e_n : \mathrm{e}^{\mathrm{i} t} \in \mathbf{T} \rightarrow \mathrm{e}^{\mathrm{i} n t}, \quad n \ge 0, \,

is the multiplication operator M_φ with the function φ = e₁. More generally, let φ be a complex continuous function on T that does not vanish on T, and let T_φ denote the Toeplitz operator with symbol φ, equal to multiplication by φ followed by the orthogonal projection P from L²(T) onto H²(T):

T_\varphi : f \in H^2(\mathrm{T}) \rightarrow P(f \varphi) \in H^2(\mathrm{T}). \,

Then T_φ is a Fredholm operator on H²(T), with index related to the winding number around 0 of the closed path t ∈ [0, 2 π] → φ(e^i t) : the index of T_φ, as defined in this article, is the opposite of this winding number.

Applications

The Atiyah-Singer index theorem gives a topological characterization of the index of certain operators on manifolds.

An elliptic operator can be extended to a Fredholm operator. The use of Fredholm operators in partial differential equations is an abstract form of the parametrix method.

B-Fredholm operators

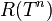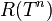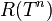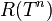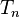For each integer $n$ , define $T_{n}$ to be the restriction of $T$ to $R(T^{n})$ viewed as a map from $R(T^{n})$ into $R(T^{n})$ ( in particular $T_{0} = T$ ). If for some integer $n$ the space $R(T^{n})$ is closed and $T_{n}$ is a Fredholm operator,then $T$ is called a B-Fredholm operator. The index of a B-Fredholm operator $T$ is defined as the index of the Fredholm operator $T_n$ . It is shown that the index is independent of the integer $n$ . B-Fredholm operators were introduced by M. Berkani in 1999 as a generalization of Fredholm operators.^[3]

Notes

The Wikibook Functional Analysis has a page on the topic of: Fredholm theory

↑ Yuri A. Abramovich and Charalambos D. Aliprantis, "An Invitation to Operator Theory", p.156
↑ T. Kato, "Perturbation theory for the nullity deficiency and other quantities of linear operators", J. d'Analyse Math. 6 (1958), 273–322.
↑ Berkani Mohammed: On a class of quasi-Fredholm operators. Integral Equations and Operator Theory, 34, 2 (1999), 244-249

References

D.E. Edmunds and W.D. Evans (1987), Spectral theory and differential operators, Oxford University Press. ISBN 0-19-853542-2.
A. G. Ramm, "A Simple Proof of the Fredholm Alternative and a Characterization of the Fredholm Operators", American Mathematical Monthly, 108 (2001) p. 855 (NB: In this paper the word "Fredholm operator" refers to "Fredholm operator of index 0").
Fredholm operator at PlanetMath.org.
Weisstein, Eric W., "Fredholm's Theorem", MathWorld.
B.V. Khvedelidze (2001), "Fredholm theorems", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Bruce K. Driver, "Compact and Fredholm Operators and the Spectral Theorem", Analysis Tools with Applications, Chapter 35, pp. 579–600.
Robert C. McOwen, "Fredholm theory of partial differential equations on complete Riemannian manifolds", Pacific J. Math. 87, no. 1 (1980), 169–185.
Tomasz Mrowka, A Brief Introduction to Linear Analysis: Fredholm Operators, Geometry of Manifolds, Fall 2004 (Massachusetts Institute of Technology: MIT OpenCouseWare)

Functional analysis

Set / subset types	Absolutely convex Absorbing Balanced Bounded Convex Radial Star-shaped Symmetric Linear cone (subset) Convex cone (subset)

TVS types	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (tame) Hilbert LF-space Locally convex Mackey Montel Nuclear Normed (norm) Quasinormed Reflexive Riesz Smith Stereotype Webbed Topological tensor product (of Hilbert spaces)

Mapping topologies	Dual Dual space Operator Strong (polar operator) Ultrastrong Weak (operator) Ultraweak Uniform convergence

Linear operators	Adjoint Bilinear (form) Bounded / Unbounded Closed Continuous / Discontinuous Compact Fredholm Hilbert–Schmidt Functionals (positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Set operations	Algebraic interior (core) Interior Minkowski addition Polar

Banach algebras	C-algebras Spectrum (C-algebra radius) Spectral theory

Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (hyperplane separation) Kakutani fixed-point Lomonosov's invariant subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Differentiation in Fréchet spaces Derivatives (Fréchet Gâteaux functional holomorphic) Integrals (Bochner Dunford Gelfand–Pettis regulated weak) Functional calculus (Borel continuous holomorphic) Inverse function theorem (Nash–Moser theorem) Vector measure

This article is issued from Wikipedia - version of the Thursday, January 21, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.