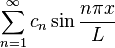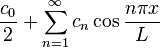Fourier sine and cosine series

In mathematics, particularly the field of calculus and Fourier analysis, the Fourier sine and cosine series are two mathematical series named after Joseph Fourier.

Notation

In this article, f denotes a real valued function on $[0,L]$ .

Sine series

The Fourier sine series of f is defined to be

\sum_{n=1}^\infty c_n \sin \frac{n\pi x}{L}

where

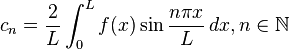c_n=\frac{2}{L}\int_0^L f(x) \sin \frac{n\pi x}{L} \, dx, n\in \mathbb{N}

If f is continuous and $f(0)=f(L)=0$ , then the Fourier sine series of f is equal to f on $[0,L]$ , odd, and periodic with period $2L$ .

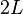Cosine series

The Fourier cosine series is defined to be

\frac{c_0}{2} + \sum_{n=1}^\infty c_n \cos \frac{n\pi x}{L}

where

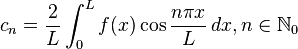c_n=\frac{2}{L}\int_0^L f(x) \cos \frac{n\pi x}{L} \, dx, n\in \mathbb{N}_0

If f is continuous, then the Fourier cosine series of f is equal to f on $[0,L]$ , even, and periodic with period $2L$ .

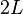Remarks

This notion can be generalized to functions which are not continuous.

References

Haberman, Richard. Applied Partial Differential Equations with Fourier Series and Boundary Value Problems (4th ed.). Pearson. pp. 97–113. ISBN 978-0130652430.

This article is issued from Wikipedia - version of the Thursday, October 16, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.