Four factor formula

The four-factor formula, also known as Fermi's four factor formula is used in nuclear engineering to determine the multiplication of a nuclear chain reaction in an infinite medium. The formula is[1]

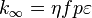
k_{\infty} = \eta f p \varepsilon
Symbol Name Meaning Formula
\eta Reproduction Factor (Eta)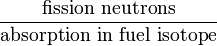
\frac{\mbox{fission neutrons}}{\mbox{absorption in fuel isotope}}
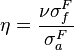 \eta = \frac{\nu \sigma_f^F}{\sigma_a^F}
f The thermal utilization factor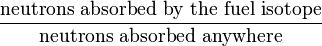
\frac{\mbox{neutrons absorbed by the fuel isotope}}{\mbox{neutrons absorbed anywhere}}
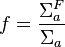 f = \frac{\Sigma_a^F}{\Sigma_a}
p The resonance escape probability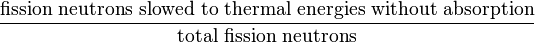
\frac{\mbox{fission neutrons slowed to thermal energies without absorption}}{\mbox{total fission neutrons}}
 p \approx \mathrm{exp} \left( -\frac{\sum\limits_{i=1}^{N} N_i I_{r,A,i}}{\left( \overline{\xi} \Sigma_p \right)_{mod}} \right)
\epsilon The fast fission factor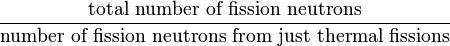
\frac{\mbox{total number of fission neutrons}}{\mbox{number of fission neutrons from just thermal fissions}}
 \varepsilon \approx 1 + \frac{1-p}{p}\frac{u_f \nu_f P_{FAF}}{f \nu_t P_{TAF} P_{TNL}}

The six factor formula defines each of these terms in much more detail.

Multiplication

The multiplication factor, k, is defined as (see Nuclear chain reaction):

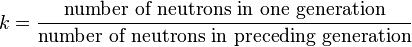
k = \frac{\mbox{number of neutrons in one generation}}{\mbox{number of neutrons in preceding generation}}

If k is greater than 1, the chain reaction is supercritical, and the neutron population will grow exponentially.
If k is less than 1, the chain reaction is subcritical, and the neutron population will exponentially decay.
If k = 1, the chain reaction is critical and the neutron population will remain constant.

In an infinite medium, neutrons cannot leak out of the system and the multiplication factor becomes the infinite multiplication factor, 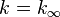k = k_{\infty}, which is approximated by the four-factor formula.

See also

References

  1. ↑ Duderstadt, James; Hamilton, Louis (1976). Nuclear Reactor Analysis. John Wiley & Sons, Inc. ISBN 0-471-22363-8.
This article is issued from Wikipedia - version of the Wednesday, September 09, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.