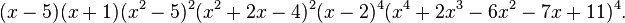Foster cage
| Foster cage | |
|---|---|
| Named after | Ronald Martin Foster |
| Vertices | 30 |
| Edges | 75 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 5 |
| Automorphisms | 30 |
| Chromatic number | 4 |
| Chromatic index | 5 |
| Properties | Cage |
In the mathematical field of graph theory, the Foster cage is a 5-regular undirected graph with 30 vertices and 75 edges.[1][2] It is one of the four (5,5)-cage graphs, the others being the Meringer graph, the Robertson–Wegner graph, and the Wong graph.
Like the unrelated Foster graph, it is named after R. M. Foster.
It has chromatic number 4, diameter 3, and is 5-vertex-connected.
Algebraic properties
The characteristic polynomial of the Foster cage is
References
- ↑ Weisstein, Eric W., "Foster Cage", MathWorld.
- ↑ Meringer, Markus (1999), "Fast generation of regular graphs and construction of cages", Journal of Graph Theory 30 (2): 137–146, doi:10.1002/(SICI)1097-0118(199902)30:2<137::AID-JGT7>3.0.CO;2-G, MR 1665972.
This article is issued from Wikipedia - version of the Friday, January 29, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.