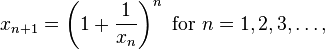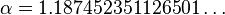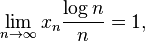Foias constant

In mathematical analysis, the Foias constant, is a number named after Ciprian Foias.

If x1 > 0 and

x_{n+1} = \left( 1 + \frac{1}{x_n} \right)^n\text{ for }n=1,2,3,\ldots,

then the Foias constant is the unique real number α such that if x1 = α then the sequence diverges to ∞.[1] Numerically, it is

\alpha = 1.187452351126501\ldots\,  A085848.

No closed form is known.

When x1 = α then we have the limit:

\lim_{n\to\infty} x_n \frac{\log n}n = 1,

where "log" denotes the usual natural logarithm.

A fortuitous observation between the prime number theorem and this constant goes as follows,

\lim_{n\to\infty} \frac{x_n}{\pi(n)} = 1,

where π is the prime-counting function.[2]

See also

Notes and references

  1. ↑ Ewing, J. and Foias, C. "An Interesting Serendipitous Real Number." In Finite versus Infinite: Contributions to an Eternal Dilemma (Ed. C. Caluse and G. Păun). London: Springer-Verlag, pp. 119–126, 2000.
  2. ↑ Ewing, J. and Foias, C. "An Interesting Serendipitous Real Number." In Finite versus Infinite: Contributions to an Eternal Dilemma (Ed. C. Caluse and G. Păun). London: Springer-Verlag, pp. 119–126, 2000.
This article is issued from Wikipedia - version of the Wednesday, March 19, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.