Fluorescence-lifetime imaging microscopy

Fluorescence-lifetime imaging microscopy or FLIM is an imaging technique for producing an image based on the differences in the exponential decay rate of the fluorescence from a fluorescent sample. It can be used as an imaging technique in confocal microscopy, two-photon excitation microscopy, and multiphoton tomography.

The lifetime of the fluorophore signal, rather than its intensity, is used to create the image in FLIM. This has the advantage of minimizing the effect of photon scattering in thick layers of sample.

Fluorescence lifetimes

A fluorophore which is excited by a photon will drop to the ground state with a certain probability based on the decay rates through a number of different (radiative and/or nonradiative) decay pathways. To observe fluorescence, one of these pathways must be by spontaneous emission of a photon. In the ensemble description, the fluorescence emitted will decay with time according to

I(t) = I_0 e^{-t/\tau}

where

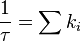\frac{1}{\tau} = \sum k_i.

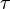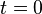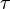In the above, t is time, \tau is the fluorescence lifetime, I_0 is the initial fluorescence at t=0, and k_i are the rates for each decay pathway, at least one of which must be the fluorescence decay rate k_f. More importantly, the lifetime, \tau is independent of the initial intensity and of the emitted light. This can be utilized for making non-intensity based measurements in chemical sensing.[1]

Measurement

Fluorescence-lifetime imaging yields images with the intensity of each pixel determined by 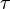\tau, which allows one to view contrast between materials with different fluorescence decay rates (even if those materials fluoresce at exactly the same wavelength), and also produces images which show changes in other decay pathways, such as in FRET imaging.

Pulsed illumination

Fluorescence lifetimes can be determined in the time domain by using a pulsed source. When a population of fluorophores is excited by an ultrashort or delta pulse of light, the time-resolved fluorescence will decay exponentially as described above. However, if the excitation pulse or detection response is wide, the measured fluorescence, d(t), will not be purely exponential. The instrumental response function, IRF(t) will be convolved or blended with the decay function, F(t).

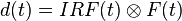
{d}(t) = {IRF}(t) \otimes {F}(t)

The instrumental response of the source, detector, and electronics can be measured, usually from scattered excitation light. Recovering the decay function (and corresponding lifetimes) poses additional challenges as division in the frequency domain tends to produce high noise when the denominator is close to zero.

TCSPC

Time-correlated single-photon counting (TCSPC) is usually employed because variations in source intensity and photoelectron amplitudes are ignored, the time resolution can be upwards of 4 ps, and the data obeys Poisson statistics (useful in determining goodness of fit during reconvolution). More specifically, TCSPC records times at which individual photons are detected by something like a photo-multiplier tube (PMT) or an avalanche photo diode (APD) after a single pulse. The recordings are repeated for additional pulses and after enough recorded events, one is able to build a histogram of the number of events across all of these recorded time points. This histogram can then be fit to an exponential function that contains the exponential lifetime decay function of interest, and the lifetime parameter can accordingly be extracted. 16~64 multichannel PMT systems have been commercially available, whereas the recently demonstrated CMOS single-photon avalanche diode (SPAD)-TCSPC FLIM systems can offer additional low-cost options.[2]

Gating method

Pulse excitation is still used in this method. Before the pulse reaches the sample, some of the light is reflected by a dichroic mirror and gets detected by a photodiode that activates a delay generator controlling a gated optical intensifier (GOI) that sits in front of the CCD detector. The GOI only allows for detection for the fraction of time when it is open after the delay. Thus, with an adjustable delay generator, one is able to collect fluorescence emission after multiple delay times encompassing the time range of the fluorescence decay of the sample.[3][4] In recent years integrated intensified CCD cameras entered the market. These cameras consist of an image intensifier, CCD sensor and an integrated delay generator. ICCD cameras with shortest gating times of down to 200ps and delay steps of 10ps allow sub-nanosecond resolution FLIM. In combination with an endoscope this technique is used for intraoperative diagnosis of brain tumors.[5]

Phase modulation

Fluorescence lifetimes can be determined in the frequency domain by a phase-modulation method. The method uses a light source that is pulsed or modulated at high frequency (up to 500 MHz) such as an LED, diode laser or a continuous wave source combined with an electro-optic modulator or an acousto-optic modulator. The fluorescence is (a.) demodulated and (b.) phase shifted; both quantities are related to the characteristic decay times of the fluorophore. Also, y-components to the excitation and fluorescence sine waves will be modulated, and lifetime can be determined from the modulation ratio of these y-components. Hence, 2 values for the lifetime can be determined from the phase-modulation method. The lifetimes are determined through a fitting procedures of these experimental parameters. An advantage of PMT-based or camera-based frequency domain FLIM is its fast lifetime image acquisition making it suitable for applications such as live cell research.[6]

Analysis

The goal of the analysis algorithm is to extract the pure decay curve from the measured decay and to estimate the lifetime(s). The latter is usually accomplished by fitting single or multi exponential functions. A variety of methods have been developed to solve this problem. The most widely used technique is the least square iterative re-convolution which is based on the minimization of the weighted sum of the residuals. In this technique theoretical exponential decay curves are convoluted with the instrument response function, which is measured separately, and the best fit is found by iterative calculation of the residuals for different inputs until a minimum is found. For a set of observations 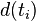d({{t}_{i}}) of the fluorescence signal in time bin i, the lifetime estimation is carried out by minimization of:

{{\chi }^{2}}=\sum\limits_{i}{{{\left[ {{d}_{i}}({{t}_{i}})-{{d}_{0i}}({{t}_{i}},a,\tau ) \right]}^{2}}}

Besides experimental difficulties, including the wavelength dependent instrument response function, mathematical treatment of the iterative de-convolution problem is not straight forward and it is a slow process which in the early days of FLIM made it impractical for a pixel-by-pixel analysis. Non fitting methods are attractive because they offer a very fast solution to lifetime estimation. One of the major and straightforward techniques in this category is the rapid lifetime determination (RLD) method. RLD calculates the lifetimes and their amplitudes directly by dividing the decay curve into two parts of equal width 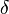\deltat. The analysis is performed by integrating the decay curve in equal time intervals 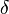\deltat:

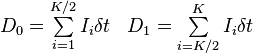
\begin{matrix} {{D}_{0}}=\sum\limits_{i=1}^{K/2}{{{I}_{i}}\delta t} & {{D}_{1}}=\sum\limits_{i=K/2}^{K}{{{I}_{i}}\delta t} \\ \end{matrix}

Ii is the recorded signal in the i-th channel and K is the number of channels. The lifetime can be estimated using:

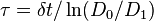
\tau =\delta t/\ln ({{D}_{0}}/{{D}_{1}})

For multi exponential decays this equation provides the average lifetime. This method can be extended to analyze bi-exponential decays. One major drawback of this method is that it cannot take into account the instrument response effect and for this reason the early part of the measured decay curves should be ignored in the analyses. This means that part of the signal is discarded and the accuracy for estimating short lifetimes goes down.

One of the interesting features of the convolution theorem is that the integral of the convolution is the product of the factors that make up the integral. There are a few techniques which work in transformed space that exploit this property to recover the pure decay curve from the measured curve. Laplace and Fourier transformation along with Laguerre gauss expansion have been used to estimate the lifetime in transformed space. These approaches are faster than the deconvolution based methods but they suffer from truncation and sampling problems. Moreover, application of methods like Laguerre gauss expansion is mathematically complicated. In Fourier methods the lifetime of a single exponential decay curve is given by:

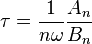
\tau =\frac{1}{n\omega }\frac{{{A}_{n}}}{{{B}_{n}}}

Where:

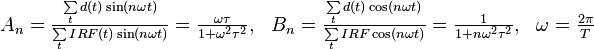
\begin{matrix} {{A}_{n}}=\frac{\sum\limits_{t}{d(t)\sin (n\omega t)}}{\sum\limits_{t}{IRF(t)\sin (n\omega t)}}=\frac{\omega \tau }{1+{{\omega }^{2}}{{\tau }^{2}}}, & {{B}_{n}}=\frac{\sum\limits_{t}{d(t)\cos (n\omega t)}}{\sum\limits_{t}{IRF\cos (n\omega t)}}=\frac{1}{1+n{{\omega }^{2}}{{\tau }^{2}}}, & \omega =\frac{2\pi }{T} \\ \end{matrix}

and n is the harmonic number and T is the total time range of detection.

Applications

FLIM has primarily been used in biology as a method to detect photosensitizers in cells and tumors as well as FRET in instances where ratiometric imaging is difficult. The technique was developed in the late 1980s and early 1990s (Gating method: Bugiel et al. 1989. König 1989,[7] Phase modulation: Lakowicz at al. 1992,[8][9]) before being more widely applied in the late 1990s. In cell culture, it has been used to study EGF receptor signaling[10] and ErbB1 receptor trafficking.[11] Time domain FLIM (tdFLIM) has also been used to show the interaction of both types of nuclear intermediate filament proteins lamins A and B1 in distinct homopolymers at the nuclear envelope, which further interact with each other in higher order structures.[12] FLIM imaging is particularly useful in neurons, where light scattering by brain tissue is problematic for ratiometric imaging.[13] In neurons, FLIM imaging using pulsed illumination has been used to study Ras,[14] CaMKII, Rac, and Ran[15] family proteins. FLIM has been used in clinical multiphoton tomography to detect intradermal cancer cells as well as pharmaceutical and cosmetic compounds.

More recently FLIM has also been used to detect flavanols in plant cells[16]

FRET imaging

Since the fluorescence lifetime of a fluorophore depends on both radiative (i.e. fluorescence) and non-radiative (i.e. quenching, FRET) processes, energy transfer from the donor molecule to the acceptor molecule will decrease the lifetime of the donor. Thus, FRET measurements using FLIM can provide a method to discriminate between the states/environments of the fluorophore.[17] In contrast to intensity-based FRET measurements, the FLIM-based FRET measurements are also insensitive to the concentration of fluorophores and can thus filter out artifacts introduced by variations in the concentration and emission intensity across the sample.

Dyes and fluorophores for FLIM

Dye Medium Ab (nm) Em (nm) MW of free Dye QY FLT (ns) Notes
SeTau-380-NHS BSA conjugate, D/P=1 383 468 472 0.44 30.6 Amine-reactive dye
SeTau-405-NHS IgG conjugate, D/P=8 405 518 549 0.19 8.4 Amine-reactive dye
SeTau-405-Maleimide Phosphate buffer pH 7.4 405 518 574 0.51 9.1 Thiol-reactive dye
Seta-633-di-NHS IgG conjugate, D/P=1 639 650 574 0.33 3.0 Amine-reactive dye
SeTau-647 Phosphate buffer pH 7.4 647 693 1400 0.59 3.1 Non-reactive dye
SeTau-647-NHS IgG conjugate, D/P=1 648 694 1400 0.59 3.3 Amine-reactive dye
Square-660-NHS BSA conjugate, D/P=1.2 676 695 574 0.13 3.32 Amine-reactive dye

Abbreviations:
Ab (nm): Absorption wavelength maximum in nanometers
Em (nm): Emission wavelength maximum in nanometers
MW: Molecular weight
QY: Quantum yield
FLT: Fluorescence lifetime in nanoseconds
D/P: Dye-to-protein ratio

See also

References

  1. ↑ Joseph R. Lakowicz. Principles of Fluorescence Spectroscopy 3rd edition. Springer (2006). ISBN 978-0387-31278-1.
  2. ↑ Li, Day-Uei; Arlt, Jochen; Richardson, Justin; Walker, Richard; Buts, Alex; Stoppa, David; Charbon, Edoardo; Henderson, Robert (2010). "Real-time fluorescence lifetime imaging system with a 32 × 32 013μm CMOS low dark-count single-photon avalanche diode array". Optics Express 18 (10): 10257–69. Bibcode:2010OExpr..1810257L. doi:10.1364/OE.18.010257. PMID 20588879.
  3. ↑ Chang, CW; Sud, D; Mycek, MA (2007). "Fluorescence lifetime imaging microscopy". Methods in cell biology. Methods in Cell Biology 81: 495–524. doi:10.1016/S0091-679X(06)81024-1. ISBN 9780123740250. PMID 17519182.
  4. ↑ Elson, D. S.; Munro, I; Requejo-Isidro, J; McGinty, J; Dunsby, C; Galletly, N; Stamp, G W; Neil, M A A; Lever, M J; Kellett, P A; Dymoke-Bradshaw, A; Hares, J; French, P M W (2004). "Real-time time-domain fluorescence lifetime imaging including single-shot acquisition with a segmented optical image intensifier". New Journal of Physics 6: 180. Bibcode:2004NJPh....6..180E. doi:10.1088/1367-2630/6/1/180.
  5. ↑ Sun, Yinghua; Hatami, Nisa; Yee, Matthew; Marcu, Jennifer; Elson, Daniel S.; Gorin, Fredric; Schrot, Rudolph J.; Phipps, Laura (2010). "Fluorescence lifetime imaging microscopy for brain tumor image-guided surgery". Journal of Biomedical Optics 15. Bibcode:2010JBO....15e6022S. doi:10.1117/1.3486612.
  6. ↑ Gadella, T.W.J., editor, FRET and FLIM techniques. Elsevier, 2009 http://books.google.com/books/about/FRET_and_FLIM_Techniques.html?id=uHvqu4hLhH8C&redir_esc=y[]
  7. ↑ Oida, T.; Sako, Y; Kusumi, A (1993). "Fluorescence lifetime imaging microscopy (flimscopy). Methodology development and application to studies of endosome fusion in single cells". Biophysical Journal 64 (3): 676–85. Bibcode:1993BpJ....64..676O. doi:10.1016/S0006-3495(93)81427-9. PMC 1262380. PMID 8471720.
  8. ↑ Lakowicz, Joseph R.; Szmacinski, Henryk; Nowaczyk, Kazimierz; Berndt, Klaus W.; Johnson, Michael (1992). "Fluorescence lifetime imaging". Analytical Biochemistry 202 (2): 316–30. doi:10.1016/0003-2697(92)90112-K. PMID 1519759.
  9. ↑ Lakowicz, Joseph R.; Szmacinski, H; Nowaczyk, K; Johnson, ML (1992). "Fluorescence Lifetime Imaging of Free and Protein-Bound NADH". Proceedings of the National Academy of Sciences of the United States of America 89 (4): 1271–5. Bibcode:1992PNAS...89.1271L. doi:10.1073/pnas.89.4.1271. PMC 48431. PMID 1741380.
  10. ↑ Wouters, Fred S.; Bastiaens, Philippe I.H. (1999). "Fluorescence lifetime imaging of receptor tyrosine kinase activity in cells". Current Biology 9 (19): 1127–30. doi:10.1016/S0960-9822(99)80484-9. PMID 10531012.
  11. ↑ Verveer, Peter J.; Wouters, FS; Reynolds, AR; Bastiaens, PI (2000). "Quantitative Imaging of Lateral ErbB1 Receptor Signal Propagation in the Plasma Membrane". Science 290 (5496): 1567–70. Bibcode:2000Sci...290.1567V. doi:10.1126/science.290.5496.1567. PMID 11090353.
  12. ↑ Delbarre, Erwan; Tramier, Marc; Coppey-Moisan, Maïté; Gaillard, Claire; Courvalin, Jean-Claude; Buendia, Brigitte. "The truncated prelamin A in Hutchinson–Gilford progeria syndrome alters segregation of A-type and B-type lamin homopolymers". Human Molecular Genetics 15 (7): 1113–1122. doi:10.1093/hmg/ddl026.
  13. ↑ Yasuda, Ryohei (2006). "Imaging spatiotemporal dynamics of neuronal signaling using fluorescence resonance energy transfer and fluorescence lifetime imaging microscopy". Current Opinion in Neurobiology 16 (5): 551–61. doi:10.1016/j.conb.2006.08.012. PMID 16971112.
  14. ↑ Harvey, Christopher D.; Yasuda, R; Zhong, H; Svoboda, K (2008). "The Spread of Ras Activity Triggered by Activation of a Single Dendritic Spine". Science 321 (5885): 136–40. Bibcode:2008Sci...321..136H. doi:10.1126/science.1159675. PMC 2745709. PMID 18556515.
  15. ↑ Kaláb, Petr; Soderholm, Jon (2010). "The design of Förster (fluorescence) resonance energy transfer (FRET)-based molecular sensors for Ran GTPase". Methods 51 (2): 220–32. doi:10.1016/j.ymeth.2010.01.022. PMC 2884063. PMID 20096786.
  16. ↑ Mueller-Harvey, Irene; Feucht, Walter; Polster, Juergen; Trnková, Lucie; Burgos, Pierre; Parker, Anthony W.; Botchway, Stanley W. (2012). "Two-photon excitation with pico-second fluorescence lifetime imaging to detect nuclear association of flavanols". Analytica Chimica Acta 719: 68–75. doi:10.1016/j.aca.2011.12.068. PMID 22340533.
  17. ↑ Becker, Wolfgang; Bergmann, Axel (2003). "Lifetime Imaging Techniques for Optical Microscopy" (PDF).

External links

This article is issued from Wikipedia - version of the Thursday, December 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.