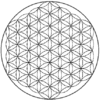
Overlapping circles grid

Example overlapping circle figures

triangular circle grid				square circle grid

An overlapping circles grid is a geometric pattern of repeating, overlapping circles of equal radii in two-dimensional space. The two most common designs are based on circles centered on triangular and square lattice pattern of points.

Patterns of seven overlapping circles appear in historical artefacts from the 8th century BC onwards. They are found on a Cypro-Archaic I cup of the 8th-7th century BC in Cyprus; at the Temple of Osiris at Abydos in Ancient Egypt; and in Roman mosaics, for example at Herod's palace in the 1st century BC. The patterns are used extensively to construct girih decorations including 6- and 12-pointed stars in Islamic art. Patterns based on a square grid of overlapping circles are found in quilt design, in Ancient Egypt as noted in the 1856 book The Grammar of Ornament, and in the Hindu temple at Prambanan in Java.

Triangular grid of overlapping circles

This pattern can be extended to the entire plane, seen here with radial colorings. Progressively larger hexagonal rings contain 1, 7, 19, 37, 61, and 91 circles...

The triangular lattice form is called a seven overlapping circles grid.^[1] It contains 6 circles intersecting at a point, with a 7th circle centered on that intersection.

Overlapping circles with similar geometrical constructions have been used infrequently in various of the decorative arts since ancient times. The pattern has found a wide range of usage in popular culture, in fashion, jewelry, tattoos and decorative products.

Historical occurrences

Five patterns of 19 overlapping circles can be seen on one of the granite columns of the Temple of Osiris in Abydos, Egypt,^[2] and a further five on a column opposite of the building. They are drawn in red ochre and some are very faint and difficult to distinguish.^[3] David Furlong^[4] states that these engravings can date no earlier than 535 BCE and probably date to the 2nd and 4th century CE. His research is based on photographic evidence of Greek text, yet to be fully deciphered. The text is seen alongside the designs and the position close to the top of columns, which are greater than 4 meters in height. Furlong suggests the Osirion was half filled with sand prior to the circles being drawn and therefore likely to have been well after the end of the Ptolemaic dynasty.^[3] The drawings are not mentioned in the extensive listings of graffiti at the temple compiled by Margaret Murray in 1904.^[5]

1, 7, and 19-circle hexagonal variant

In the examples below the pattern has a hexagonal outline, and is further circumscribed.

• 

  1-circle with completed arcs as a Slavic solar symbol

• 

  7-circle: Mosaic floor from a bathhouse in Herod's palace, 1st century BCE

• 

  19-circle symbol with completed arcs inside larger circle

• 

  19-circle: Two symbols drawn in red ochre Temple of Osiris at Abydos, Egypt

• 

  19-circle: A window at the southern apsis of the church of Preveli Monastery (Moni Preveli), Crete.

• 

  19-circle: From Ephesus, Turkey

Similar patterns

In the examples below the pattern does not have a hexagonal outline.

• 

  Drawing by Leonardo da Vinci (Codex Atlanticus, fol. 307v)

• 

  Cup with mythological scenes, a sphinx frieze and the representation of a king vanquishing his enemies. Cypro-Archaic I (8th–7th centuries BC). From Idalion, Cyprus.

• 

  Ball held by the male Imperial Guardian Lion at the Gate of Supreme Harmony, Forbidden City, Beijing, China, showing the geometrical pattern on its surface.

• 

  Floor decoration from the northern Iraq palace of King Ashurbanipal, visible in the Museum of Louvre, dated 645BC.

• 

  A similar overlapping circle pattern: Ayyubid Raqqa ware stoneware glazed jar. Syria, 12th/13th century

Islamic decoration

A girih pattern that can be drawn with compass and straight edge

Window cage at Topkapı Palace, using pattern

In Islamic art, the pattern is one of several arrangements of circles (others being used for fourfold or fivefold designs) used to construct grids for Islamic geometric patterns. It is used to design patterns with 6- and 12-pointed stars as well as hexagons in the style called girih. The resulting patterns however characteristically conceal the construction grid, presenting instead a design of interlaced strapwork.^[6]

Modern usage

19-circle with arcs
Pendant, silver, ⌀ 27 mm
(commercial product, 2013)

Martha Bartfeld, author of geometric art tutorial books, described her independent discovery of the design in 1968. Her original definition said, "This design consists of circles having a 1-[inch] radius, with each point of intersection serving as a new center. The design can be expanded ad infinitum depending upon the number of times the odd-numbered points are marked off." Her subsequent books refer to the design as the Flower of Life, attributed to New Age author Drunvalo Melchizedek.^[7]

Stephen Wolfram's book A New Kind of Science also refers to this pattern as the flower of life from Melchizedek's name for it.^[8] Eric W. Weisstein's book CRC Concise Encyclopedia of Mathematics, Second Edition, also references the pattern and Melchizedek's name.^[9]

The pattern and modern name have propagated into wide range of usage in popular culture, in fashion, jewelry, tattoos and decorative products.

The pattern in quilting has been called diamond wedding ring or triangle wedding ring to contrast it from the square pattern.

Besides an occasional use in fashion,^[10] it is also used in the decorative arts. For example, the album Sempiternal (2013) by Bring Me the Horizon uses the 61 overlapping circles grid as the main feature of its album cover,^[11] whereas the album A Head Full of Dreams (2015) by Coldplay features the 19 overlapping circles grid as the central part of its album cover. Teaser posters illustrating the cover art to A Head Full of Dreams were widely displayed on the London Underground in the last week of October 2015.^[12]

Construction

The pattern figure can be drawn by pen and compass, by creating multiple series of interlinking circles of the same diameter touching the previous circle's center. The second circle is centered at any point on the first circle. All following circles are centered on the intersection of two other circles.

Progressions

The pattern can be extended outwards in concentric hexagonal rings of circles, as shown. The first row shows rings of circles. The second row shows a three-dimensional interpretation of a set of n×n×n cube of spheres viewed from a diagonal axis. The third row shows the pattern completed with partial circle arcs within a set of completed circles.

Expanding sets have 1, 7, 19, 37, 61, 91, 127, etc. circles, and continuing ever larger hexagonal rings of circles. The number of circles is n³-(n-1)³ = 3n²-3n+1 = 3n(n-1)+1.

These overlapping circles can also be seen as a projection of an n-unit cube of spheres in 3-dimensional space, viewed on the diagonal axis. There are more spheres than circles because some are overlapping in 2 dimensions.

Rosette figures including partial circles

1-circle	7-circle (8-1)	19-circle (27-8)	37-circle (64-27)	61-circle (125-64)	91-circle (216-125)	127-circle... (343-216)
1-sphere (1×1×1)	8-sphere (2×2×2)	27-sphere (3×3×3)	64-sphere (4×4×4)	125-sphere (5×5×5)	216-sphere (6×6×6)	343-sphere (7×7×7)
+12 arcs	+24 arcs	+36 arcs	+48 arcs	+60 arcs	+72 arcs	+84 arcs

Other variations

• 

  Richard Kershner showed in 1939 that no arrangement of circles can cover the plane more efficienctly than this hexagonal lattice arrangement^[1]

• 

  Two offset copies of the minimal covering circle pattern (left) make a rhombic tiling pattern, like this red, blue version.

• 

  Three offset copies of the minimal covering circle pattern (left most image) make the 7-circle pattern, like this red, green, blue version.

1. ^ Sphere Packings, Lattices and Groups, John Conway, Neil J. A. Sloane, Chapter 2, section 1.1, Covering space with overlapping circle. pp. 31-32. Figure 2.1 Covering the plane with circles (b) The more efficient or thinner covering in a hexagonal lattice. [1]

Related concepts

Sun of the Alps symbol

The center lens of the 2-circle figure is called a Vesica piscis, from Euclid. Two circles are also called Villarceau circles as a plane intersection of a torus. The areas inside one circle and outside the other circle is called a lune.

The 3-circle figure resembles a depiction of borromean rings and is used in 3-set theory Venn diagrams. Its interior makes a unicursal path called a triquetra. The center of the 3-circle figure is called a reuleaux triangle.

Vesica piscis

Borromean rings

Venn diagram

Triquetra

Reuleaux triangle

The 7-circle pattern has also been called an Islamic seven-circles pattern for its use in Islamic art.

Square grid of overlapping circles

Square lattice form The circle radius is square root of 2 times their separation. A quilt design called a double wedding ring pattern.

Centered square lattice form It can be seen as two half-offset square grids of tangent circles. Egyptian design, from Owen Jones's The Grammar of Ornament (1856)

The square lattice form can be seen with circles that line up horizontally and vertically, while intersecting on their diagonals. The pattern appears slightly different when rotated on its diagonal, also called a centered square lattice form because it can be seen as two square lattices with each centered on the gaps of the other.

It is called a Kawung motif in Indonesian batik, and is found on the walls of the 8th century Hindu temple Prambanan in Java.

It is called a Apsamikkum from ancient Mesopotamian mathematics.^[13]

• 

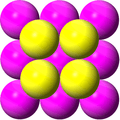
  The square grid can be seen in a face-centered cubic lattice, with 12 spheres in contact around every sphere

• 

  The related five overlapping circles grid is constructed by from two sets of overlapping circles half-offset.^[1]

• 

  Kawung or "Coffee Bean" Batik sarong (detail), Java, Indonesia

1. ^ Creating Square Grids from Circles

See also

• Uniform tiling symmetry mutations - pattern mutations in 3D space
• Knot theory

References

External links

• Weisstein, Eric W., "Circle-circle intersection", MathWorld.

Wikimedia Commons has media related to Flower of Life.