Flippin–Lodge angle

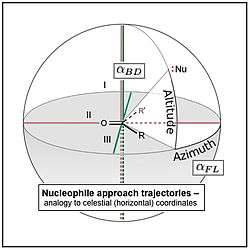
Flippin-Lodge and Bürgi–Dunitz nucleophile approach trajectory angles, and 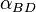, analogized to azimuth and altitude parameters in the celestial (horizontal) coordinate system.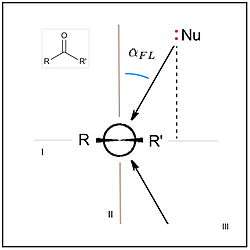

Flippin-Lodge angle, , for a nucleophilic "attack" (addition) at a carbonyl-containing electrophile, in Newman projection, with electrophile plane I viewed edge-on.^[1]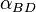

Both in this celestial coordinate system, and in the system to describe a nucleophile approaching a planar electrophile, the problem is to uniquely describe the location of a point off of a plane, relative to specific point on the plane. Hence, in both cases, the problem can be addressed using two angles, an altitude-type angle and an azimuth-type angle. Note, while elevation in celestial applications is most easily measured as the specific altitude shown, the elevation of the nucleophile, , is most easily measured as the supplementary angle, Nu-C-O, hence its values are most often >90° (see text).

The Flippin–Lodge angle is one of two angles used by organic and biological chemists studying the relationship between a molecule's chemical structure and ways that it reacts, for reactions involving "attack" of an electron-rich reacting species, the nucleophile, on an electron-poor reacting species, the electrophile. Specifically, the angles—the Bürgi–Dunitz, 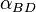, and the Flippin–Lodge, —describe the "trajectory" or "angle of attack" of the nucleophile as it approaches the electrophile, in particular when the latter is planar in shape. This is called a nucleophilic addition reaction and it is plays a central role in the biological chemistry taking place in many biosyntheses in nature, and is a central "tool" in the reaction toolkit of modern organic chemistry, e.g., to construct new molecules such as pharmaceuticals. Theory and use of these angles falls into the area of physical organic chemistry, which deals with chemical structure and reaction mechanism, and within a sub-specialty called structure correlation.

Because chemical reactions take place in three dimensions, their quantitative description is, in part, a geometry problem. Two angles, first the Bürgi–Dunitz angle, 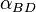, and later the Flippin–Lodge angle, , were developed to describe the approach of the reactive atom of a nucleophile (a point off of a plane) to the reactive atom of an electrophile (a point on a plane). The is an angle that estimates the displacement of the nucleophile, at its elevation, toward or away from the particular R and R' substituents attached to the electrophilic atom (see image). The 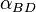is the angle between the approach vector connecting these two atoms and the plane containing the electrophile (see the Bürgi–Dunitz article). Reactions addressed using these angle concepts use nucleophiles ranging from single atoms and polar organic functional groups to chiral catalyst reaction systems, to complex enzyme active site. These nucleophiles can be paired with an array of planar electrophiles: aldehydes and ketones, carboxylic acid-derivatives, and the carbon-carbon double bonds of alkenes (olefins). Studies of 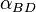and can be theoretical, based on calculations, or experimental (either quantitative, based on X-ray crystallography, or inferred and semiquantitative, rationalizing results of particular chemical reactions), or a combination of these.

The most prominent application and impact of the Flippin-Lodge angle has been in the area of chemistry where it was originally defined: in practical synthetic studies of the outcome of carbon-carbon bond-forming reactions in solution. An important example is the aldol reaction, e.g., addition of ketone-derived nucleophiles (enols, enolates), to electrophilic aldehydes that have attached groups varying in size and polarity. Of particular interest, given the three-dimensional nature of the concept, is understanding how features on the nucleophile and electrophile impact the stereochemistry of reaction outcomes (i.e., the "handedness" of new chiral centers created by a reaction). Studies invoking Flippin-Lodge angles in synthetic chemistry have improved the ability of chemists to predict outcomes of known reactions, and to design better reactions to produce particular stereoisomers (enantiomers and diastereomers) needed in the construction of complex natural products and drugs.

Technical introduction

The Flippin–Lodge (FL) angle, is the latter-derived of two angles that fully define the geometry of "attack" (approach via collision) of a nucleophile on an trigonal unsaturated center of an electrophilic molecule. Nucleophiles in this addition reaction may range from single atoms (hydride, chloride), to polar organic functional groups (amines, alcohols), to complex systems (nucleophilic enolates with chiral catalysts, amino acid side chains in enzyme active sites; see below). Planar electrophiles include aldehydes and ketones, carboxylic acid-derivatives such as esters, and amides, and the carbon-carbon double bonds of particular alkenes (olefins).^[2][1] In the example of nucleophilic attack at a carbonyl, is a measure of the "offset" of the nucleophile's approach to the electrophile, toward one or the other of the two substituents attached to the carbonyl carbon.^[3][2][1] The relative values of angles for pairs of reactions can be inferred and semiquantitative, based on rationalizations of the products of the reactions; alternatively, as noted in the figure, values may be formally derived from crystallographic coordinates by geometric calculations, or graphically, e.g., after projection of Nu onto the carbonyl plane and measuring the angle supplementary to LNu'-C-O (where Nu' is the projected atom). This often overlooked angle of the nucleophile's trajectory was named the Flippin-Lodge angle by Clayton H. Heathcock after his contributing collaborators Lee A. Flippin and Eric P. Lodge.^[1][4][5][3] The second angle defining the geometry, the more well known Bürgi–Dunitz angle, 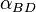, describes the Nu-C-O bond angle and was named after crystallographers Hans-Beat Bürgi and Jack D. Dunitz, its first senior investigators (see related article).^[6]

The Flippin-Lodge angle has been abbreviated variously by the symbols φ, ψ, θ_x, and or ;^{[2][3][7][6][8]} the latter pair to closely associate the Flippin-Lodge angle with its sister angle, the Bürgi–Dunitz, which was originally abbreviated as by its discoverers/formulators (e.g., see Bürgi ey al., 1974.^[6]). The symbols and 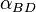will be used here, respectively, to refer to the Flippin-Lodge and Bürgi-Dunitz concepts and measured values.

Angle as experimental observable

These angles are best construed to mean the angles observed/measured for a given system, and not an historically observed range in values (e.g., the 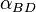range of the original Bürgi–Dunitz aminoketones), or an idealized value computed for a particular system (such as the = 0° for hydride addition to formaldehyde).^[6] That is, the 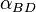and angles of the hydride-formadehyde system have one pair of values, while the angles observed for other systems are fully expected to vary from this.^[2][7]

A stated convention for is that it is positive when deviating in the direction away from the larger substituent attached to the electrophilic center, or away from the more electron-rich substituent (where these two and other factors can be in a complex competition, see below); of a symmetrically substituted carbonyl (R = R') with a simple nucleophile is expected to be 0° in vacuo / in solutio, e.g., as in the case of hydride addition to formaldehyde, H₂C=O.^[2]

Steric and orbital contributions to its value

In contrast to 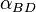,^[6] and using the case of carbonyl additions as example: the angle adopted during an approach by the nucleophile to a trigonal electrophile depends in complex fashion on:

• the relative steric size of the two substituents attached to (alpha to) the electrophilic carbonyl, which give rise to varying degrees of repulsive van der Waals's interactions (e.g., giving ≈ 7° for pivaldehyde, R=tertiary-butyl, and R'=H),^[2]
• the electronic characteristics of substituents alpha to the carbonyl, where heteroatom-containing substituents can, through their stereoelectronic influence, function as overly intrusive steric groups (e.g., giving ≈ 40-50° for esters and amides with small R' groups, since R is an O- and N-substituent, respectively),^[2] and
• the nature of the bonds made by more distant atoms to the atoms alpha to the carbonyl, e.g., where the energy of the σ* molecular orbital (MO) between the alpha- and beta-substituents was seen to compete with the foregoing influences,^[4]

as well as on the MO shapes and occupancies of the carbonyl and attacking nucleophile.^[2][3] Hence, the 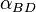observed for nucleophilic attack appears to be influenced primarily by the energetics of the HOMO-LUMO overlap of the nucleophile-electrophile pair in the systems studied—see the Bürgi–Dunitz article, and the related inorganic chemistry concept of the angular overlap model^[9][10][11]—which leads in many cases to a convergence of 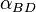values (but not all, see below); however, the required to provide optimal overlap between HOMO and LUMO may reflect a more complex interplay of energetic contributions.

Origin and current scope of concept

Bürgi–Dunitz angle theory was initially developed based on "frozen" interactions in crystals, while most chemistry takes place via collisions of molecules tumbling in solution; remarkably, the theories of the , with the complexity they reflect, evolved from studying reaction outcomes in such practical reactions as addition of enolates to aldehydes (e.g., in study of diastereoselection in particular aldol reactions).^[1][3] In applying both angles of the nucleophile trajectory to real chemical reactions, the HOMO-LUMO centered view of the BD angle is modified to include further complex, electrophile-specific attractive and repulsive electrostatic and van der Waals interactions that can alter the BD angle and bias toward one substituent or the other (see above).^[4] As well, dynamics at play in each system (changing torsional angles) are implicitly included in studies of reaction outcomes in solution as in the early studies of ,^[4] though not in crystallographic structure correlation approaches as gave birth to the BD concept. Finally, in constrained environments (e.g., in enzyme and nanomaterial binding sites) observed angles appear to be quite distinct, an observation conjectured to arise because reactivity is not based on random collision, and so the relationship between orbital overlap principles and reactivity is more complex.^[7][12] For instance, while a simple amide addition study with relatively small substituents gave an of ≈50° in solution,^[2] the crystallographic value determined for an enzymatic cleavage of an amide by the serine protease subtilisin gave an of 8°, and a compilation of literature crystallographic values for the same reaction in different catalysts clustered at 4 ± 6° (i.e., only slightly offset from directly behind the carbonyl, despite significant dissymmetry of the substrate electrophiles).^[7] At the same time, the subtilisin 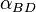was 88° (quite distinct from the hydride-formaldehyde 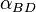value of 107°, see the Bürgi–Dunitz article), and 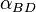angle values from the careful compilation clustered at 89 ± 7° (i.e., only slightly offset from directly above or below the carbonyl carbon).

Applications

The Flippin-Lodge and Bürgi-Dunitz angles were central, practically, to the development of a clearer understanding of asymmetric induction during nucleophilic attack at hindered carbonyl centers in synthetic organic chemistry. It was in this area that was first defined by Heathcock, and has been primarily used.^[1][3] Larger substituents around the electrophilic center, such as tert-butyls, lead to higher stereoselectivities in asymmetric induction than smaller substituents like methyls. The trajectory of the nucleophile approaching a center flanked by two large substituents is more limited, i.e. the Flippin-Lodge angle is smaller. For example, in Mukaiyama aldol addition, the bulkier phenyl tert-butyl ketone has a higher selectivity for the syn isomer than the smaller phenyl methyl ketone. Likewise, if bulky a nucleophile, such as a t-butylmethylsilyl enolate, is used, the selectivity is higher than for a small nucleophile like a lithium enolate.^[5]

Given a reaction system of a given nucleophile with a carbonyl having the two substituents R and R', where substituent R' is sterically small relative to substituent R (e.g., R' = hydrogen atom, R = phenyl), the values that are inferred from the reaction outcomes and theoretical studies tend to be larger; alternatively, if the hydrocarbon substituents are nearer or equal in steric size, the inferred values diminish and may approach zero (e.g., R' = tert-butyl, R = phenyl). Thus, from the perspective of simpler electrophile systems where only steric bulk come into play, the attack trajectories of the classes of nucleophiles studied makes clear that as the disparity in size between the substituent increase, there is a perturbation in the FL angle that can be used to provide higher stereoselectivities in designed reaction systems; while the patterns become more complex when factors other than steric bulk come into play (see section above on orbital contributions),^[4][2] Flippin, Lodge, and Heathcock were able to show that generalizations could be made that were useful to reaction design.^[3][2][1]

A surpassing area of application has been in studies of various aldol reactions, the addition of ketone-derived enol/enolate nucleophiles to electrophilic aldehydes, each with functional groups varying in size and group polarity;^[3] the way that features on the nucleophile and electrophile impact the stereochemistry seen in reaction products, and in particular, the diastereoselection exhibited, has been carefully mapped (see the steric and orbital description above,^[1][2][3] the aldol reaction article, and David Evans' related Harvard teaching materials on the aldol^[13]). These studies have improved the chemists' abilities to design enantioselective and diastereoselective reactions needed in the construction of complex molecules, such as the natural product spongistatins^[14] and modern drugs.^[15][16] It remains to be seen whether a particular range of values contributes similarly to the arrangement of functional groups within proteins and so to their conformational stabilities (as has been reported in relation to the BD trajectory),^[17][18] or to other BD-correlated stabilizations of conformation important to structure and reactivity.^[19]

References

Further reading

• Heathcock, C.H. (1990) Understanding and controlling diastereofacial selectivity in carbon-carbon bond-forming reactions, Aldrichimica Acta 23(4):94-111, esp. p. 101, see , accessed 5 January 2014.
• Mahrwald, Rainer (1999). "Diastereoselection in Lewis-Acid-Mediated Aldol Additions" (PDF). Chem. Rev. 99: 1095−1120, esp. pp. 1099, 1102, 1108. Retrieved 5 December 2015. 
• Evans, D.A., et al. (2006) "Carbonyl and Azomethine Electrophiles [Lectures 21, 22]," Chemistry 206, Advanced Organic Chemistry, packet pp. 91-99, 106-110, and 116, Cambridge, MA, USA:Harvard University Chemistry Department, see , accessed 5 December 2015.
• Fleming, Ian (2010) Molecular Orbitals and Organic Chemical Reactions: Reference Edition, John Wiley and Sons, pp. 214–215. ISBN 0470746580, see , accessed 5 January 2014.

See also

• Bürgi–Dunitz angle